Codeforces Round #249 (Div. 2) D. Special Grid （递推乱搞）（好题）

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an n × m grid, some of its nodes are black, the others are white. Moreover, it's not an ordinary grid — each unit square of the grid has painted diagonals.

The figure below is an example of such grid of size 3 × 5. Four nodes of this grid are black, the other 11 nodes are white.

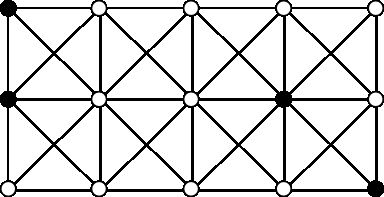
Your task is to count the number of such triangles on the given grid that:

• the corners match the white nodes, and the area is positive;
• all sides go along the grid lines (horizontal, vertical or diagonal);
• no side contains black nodes.

Input

The first line contains two integers n and m (2 ≤ n, m ≤ 400). Each of the following n lines contain m characters (zeros and ones) — the description of the grid. If the j-th character in the i-th line equals zero, then the node on the i-th horizontal line and on the j-th vertical line is painted white. Otherwise, the node is painted black.

The horizontal lines are numbered starting from one from top to bottom, the vertical lines are numbered starting from one from left to right.

Output

Print a single integer — the number of required triangles.

Sample test(s)

input

3 5
10000
10010
00001

output

20

input

2 2
00
00

output

4

input

2 2
11
11

output

0

Note

The figure below shows red and blue triangles. They are the examples of the required triangles in the first sample. One of the invalid triangles is painted green. It is invalid because not all sides go along the grid lines.

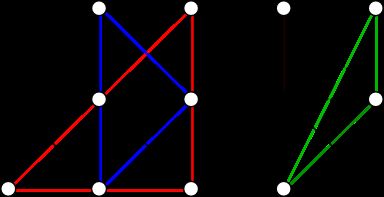
大致题意：

400*400的黑白网格，

求出有多少个三角形满足：

1.三边必须是网格上的线

2.三边上均不存在黑点

思路：

显然复杂度要在n^3以内

这题比较开放，观察图形特点，然后去解决就好

我的思路是，从四个方向递推，维护底边的合法性，然后O（n）求出以(x,y)为底边中点的合法三角形个数

过程中要O(1)判出某条斜边上是否存在黑点，可以用前缀和解决，斜边必然是45度或者135度的，所以用sun[n][m][2]，维护两个斜向的前缀和即可

//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <string>
#include <vector>
#include <cstdio>
#include <ctime>
#include <bitset>
#include <algorithm>
#define SZ(x) ((int)(x).size())
#define ALL(v) (v).begin(), (v).end()
#define foreach(i, v) for (__typeof((v).begin()) i = (v).begin(); i != (v).end(); ++ i)
#define reveach(i, v) for (__typeof((v).rbegin()) i = (v).rbegin(); i != (v).rend(); ++ i)
#define REP(i,n) for ( int i=1; i<=int(n); i++ )
#define rep(i,n) for ( int i=0; i<int(n); i++ )
using namespace std;
typedef long long ll;
#define X first
#define Y second
typedef pair<ll,ll> pii;

template <class T>
inline bool RD(T &ret) {
	char c; int sgn;
	if (c = getchar(), c == EOF) return 0;
	while (c != '-' && (c<'0' || c>'9')) c = getchar();
	sgn = (c == '-') ? -1 : 1;
	ret = (c == '-') ? 0 : (c - '0');
	while (c = getchar(), c >= '0'&&c <= '9') ret = ret * 10 + (c - '0');
	ret *= sgn;
	return 1;
}
template <class T>
inline void PT(T x) {
	if (x < 0) {
		putchar('-');

		x = -x;
	}
	if (x > 9) pt(x / 10);
	putchar(x % 10 + '0');
}

const int inf = 0x3f3f3f3f;
const int N = 400+100;
char mp[N][N];
int sum[N][N][2];
int n,m;



inline bool ok(int x,int y,int a,int b){
        if( x > a ) swap(x,a),swap(y,b);
        if( x < a && y < b) return ( sum[a][b][0]-sum[x-1][y-1][0] == 0 );
        return (sum[x][y][1]-sum[a+1][b-1][1] == 0);
}
inline bool judge(int x,int y){
        return ( x >= 1 && x <= n && y >= 1 && y <= m && mp[x][y] == '0');
}

int main(){
        cin>>n>>m;
        REP(i,n) scanf("%s",mp[i]+1);

        REP(i,n) REP(j,m) sum[i][j][0] = sum[i-1][j-1][0]+( mp[i][j] == '1' );
        rep(i,n) REP(j,m) sum[n-i][j][1] = sum[n-i+1][j-1][1]+( mp[n-i][j] == '1' );

        int ans = 0;
        REP(x,n) REP(y,m){
                if( mp[x][y] == '1' ) continue;
                bool ok1 = 1, ok2 = 1;
                REP(d,inf){
                        if( !ok1 && !ok2 ) break;
                        if( ok1 ) ok1 = judge(x,y-d) && judge(x-d,y);
                        if( ok2 ) ok2 = judge(x,y+d) && judge(x-d,y);
                        ans += ok1 && ok(x,y-d,x-d,y);
                        ans += ok2 && ok(x,y+d,x-d,y);
                }
                ok1 = ok2 = 1;
                REP(d,inf){
                        if( !ok1 && !ok2 ) break;
                        if( ok1 ) ok1 = judge(x,y-d) && judge(x+d,y);
                        if( ok2 ) ok2 = judge(x,y+d) && judge(x+d,y);
                        ans += ok1 && ok(x,y-d,x+d,y);
                        ans += ok2 && ok(x,y+d,x+d,y);
                }
        }

        REP(x,n) REP(y,m){
                if( mp[x][y] == '1' ) continue;
                bool flag = 1;
                REP(d,inf){
                        if( !flag ) break;
                        flag = judge(x,y-d) && judge(x,y+d) && (x-d >= 1);
                        ans += flag && ok(x,y-d,x-d,y) && ok(x,y+d,x-d,y);
                }
                flag = 1;
                REP(d,inf){
                        if( !flag ) break;
                        flag = judge(x,y-d) && judge(x,y+d) && (x+d <= n);
                        ans += flag && ok(x,y-d,x+d,y) && ok(x,y+d,x+d,y);
                }
                flag = 1;
                REP(d,inf) {
                        if( !flag ) break;
                        flag = judge(x-d,y) && judge(x+d,y) && (y-d >=1);
                        ans += flag && ok(x-d,y,x,y-d) && ok(x+d,y,x,y-d);
                }
                flag = 1;
                REP(d,inf){
                        if( !flag ) break;
                        flag = judge(x-d,y) && judge(x+d,y) && (y+d <= m);
                        ans += flag && ok(x-d,y,x,y+d) && ok(x+d,y,x,y+d);
                }
        }
        printf("%d\n",ans);
}