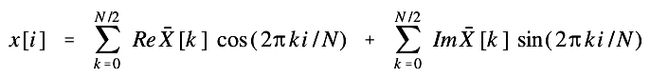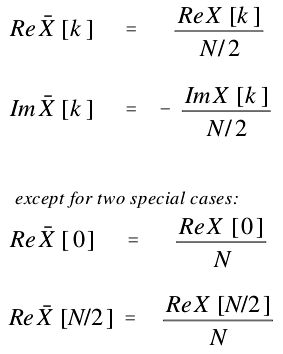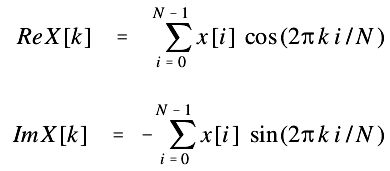离散傅立叶变换（Discrete Fourier Transform）

离散傅立叶变换概述

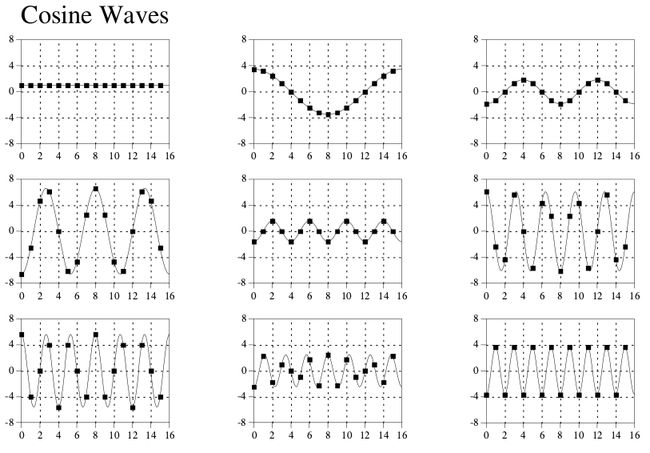
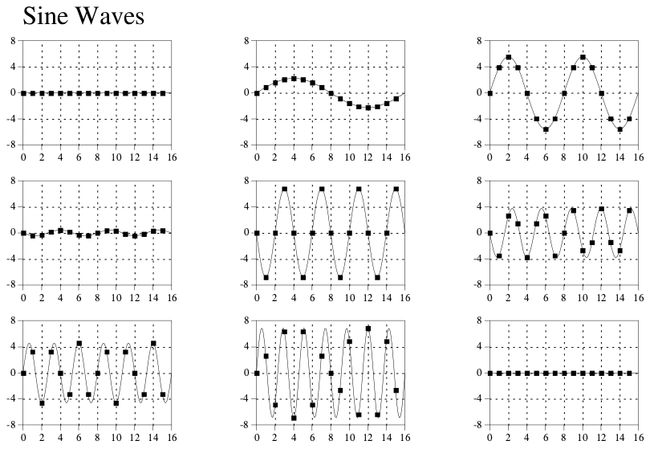
傅立叶分析以法国数学家和物理学家JeanBaptiste JosephFourier命名，是一种将信号分解为谐波的方法。如下三图所示，一个包含16个点的离散信号可以用9个余弦和9个正弦波来表示。在表达任意一个离散信号时，这些三角波的周期是一定的，不同的只是振幅(amplitude)。

图 1-1 离散信号与对应的三角波

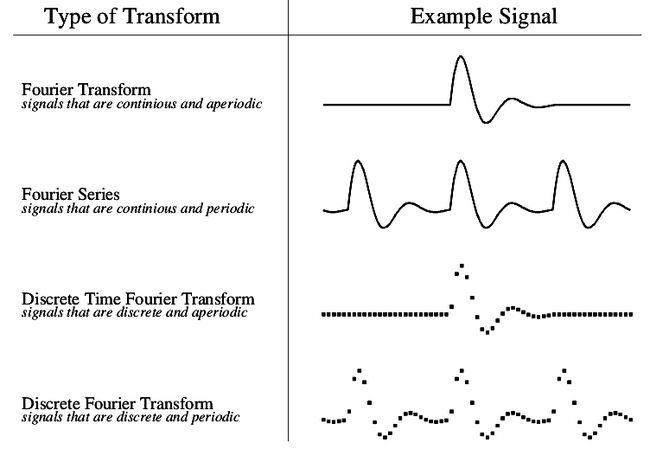
信号可以是连续的或离散的，同时也可以是周期性的或非周期性的，根据信号的这两个特点，傅立叶变换可以分为四种类型：

傅立叶变换（FourierTransform），处理非周期性的连续信号（Aperiodic-Continuous）。

傅立叶序列(FourierSeries)，处理周期性的连续信号（Periodic-Continuous）。

离散时间域傅立叶变换（DiscreteTime Fourier Transform），处理非周期性的离散信号（Aperiodic-Discrete）。

离散傅立叶变换(DiscreteFourier Transform)，处理周期性的离散信号(Periodic-Discrete)。

计算机只能处理离散的和有限长度的信号，因此只有离散傅立叶变换(DFT)能在计算机中以算法实现。

图1-2 四种不同类型的傅立叶分析

实数离散傅立叶变换（RealDFT）的格式和表示

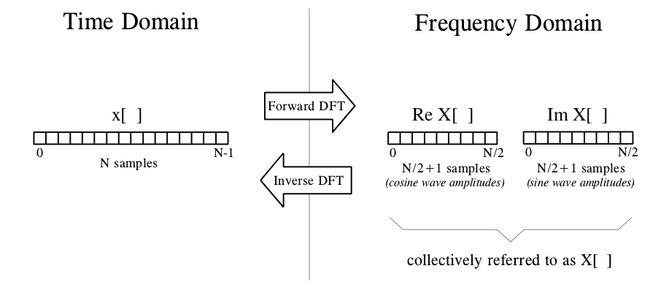
如图1-3所示，离散傅立叶变换将包含N个点的输入波转为两个包含N/2+1个点的输出波。输入波常被称作时间域，因为信号的波形基本上都是随时间变化，输出波常被称作频率域。

时间域与频率域中存储的信息是一样的，只是表现方式不一样。将时间域转为频率域的过程叫离散傅立叶变换（DFT），将频率域转换为时间域的过程叫反变换（IDFT）。频率域可以分为两部分，实数部分ReX[ ]和虚数部分Im X[]，分别存放余弦函数(Cosine)的振幅和正弦函数(Sine)的振幅。

图 1-3 实数傅立叶变换示意图

DFT基函数

DFT中使用的正弦和余弦函数统称为基函数(BasisFunction)，这些三角函数的周期是固定的，变化的只是振幅。DFT基函数的表达式：

C_k[i]= cos(2ki/N)

S_k[i]= sin(2ki/N)

公式1-1

其中，C_k[i]和S_k[i]表示由N个点组成的离散正弦曲线，i的取值范围是张倒N-1。k决定了曲线的周期，取值范围是0到N/2。

多余的系数

完成DFT后，系数由原来的N个变为N+2个，似乎产生了两个多余的系数。在频率域中，的确有两个系数是多余的，它们是ImX[0]和ImX[n/2]。它们的存在使得频率域中的其他系数相互独立，并且它们的值永远为0，因此不会影响反变换。

反变换的计算(IDFT)

公式1-2

在上面的公式中，振幅使用的是和，而不是ImX[k]和ReX[k]。两者的关系可以用下面的公式来表示：

公式1-3

反变换的算法实现

下面是反变换算法的伪代码实现：

100'THE INVERSE DISCRETE FOURIER TRANSFORM

110'The time domain signal, held in XX[ ], is calculated from thefrequency domain signals,

120'held in REX[ ] and IMX[ ].

130'

140DIM XX[511] 'XX[ ] holds the time domain signal

150DIM REX[256] 'REX[ ] holds the real part of the frequency domain

160DIM IMX[256] 'IMX[ ] holds the imaginary part of the frequency domain

170'

180PI = 3.14159265 'Set the constant, PI

190N% = 512 'N% is the number of points in XX[ ]

200'

210GOSUB XXXX 'Mythical subroutine to load data into REX[ ] and IMX[ ]

220'

230

240''Findthe cosine and sine wave amplitudes using Eq. 1-3

250FOR K% = 0 TO 256

260REX[K%] = REX[K%] / (N%/2)

270IMX[K%] = -IMX[K%] / (N%/2)

280NEXT K%

290'

300REX[0] = REX[0] / 2

310REX[256] = REX[256] / 2

320'

330'

340FOR I% = 0 TO 511 'ZeroXX[ ] so it can be used as an accumulator

350XX[I%] = 0

360NEXT I%

370'

380'Eq. 1-2 SYNTHESIS METHOD #1. Loop through each

390'frequency generating the entire length of the sine and cosine

400'waves, and add them to the accumulator signal, XX[ ]

410'

420FOR K% = 0 TO 256 'K% loops through each sample in REX[ ] and IMX[ ]

430FOR I% = 0 TO 511 'I% loops through each sample in XX[ ]

440'

450XX[I%] = XX[I%] + REX[K%] * COS(2*PI*K%*I%/N%)

460XX[I%] = XX[I%] + IMX[K%] * SIN(2*PI*K%*I%/N%)

470'

480NEXT I%

490NEXT K%

500'

510END

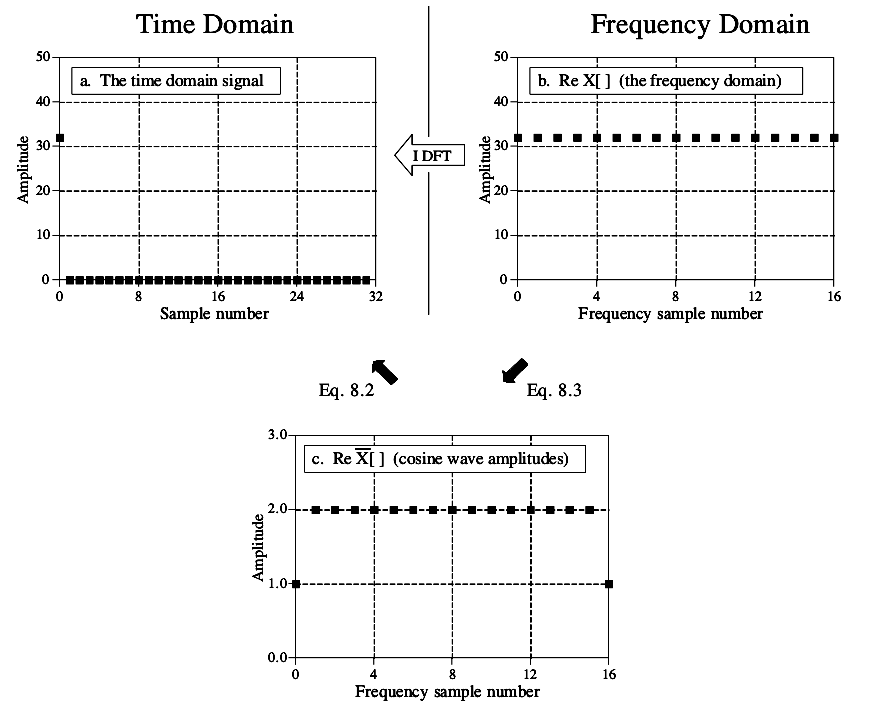
图1-4 IDCT示意图

图1-4解释了IDCT的过程以及频率域与反变换时振幅的不同。图1-4a中是我们需要进行转换的时间域曲线，在0点坐标处振幅为32的一条曲线；图1-4b是进行DFT变换后的曲线，实数部分（ReX）的值为32，虚数部分的值全部为0，因此这里没有画虚数部分的曲线；公式1-3将频率域信号（图1-4b所示）转换为余弦函数的振幅（图1-4c所示）。虚数部分（用正弦函数表示）的系数全部为0，因此这里没有显示。

频率域与三角函数振幅之所以不同，是因为频率域被定义为谱密度（spectraldensity）。

图1-4显示的是一个由32个点组成的信号在频率域中的实数部分，由编号从0到16的17个采样点组成。谱密度是指单位带宽所能表达的信号量（振幅），其计算方法是使用三角函数的振幅除以相应的带宽（bandwidth）。

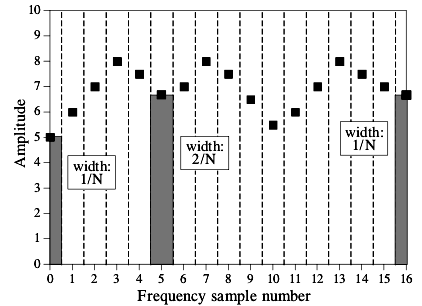
图1-4中的虚线解释了带宽的计算，即在采样点之间进行平均分割。采样点0和16的带宽为1/N，其他采样点（1-15）的带宽为2/N。这就是公式1-3中ReX[0]和ReX[N/2]与其他ReX不同的原因。

图 1-5频率域的带宽(bandwidth)

DFT的分析与计算

DFT的计算有三种方法：第一种是解线性方程祖，这种方法简单但计算量很大，实际应用中很少使用；第二种是关联法（correlation），基于已知的另一条的曲线；第三中方法是快速傅立叶变换（FFT），FFT算法将对一条含N个点曲线的计算转为对N条含1个点的曲线的计算，从而大大降低了计算量。

线性方程组求解DFT

使用这种方法来计算DFT是很自然的，从N个方程求解N个未知数。但这种方法计算量很大，实际应用中很少使用。

关联法（correlation）求解DFT

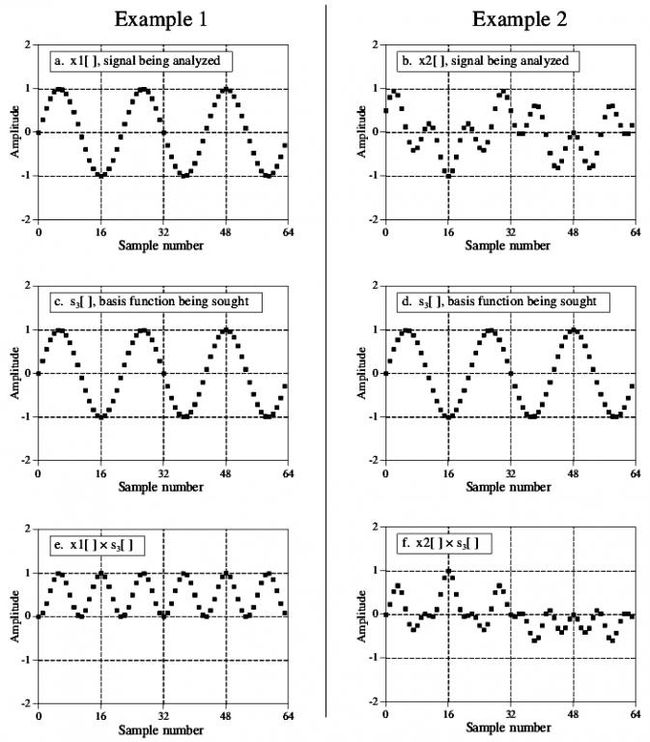
通过correlation求解DFT是求解DFT的标准方法，下面使用一个例子来说明这种方法。求解一个包含64个点的信号的DFT，意味着我们要计算频率域中实数部分的33个系数和虚数部分的33个系数。在这个例子中，我们只解一个系数，ImX[3]。

ImX[3]是一条包含三个完整周期的正弦函数的振幅，这个正弦函数曲线分布在点0到点63之间，如图1-6a所示。

在图1-6中，a和b是两个时间域的示例信号，在这里分别称之为x1[]和x2[]。曲线x1[]是一个包含3个完整周期、分布在0到63之间的正弦函数曲线；x2[]由多条正弦函数曲线和余弦函数曲线混合而成，在组成x2[]的三角函数曲线中，没有任何一条在0到63之间有完整的三个周期。

通过这两条曲线可以解释算法要实现的功能：当输入函数为x1[]时，算法的计算结果应该是32，也就是信号中正弦曲线的振幅；而当输入函数为x2[]时，算法的计算结果应该为0，因为x2[]所表示的曲线并不在这个信号中。

之所以非x1[]的曲线与x1[]相乘结果为0，是因为除x1[]外的任意一个函数与正弦函数相乘时，在0到63（3个完整周期）上的积分都为0。在图1-6中，图e是图a和图c相乘的结果，将各个点的值相加即可得到32；图f是图b和图d相乘的结果，将各个点的值相加得到的结果为0。

上面的计算过程可以用公式1-4来表示。

公式1-4

图1-6关联法（correlation）求DFT

下面是关联法计算DFT的算法伪代码：

100'THE DISCRETE FOURIER TRANSFORM

110'The frequency domain signals, held in REX[ ] and IMX[ ], are calculatedfrom

120'the time domain signal, held in XX[ ].

130'

140DIM XX[511] 'XX[ ] holds the time domain signal

150DIM REX[256] 'REX[ ] holds the real part of the frequency domain

160DIM IMX[256] 'IMX[ ] holds the imaginary part of the frequency domain

170'

180PI = 3.14159265 'Set the constant, PI

190N% = 512 'N% is the number of points in XX[ ]

200'

210GOSUB XXXX 'Mythical subroutine to load data into XX[ ]

220'

230'

240FOR K% = 0 TO 256 'Zero REX[ ] & IMX[ ] so they can be used as accumulators

250REX[K%] = 0

260IMX[K%] = 0

270NEXT K%

280'

290' 'Correlate XX[ ] with the cosine and sine waves, Eq. 8-4

300'

310FOR K% = 0 TO 256 'K% loops through each sample in REX[ ] and IMX[]

320FOR I% = 0 TO 511 'I% loops through each sample in XX[ ]

330'

340REX[K%] = REX[K%] + XX[I%] * COS(2*PI*K%*I%/N%)

350IMX[K%] = IMX[K%] - XX[I%] * SIN(2*PI*K%*I%/N%)

360'

370NEXT I%

380NEXT K%

390'

400END

二元性（Duality）

DFT和IDFT变换公式很类似。从一个域到另一个域，都是用已有的值乘以基函数，然后将相应的值相加。实际上，DFT和IDFT的区别仅仅是时间域中包含N个点，而频率域中包含N/2+1个点。在复数傅里叶变换中，时间域和频率域中的信号都包含N个点，这使得两个域具有一种对称的性质，而在两个域之间的转换公式也就几乎一样了。

时间域和频率域的这种对称被称之为对称性（Duality），二元性可以产生很多有趣的性质。例如：在频率域中的一个单点对应于时间域中的一条三角函数曲线，由于Duality，这种性质反过来也成立，在时间域中的一个点对应于频率域中的一条三角函数曲线。