入门二叉平衡树的世界

入门二叉平衡树的世界

1. 二叉平衡树的概念

    二叉平衡树又称AVL树，它或者是一棵空二叉树，或者是具有下列性质的二叉树：

1） 根的左右子树高度之差的绝对值不超过1；

2） 根的左右子树都是二叉平衡树。

二叉树上节点的平衡因子定义为该节点的左子树的高度减去右子树的高度，故AVL树的所有节点的平衡因子只可能是-1、0、1. 

    二叉平衡树是一种特殊的二叉搜索树，能够控制树的高度，避免产生普通二叉搜索树的退化树形。AVL树是对二叉搜索树的一种改进，二叉搜索树的缺点就是：树的结构是无法预料的，随意性很大，它只与节点的值和插入的顺序有关系，往往得到的是一个不平衡的二叉树。在最坏的情况下，可能得到的是一个单支二叉树，其高度和节点数相同，相当于单链表，对其正常的查找的时间复杂度就不是O(log n)，而是O(n),也就丧失了二叉搜索树的一些应有的优点。

    当插入一个新的节点的时候，在普通的二叉树中不同考虑树的平衡因子，只要将大于根节点的值插入到右子树，小于节点的值插入到左子树，递归即可。但是，AVL树在插入节点的时候，如果插入节点之后有一个节点的平衡因子要大于或者小于-2的时候，需要进行调整。

2. 二叉平衡树的4种调整方式

    二叉平衡树中最复杂的就要数4种调整方式了：LL、RR、LR和RL。对二叉平衡树的插入和删除，在每次插入和删除一个节点之后都有可能破坏其平衡性，此时就需要调整。这点和建立最大堆和最小堆是一致的思想。下面我们就详细介绍一下如何实现这4种调整：

    在介绍调整之前，需要理解最小不平衡子树的概念：如果在插入节点前，从根节点到新节点插入位置的路径上的所所有节点的平衡因子bf均为0，那么插入后这棵树仍然是二叉平衡树，而高度加1；如果在这条路径上，某个节点（设由指针s指示）的平衡因子不为0，但自它以下直至新节点的所有节点的平衡因子原先都为0，那么插入后，以节点s为根节点的子树就有可能是最小不平衡子树。我们调整的范围业绩是这棵最小不平衡子树。

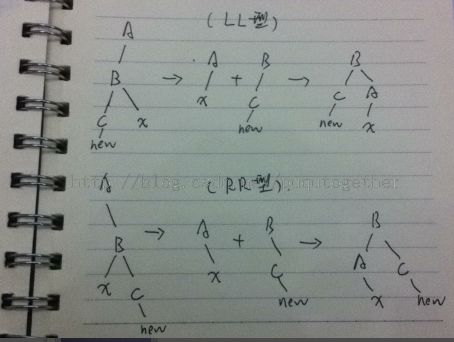
1）LL型调整：

LL型就是在A节点的左子树B的左子树C上插入新节点new。调整的步骤为：

step 1：B节点作为新的节点，那么就需要把B的右子树x给A的左子树；

step 2：B节点为左子树，那么右子树即为A，把A给B的右子树；

step 3：A和B的平衡因子设置0，C的平衡因子不变；

2）RR型调整：

RR型就是在A右子树B的右子树C插入一个新节点new，调整的步骤如下：

step 1：B作为新的根节点，先把B的左子树x赋给A的右子树；

step 2：因为B是新的根节点，C为B的右子树，把A赋给B的左子树；

step 3：A和B的平衡因子为0，C的平衡因子不变；

3）LR型调整：

LR型就是在A左子树B的右子树C插入一个新节点，调整的步骤如下：

step 1：C作为新的根节点；

step 2：先把C的右子树CR赋给A的左子树，C的左子树CL赋给B的右子树；

step 3：再把B作为C的左子树，A作为C的右子树，C作为新的根节点；

step 4：如果原先C的平衡因子bf=1，则A的新bf为-1，B的新bf为0；

             如果原先C的平衡因子bf=-1，则A的新bf为0，B的新bf为1；

             如果原先C的平衡因子bf=0，则A的新bf为0，B的新bf为0；

4）RL型调整：

RL型就是在A右子树B的左子树C插入一个新节点，调整的步骤如下：

step 1：C作为新的根节点；

step 2：先把C的右子树CR赋给B的左子树，C的左子树CL赋给A的右子树；

step 3：再把A作为C的左子树，B作为C的右子树，C作为新的根节点；

step 4：如果原先C的平衡因子bf=1，则A的新bf为0，B的新bf为-1；

             如果原先C的平衡因子bf=-1，则A的新bf为1，B的新bf为0；

             如果原先C的平衡因子bf=0，则A的新bf为0，B的新bf为0；

插入节点的代码如下：（网上复制的，自己敲了一遍）

#include <iostream.h>
#include <string.h>
#define NUM 10
typedef int KeyType;
class AVLTree;
class AVLNode
{
public:
	KeyType key;
	//任意一结点的左子树深度减去右子树的
	//深度称为该节点的平衡因子.
	int bf;      //记录平衡因子
	AVLNode *lchild;
	AVLNode *rchild;
	AVLNode()
	{
		lchild = NULL;
		rchild = NULL;
		bf = 0;
	}
};

//平衡二叉排序树
class AVLTree
{
public:
	AVLNode *root;
	AVLTree()
	{
		root = NULL;
	}
	AVLNode* LL_Rotate( AVLNode *a );     //LL(顺时针)型调整
	AVLNode* RR_Rotate( AVLNode *a );     //RR(逆时针)型调整
	AVLNode* LR_Rotate( AVLNode *a );     //LR(先逆后顺)型调整
	AVLNode* RL_Rotate( AVLNode *a );     //RL(先顺后逆)型调整
	void AVLInsert( AVLNode *&pavlt, AVLNode *s );   //插入一个新结点
}; 

/**
  *  LL(顺时针)型调整
  *  
  */
AVLNode* AVLTree::LL_Rotate( AVLNode *a )
{  
	if( a == NULL )
	{
		cout <<  "the pointer is null!" << endl;
		return NULL;
	}
	AVLNode *b;
	b = a->lchild;       //b指向a的左子树根结点
	a->lchild = b->rchild;  //b的右子树挂在a的左子树上
	b->rchild = a;
	a->bf = b->bf = 0;
	return b;
}

/**
  *  RR(逆时针)型调整
  *  
  */
AVLNode* AVLTree::RR_Rotate( AVLNode *a )
{  
	if( a == NULL )
	{
		cout <<  "the pointer is null!" << endl;
		return NULL;
	}
	AVLNode *b;
	b = a->rchild;
	a->rchild = b->lchild;
	b->lchild = a;
	a->bf = b->bf = 0;
	return b;
}

/**
  *  LR(先逆后顺)型调整
  *  
  */
AVLNode* AVLTree::LR_Rotate( AVLNode *a )
{  
	if( a == NULL )
	{
		cout <<  "the pointer is null!" << endl;
		return NULL;
	}
	AVLNode *b, *c;
	b = a->lchild;
	c = b->rchild;
	a->lchild = c->rchild;
	b->rchild = c->lchild;
	c->lchild = b;
	c->rchild = a;

	//调整平衡因子
	if( c->bf == 1 )
	{
		a->bf = -1;
		b->bf = 0;
	}
	else if( c->bf == -1 )
	{
		a->bf = 0;
		b->bf = 1;
	}
	else
	{
		b->bf = a->bf = 0;
	}
	c->bf = 0;
	return c;
}

/**
  *  RL(先顺后逆)型调整
  *  
  */
AVLNode* AVLTree::RL_Rotate( AVLNode *a )
{  
	if( a == NULL )
	{
		cout <<  "the pointer is null!" << endl;
		return NULL;
	}
	AVLNode *b, *c;
	b = a->rchild;
	c = b->lchild;
	a->rchild = c->lchild;
	b->lchild = c->rchild;
	c->lchild = a;
	c->rchild = b;

	//调整平衡因子
	if( c->bf == 1 )
	{
		a->bf = 0;
		b->bf = -1;
	}
	else if( c->bf == -1 )
	{
		a->bf = 1;
		b->bf = 0;
	}
	else
	{
		a->bf = b->bf = 0;
	}
	c->bf = 0;
	return c;
}

/**
  *  将结点s插入pavlt为根结点的平衡二叉排序树中
  *  
  */
void AVLTree::AVLInsert( AVLNode *&pavlt, AVLNode *s )
{
	AVLNode *f, *a, *b, *p, *q;
	if( pavlt == NULL )
	{
		pavlt = s;
		return;
	}
	a = pavlt;
	f = NULL;
	p = pavlt;
	q = NULL;
	//寻找插入点位置及最小不平衡树的子树
	while( p != NULL )
	{
		if( p->key == s->key )   //AVL中已经存在关键字
			return;
		if( p->bf != 0 )         //寻找最小不平衡子树
		{
			a = p;
			f = q;
		}
		q = p;
		if( s->key < p->key )    
			p = p->lchild;
		else
			p = p->rchild;
	}

	if( s->key < q->key )        //将结点*s插入到合适的位置上去
		q->lchild = s;
	else
		q->rchild = s;
	p = a;
	while( p != s )            //插入结点后修改相应的平衡因子
	{
		if( s->key < p->key )
		{
			p->bf++;
			p = p->lchild;
		}
		else
		{
			p->bf--;
			p = p->rchild;
		}
	}
	if( a->bf > -2 && a->bf < 2 )  //插入结点后没有破坏平衡树
		return;
	if( a->bf == 2 )
	{
		b = a->lchild;
		if( b->bf == 1 )           //结点插在*a的左孩子的左子树中
			p = LL_Rotate( a );    //LL型调整
		else                       //结点插在*a的左孩子的右子树中
			p = LR_Rotate( a );    //LR型调整
	}
	else
	{
		b = a->rchild;
		if( b->bf == 1 )          //结点插在*a的右孩子的左子树中
			p = RL_Rotate( a );   //RL型调整
		else                      //结点插在*a的右孩子的右子树中
			p = RR_Rotate( a );   //RR型调整
	}
	if( f == NULL )               //原*a是AVL树的根
		pavlt = p;
	else if( f->lchild == a )     //将新子树链到原结点*a的双亲结点上
		f->lchild = p;
	else 
		f->rchild = p;
}

/**
  *   在VC6.0下测试成功
  *   cheneagle：2009.8.6 
  */
int main( void )
{
	int a[NUM] = { 34, 18, 13, 73, 16, 52, 58, 67, 82, 76 };
	int i = 0;
	AVLTree tree;
	AVLNode pNode[NUM], *p = NULL;
	for( i = 0; i < NUM; i++ )
	{
		pNode[i].key = a[i];
		tree.AVLInsert( p, &pNode[i] );
	}
	return 0;
}

关于二叉平衡树的删除，我们也是先用二叉搜索树的删除节点方法（较插入复杂），然后再调整。

以后有时间了也写一遍删除的代码。