程序员编程技术学习笔记——最长回文子串
程序员编程技术学习笔记——最长回文子串
1. 题目描述
给定一个字符串,求它的最长回文子串的长度。例如:abaaaabaaa的最长回文子串就是以b为中心,长度为7的回文子串aaabaaa.
2. 解法1:中间扩展法
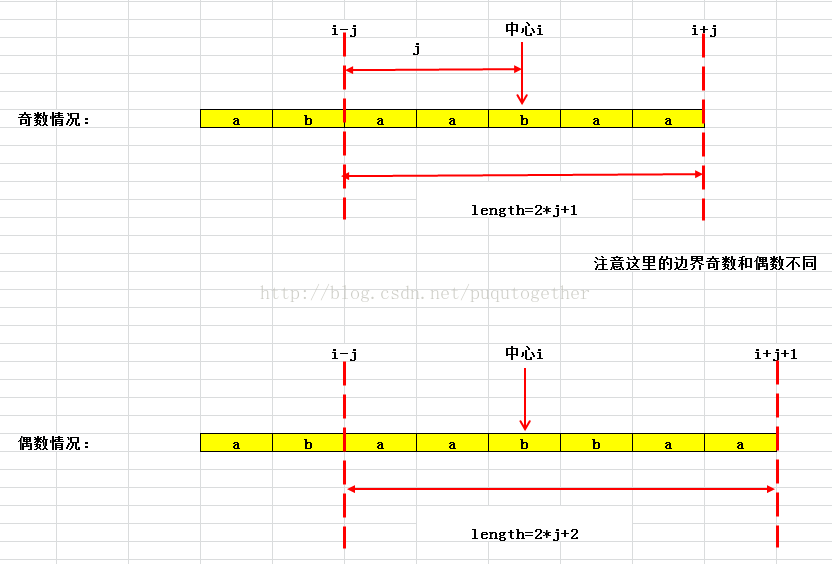
我们可以以字符串中每一个字符为中心,往左右两边扩展,在满足回文字符串条件下,能够扩展的最大长度就是回文子串的长度。注意:这种方法需要考虑子串长度奇数/偶数的不同情况。整个过程如下图:
上述方法需要注意奇数和偶数情况的不同,一个不同在于边界(奇数为i-j和i+j;偶数为i-j和i+j+1);另一个不同是长度(奇数是2*j+1;偶数是2*j+2)。也正是因为这种方法需要分情况讨论,导致有麻烦的缺点。而且,遍历每一个字符为中心的时候,始终都要从j=1开始遍历,时间复杂度也比较大。
这种解法的代码如下:
#include<iostream>
#include<string.h>
using namespace std;
int LongestPalindrome(char *str, int len)
{
int i, j;
int maxlen=0, templen;
for(i=0; i<len; i++) //±éÀúÿ¸ö×Ö·û
{
for(j=0; (i-j)>=0 && (i+j)<=len; j++)
{
if(str[i-j]!=str[i+j])
break;
templen=2*j+1;
}
if(templen>maxlen)
maxlen=templen;
for(j=0; (i-j)>=0 && (i+j+1)<=len; j++)
{
if(str[i-j]!=str[i+j+1])
break;
templen=2*j+2;
}
if(templen>maxlen)
maxlen=templen;
}
return maxlen;
}
int main()
{
char str[10]="abaacaa";
int len=strlen(str);
int maxlen=LongestPalindrome(str, len);
cout<<maxlen<<endl;
return 0;
}
3. 解法2:Manacher算法
Manacher算法是专门用来解决最长回文子串问题的一种算法,其时间复杂度可以达到O(n),其中n是字符串的长度。
从上面解法演变到这个算法的逻辑过程还是这样的:上面算法比较麻烦的是需要讨论奇数偶数的情况,而且每次以第i个字符为中心扩展的时候,都要从长度为1开始扩展,导致了时间复杂度比较大。那么我们能不能让串的长度始终都是奇数呢?(因为奇数的情况更加简单一些)再有,我们能不能让后面几次的扩展可以用到前面扩展的先验信息,从而减少时间复杂度呢?
Manacher算法就是从上面两个方面实现优化的。
优化1:首先通过在每个字符的两边都插入一个特殊的符号,将所有可能的奇数或偶数长度的回文子串都转换成了奇数长度。比如 abba 变成 #a#b#b#a#, aba变成 #a#b#a#。此外,为了进一步减少编码的复杂度,可以在字符串的开始加入另一个特殊字符,这样就不用特殊处理越界问题,比如$#a#b#a#。以字符串12212321为例,插入#和$这两个特殊符号,变成了 S[] = "$#1#2#2#1#2#3#2#1#"。这一步就让串长变成了奇数。
优化2:然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左或向右扩张的长度(包括S[i])。最长回文子串的长度就是P数据中最大值-1. 那么显然,这种算法的关键之处就是如何求得算法P,求数组P的过程就实现了后面的数可以用到前面的数的先验信息,从而减少了时间复杂度。
我们可以通过下图来展示如何求数据P:
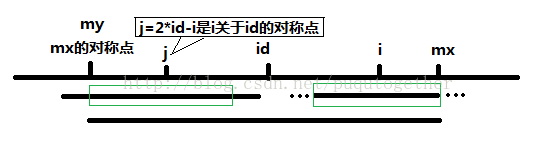
首先我们引入两个辅助变量id和mx,其中id表示最大回文子串中心的位置,mx则为id+P[id],也就是最大回文子串的边界。id和mx初始化都是0。在求第i个字符处可扩展的回文子串时,我们可以针对i和id的相对位置分情况讨论:
1)当i+P[ j ]<mx的时候,以i为中心,P[ j ]为半径扩展的子串就已经在以id为中心mx为范围的子串中了。这时,我们就可以直接用i相对于id对称点j的P[ j ]信息,即P[ i ]=P[ j ]。如下图:
2)当i+P[ j ]>=mx的时候,以i为中心,P[ j ]为半径扩展的子串就跳出以id为中心,mx为范围的子串中了。这时,我们可用的先验信息就是P[ i ]>=mx-i,也就是我们只能确定P[ i ]的最小值。如下图:
然后我们再以i为中心,P[ i ]为半径扩展,如果满足回文条件,P[ i ]继续增加。换句话说,刚才求得的P[ i ] 只是一个初始值,我们需要继续扩展判断。
3)当i>=mx的时候,我们也是只能确定P[ i ]的最小值,但是此时由于i已经跳出了mx的范围,所以我们无法用到前面的先验信息,只能认为P[ i ]的最小值为1,这也是最长回文子串的最小长度。然后我们再进行回文判断。
代码如下:
//输入,并处理得到字符串s
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++)
{
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
while (s[i + p[i]] == s[i - p[i]])
p[i]++;
if (i + p[i] > mx)
{
mx = i + p[i];
id = i;
}
}
//找出p[i]中最大的
至此,Manacher算法介绍完毕。我们回头再来看,其实Manacher算法就是把原来的字符串加入了一些标记符号,使得串长始终都是奇数,然后再以id和mx两个辅助变量,快速地对P[ i ]赋值,从而在计算以i为中心的回文子串的过程中,不必每次都从1开始比较,减少了比较次数,最终使得求解最长回文子串的长度达到线性O(N)的时间复杂度。