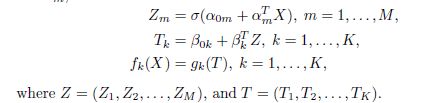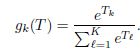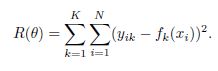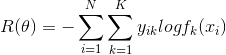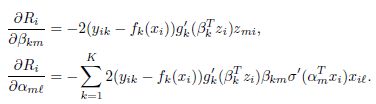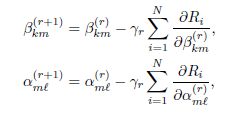BP Neural Networks初步理解

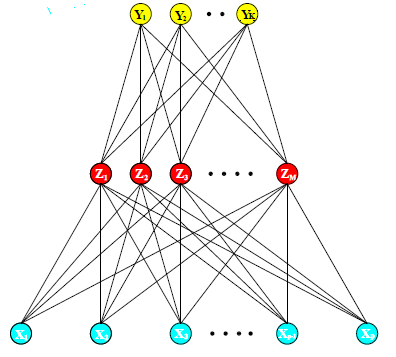
bp神经网络，bp的全称是Back Propagation，中文译为反向传播。首先来一张该神经网络的图：

这是一张只有一层hidden layer的神经网络，它的大致做法可以用这样的式子表示：

其实X是输入层，Y是输出层，Z是隐藏层，alpha和beta都是待估计的参数，第一行那个字母函数一般选择sigmoid函数，而gk(T)这个函数一般是sotfmax函数如下：

需要注意的一点是，每一层到下一层的计算，除了该层的所有点，还会加一个点，那么假如l层到l+1层，那么参数矩阵的维数为( (l+1)层结点个数*l层节点个数+1 ),这个加的节点可以类似理解为线性回归的常数项1。

下面说下神经网络是如何进行拟合参数的，一般来讲，对于回归，有误差函数：

而对于分类，有误差函数：

注意这里的y不是一列向量，而是一个矩阵，如果第i个样本是第k类，那么yik为，否则为0。fk(xi)表示第i个样本是第j类的概率，这个概率用softmax函数可以快速得到。

对于分类的问题，之前做过coursera上面机器机器学习公开课的实验，Andrew Ng采用的最后一层依然是sigmoid函数法，每一层的一个点都是前一层所有点的线性组合然后利用sigmoid函数映射到[0,1]之前的数，最后的结果则是一列向量，每个维度都取(0,1)直接的一个值。可以发现，softmax函数和它的区别只是把最后一层归一化了，其实在分类上，他们的结果应该一致的，因为都是取值最大的那个类作为结果。

其中N为样本个数，以回归为例，每一个Ri对alpha和beta分别求导，得到：

我们的目标是找到最适合的alpha和beta，使得误差最小，那么自然而然想到了梯度下降法，从而有参数的迭代方程：

这个方程组出现了一个学习速率,来代表每次参数改变的多少。

在具体实现过程中，先随机取参数，然后正向计算出各个隐藏层的值，最后算得最后的估计值，而这个估计值存在误差，需要修改各层之间的参数，每一次参数的变化都是按照使得误差变小的方向前进一段距离，这个参数修改的过程是逆着的，就是离输出层最近的参数先被修改，这也就是所谓的反向传播,每次修改好参数，再通过修改后的参数计算输出层，在计算误差，误差过大再修改参数，一直到误差小到一定程度为止。

神经网络参数的初始值一般取接近0的随机数，另外对于每层节点的个数，the elements大概也有说明，每层点的个数大概是5到100个，最后对于过拟合问题，对于上面只有一个hidden层的情况，可以在误差函数中加入

来作为新的代价函数，使得新的误差函数为R(theta)+lambda*J(theta)来解决。