2013南京站I题||hdu4810 二进制枚举

http://acm.hdu.edu.cn/showproblem.php?pid=4810

Problem Description

Ms.Fang loves painting very much. She paints GFW(Great Funny Wall) every day. Every day before painting, she produces a wonderful color of pigments by mixing water and some bags of pigments. On the K-th day, she will select K specific bags of pigments and mix them to get a color of pigments which she will use that day. When she mixes a bag of pigments with color A and a bag of pigments with color B, she will get pigments with color A xor B.
When she mixes two bags of pigments with the same color, she will get color zero for some strange reasons. Now, her husband Mr.Fang has no idea about which K bags of pigments Ms.Fang will select on the K-th day. He wonders the sum of the colors Ms.Fang will get with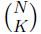  different plans.

For example, assume n = 3, K = 2 and three bags of pigments with color 2, 1, 2. She can get color 3, 3, 0 with 3 different plans. In this instance, the answer Mr.Fang wants to get on the second day is 3 + 3 + 0 = 6.
Mr.Fang is so busy that he doesn’t want to spend too much time on it. Can you help him?
You should tell Mr.Fang the answer from the first day to the n-th day.

 

Input

There are several test cases, please process till EOF.
For each test case, the first line contains a single integer N(1 <= N <= 10 ³).The second line contains N integers. The i-th integer represents the color of the pigments in the i-th bag.

 

Output

For each test case, output N integers in a line representing the answers(mod 10 ⁶ +3) from the first day to the n-th day.

 

Sample Input

   
   
   
   

    
    
    
    4
1 2 10 1
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    14 36 30 8
   
   
   
   

解题思路：

                 一开始拿到这个题感觉有点摸不着头脑，最笨的方法是枚举出所有的种类一个一个的进行异或，但是马上就想到这个方法根本就行不通，先不说超时的问题，就是组合数在longlong范围内就根本不可能取得到。    

                似乎这个题没有什么解法了，但是仔细想想，根异或的特性，对于每一个二进制位我们只有当1的个数为奇数的时候才可能通过异或在该位得到1。因此，我们可以枚举所有二进制位，计算出每个二进制位上1的个数k，我们枚举1~k之间所有的奇数（1,3,5，7……），利用组合数求出各种取法的和然后乘上权值1<<i。

               想到这里，紧接着又出现了一个新的问题，就是求得的和是否等于所求呢？只是枚举的单个位数，我们在取得时候可是要整取的啊？可以这样想，在整取的过程中，把所有的情况全枚举出来之后做异或时还是要各个位单独异或，相互之间没有影响，最后在做完还是要加起来。传统的过程与我们的做法唯一不同的是：他是把一个数的各个二进制位计算出后相加从而得到一个新的数，然后和其他情况计算出的数进行相加取和。而我们是把所有情况中相同的二进制位先相加，然后在对所有的二进制位进行求和。过程不一样，其结果是一致的。问题分析到这里基本上就可以收尾了，下面就是代码实现了

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
const int MOD=1000003;
const int N=1005;

int n,c[N][N],a[N];
int ans[N];

void init()//预处理，先求出组合数
{
    memset(c,0,sizeof(c));
    for(int i=0;i<N;i++)
    {
        c[i][0]=1;
        for(int j=1;j<=i;j++)
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%MOD;
    }
    /*for(int i=0;i<=10;i++)
    {
        for(int j=0;j<=i;j++)
            printf("%d ",c[i][j]);
        printf("\n");
    }*/
}

void get(int n)//统计各个二进制位上有多少个1
{
    for(int i=0;i<32;i++)
    {
        if(n&(1<<i))
            a[i]++;
    }
}
int main()
{
    init();
    while(~scanf("%d",&n))
    {
        int temp;
        memset(a,0,sizeof(a));
        for(int i=0;i<n;i++)
        {
            scanf("%d",&temp);
            get(temp);
        }
        memset(ans,0,sizeof(ans));
        for(int i=1;i<=n;i++)//1~n的所有情况
            for(int j=0;j<32;j++)//所有的二进制位。题目给出数最大不过1000000+3,32位足矣
                for(int k=1;k<=a[j]&&k<=i;k+=2)//从1~a[j]枚举出所有的奇数情况，并且还要保证不能超过i
                    ans[i]=(ans[i]+(LL)c[a[j]][k]*c[n-a[j]][i-k]%MOD*(1<<j%MOD)%MOD)%MOD;//这里的中间过程会爆掉int，需要强制转换一下子
        for(int i=1;i<=n;i++)
            printf(i==n?"%d\n":"%d ",ans[i]);
    }
    return 0;
}