Least Angel Regression

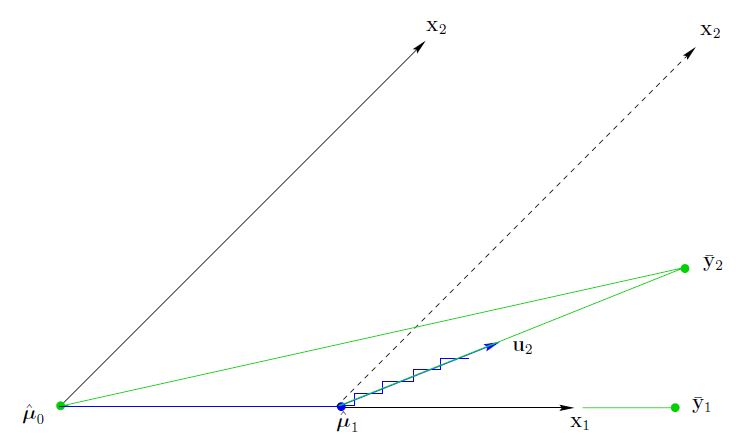
最小角回归和上一篇说的forward stepwise有一些相似的地方是都是将一些variable选到variable集合中来，不一样的是，forward stepwise 每次选的都是与当前残差相关度最大的variable，选进来以后，会重新对所有的入选variable做一下回归，而最小角回归的做法是，同样是首先找到与当前残差相关度最大的variable，然后沿着这个这个variable的方向行径，行经过程中残差与这个variable的相关度会逐渐减小，直到发现了有另外一个variable，它与当前残差的相关度和刚才那个variable与残差的相关度一样了，此时就不往第一个variable的方向行径，而是往这2个variable的方向，那这个方向是什么呢？几何上就是这两个variable方向的角平分线方向，看下下面的图：

这张图说明了这个过程的前两步(记得做之前将x标准化，将y中心化)，首先发现x1比x2更加得和y2相关，所以先沿着x1的方向移动，直到走到u1时，发现x1，x2与此时的残差相关程度一样了，那么此时移动的方向就是x1，x2所呈角的角平分线方向，按照这个方向移动，直到下一个variable出现，按照此过程一直移动，直到所有的variable都被找出来。

方向可以用这个式子来定义，有：

这个式子Xak表示当前入选的variable，相当于用当前的variable对残差rk做了一次regression，可以看出这个方向向量一开始只有一个非0的数，随着variable的增加，0的个数逐渐较少。

每一次更新估计的参数为，

alpha为这个方向移动的距离，移动到出现一个variable和当前入选variable与残差相关度相等时(因为每次都是按照角平分线，所以当前入选的所有variable与残差相关度都是相等的)，移动停止。

值得说明的两点：

1 其实stagewise 从u0走到u1走了走了很多步，因为它选了x1后还是发现x1与当前残差相关性最大，所以他需要非常多的步骤找到u1,更多的步骤找到所有的variable，这个方法过于保守。

2 而对于stepwise,它一下子就找到y1(y1是y2在x1上的投影),也就是y2关于x1做regression的结果，所以说这个方法过于激进。

而Least Angel Regression 则是上面两个方法的折中法。

可以发现，按照这样的path移动，所有被找到的variable和当前残差的相关性都是一样的。如下图：

这图(横坐标是路径的长度)说明了相关性(注意这里都取了绝对值)逐渐下降并且所有被选进的variable相关性相等。

然而最令我费解的是，Least Angel Regression 和Lasso还有一定的关系，如下图：

lasso就是把岭回归参数向量的长度平方改成了绝对值的和，对于这两个方法，有一个重要的性质是：

如果不存在某个参数随着path长度增加而穿过了0这个坐标，那么lasso的解和Least Angel Regression的解是一样的，可以发现图中，在横坐标18以前，图都是一样的，而在18这个位置，深蓝色的线穿过了0。

表示自己水平不够看不懂The elements of statistical learing 里面的解释，就先放在这里吧。