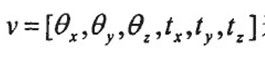关于三维扫描及重建工作
最近一直在做三维扫描及重建的工作,初次涉及,感觉有点麻烦。每次写算法的时候总会产生头痛的感觉,也许是还不适应做算法吧,当然有了经历就好,以后再做到这样的工作应该就会比较上手了。
现在在开发的过程中,我先做一个中途的总结,不然时间一长很多又忘了,到后来东西多了也不想总结了。呵呵,废话就不说了,进入正题吧。
一、三维重建(3D Reconstruction)概述
三维重建是指对三维物体建立适合计算机表示和处理的数学模型,是在计算机环境下对其进行处理、操作和分析其性质的基础,也是在计算机中建立表达客观世界的虚拟现实的关键技术。在计算机视觉中就是将得到的深度数据进行多视角配准、融合和网格化后恢复原本的空间信息,在计算机里建立起三维模型。
通常获取深度数据的方式有:单目(利用到结构光学)、双目(类似于人眼)和激光扫描仪。这里我主要讲的是利用Kinect的红外扫描获取深度数据来进行三维重建,其实网上也有很多人做过(当然更不用说微软公司的KinectFusion计划了),看过他们的视频,效果蛮好的。
二、三维重建中所使用的一些算法
(1)遗传算法
遗传算法来源于生物学,这里我就不讲生物学上的遗传了,我先推荐一本书给大家《遗传算法原理及应用》这里下载:http://wenku.baidu.com/view/9a1cdc7d5acfa1c7aa00cc50.html
遗传算法的工作过程本质上就是模拟生物的进化过程。首先,要规定一种编码方法,使得你的问题的任何一个潜在可行解都能表示成为一个“数字”染色体。然后,创建一个由随机的染色体组成的初始群体(每个染色体代表了一个不同的候选解),并在一段时期中,以培育适应性最强的个体的办法,让它们进化(其实就是交叉),在此期间,染色体的某些位置上要加入少量的变异。经过许多世代后,运气好一点,遗传算法将会收敛到一个解。遗传算法不保证一定能得到解,如果有解也不保证找到的是最优解,但只要采用的方法正确,你通常都能为遗传算法编出一个能够很好运行的程序。
遗传算法的最大优点就是,你不需要知道怎么去解决一个问题;你需要知道的仅仅是,用怎么的方式对可行解进行编码,使得它能能被遗传算法机制所利用。
遗传算法基本流程:
编码方法:
![]() 二进制编码
二进制编码![]() 大字符集编码
大字符集编码![]() 序列编码
序列编码![]() 实数编码
实数编码![]() 树编码
树编码![]() 自适应编码
自适应编码![]() 乱序编码
乱序编码![]() 二倍体和显性规律
二倍体和显性规律
这些编码方式我就不一一讲解了,那本书上基本都有说到,网上可搜。
群体初始化:
自己设定一个染色体群体的大小,随机产生染色体中的DNA。
适应度计算:
适应度的计算是通过适应度约束函数计算的,通过交叉和变异产生的新个体要利用适应度约束函数计算其适应度,再根据选择方法选择出适应性强(适应度大或者小,具体问题具体分析)的染色体。
交叉和变异:
交叉即是将两个染色体的某些DNA按照一定方法互换形成新个体,变异就是将某个染色体的部分DNA进行变化形成新个体。
利用遗传算法粗略求解深度图像配准的R和T
先给个表达式:
等号两边的坐标分别为两幅深度图像的坐标,R和T就是选择矩阵和平移向量,我们的多视点深度图像配准就是求解出R和T。
其中R可以表示为(有的我懒得打公式,就直接将我的文章里的图截取过来,见谅):
//基因组
struct Sgenome
{
vector <float> vecFloatChrom; //浮点数编码染色体
float dFitness; //染色体适应度
void InitSgenome()
{
int i;
for(i = 0;i < 6;i++)
{
if(i < 3)
vecFloatChrom.push_back((rand()*1.0/RAND_MAX)*MAXROTATION);
else
{
switch(i)
{
case 3 : vecFloatChrom.push_back((rand()*1.0/RAND_MAX)*DEPTHX/2);
break;
case 4: vecFloatChrom.push_back((rand()*1.0/RAND_MAX)*DEPTHY/2);
break;
case 5: vecFloatChrom.push_back((rand()*1.0/RAND_MAX)*DEPTHZ/2);
break;
}
}
}
}
};
(2)ICP算法
这里我就不想再多说理论的东西了,网上到处都是,只讲一下算法流程。
![]() 首先利用上面的遗传算法求出的R和T将点集P进行转换,转换后的点集记做Q,然后在另一幅深度图M中寻找P中每个点的最近点,方法就是将每个点看成一个向量,做Q点与M点的差,得到向量V,然后求V的1范数的平方(其实是相当于求两点距离),记为
首先利用上面的遗传算法求出的R和T将点集P进行转换,转换后的点集记做Q,然后在另一幅深度图M中寻找P中每个点的最近点,方法就是将每个点看成一个向量,做Q点与M点的差,得到向量V,然后求V的1范数的平方(其实是相当于求两点距离),记为
![]() 升序排列
升序排列 ,选择N(表示两幅图重叠的点数)个最小值,并计算它们的和ST;
,选择N(表示两幅图重叠的点数)个最小值,并计算它们的和ST;
![]() 当任何终止条件满足时退出,否则执行ST1 = ST;
当任何终止条件满足时退出,否则执行ST1 = ST;
![]() 计算N个选定点的最优R和T(这里的计算使用了四元组法),使ST最小;
计算N个选定点的最优R和T(这里的计算使用了四元组法),使ST最小;
![]() 根据计算的R和T又将P点集进行变换,循环到第一步,当循环达到一定次数或者终止条件满足时退出,得到一个最优的R和T
根据计算的R和T又将P点集进行变换,循环到第一步,当循环达到一定次数或者终止条件满足时退出,得到一个最优的R和T
终止条件: