Codeforces Round #286 (Div. 2) D. Mr. Kitayuta's Technology 强连通分量 有向图求环
Shuseki Kingdom is the world's leading nation for innovation and technology. There are n cities in the kingdom, numbered from 1 to n.
Thanks to Mr. Kitayuta's research, it has finally become possible to construct teleportation pipes between two cities. A teleportation pipe will connect two cities unidirectionally, that is, a teleportation pipe from city x to city y cannot be used to travel from city y to city x. The transportation within each city is extremely developed, therefore if a pipe from city x to city y and a pipe from city y to city z are both constructed, people will be able to travel from city x to city z instantly.
Mr. Kitayuta is also involved in national politics. He considers that the transportation between the m pairs of city (ai, bi) (1 ≤ i ≤ m) is important. He is planning to construct teleportation pipes so that for each important pair (ai, bi), it will be possible to travel from city ai to city bi by using one or more teleportation pipes (but not necessarily from city bi to city ai). Find the minimum number of teleportation pipes that need to be constructed. So far, no teleportation pipe has been constructed, and there is no other effective transportation between cities.
The first line contains two space-separated integers n and m (2 ≤ n ≤ 105, 1 ≤ m ≤ 105), denoting the number of the cities in Shuseki Kingdom and the number of the important pairs, respectively.
The following m lines describe the important pairs. The i-th of them (1 ≤ i ≤ m) contains two space-separated integers ai and bi(1 ≤ ai, bi ≤ n, ai ≠ bi), denoting that it must be possible to travel from city ai to city bi by using one or more teleportation pipes (but not necessarily from city bi to city ai). It is guaranteed that all pairs (ai, bi) are distinct.
Print the minimum required number of teleportation pipes to fulfill Mr. Kitayuta's purpose.
4 5 1 2 1 3 1 4 2 3 2 4
3
4 6 1 2 1 4 2 3 2 4 3 2 3 4
4
For the first sample, one of the optimal ways to construct pipes is shown in the image below:
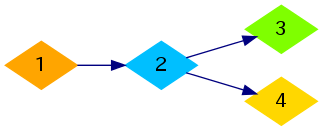
For the second sample, one of the optimal ways is shown below:
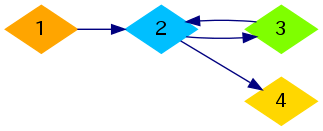
首先,按无向的图来看,分割成连通块,连通块之间,是没有关系的。对于某个连通块,如果,有向连通图没有环,用拓扑排序,就可以排出满足的所有要求,只要用n-1个边(拓扑排序的过程,就满足了所有的要求),如果是有环的连通图,只需要用n个点就可 以了(n个点首尾相连,就可以满足所有的要求)。如何判定有向连通图是否有环呢,只需要,某个点其对应的强连通分量大于2,就说明有环。总的复杂度为求强连通分量o(n + m );
有向图求环,有两种方法
1.拓扑排序,能拓扑排序,自然没环
2.强连通分量,如果大于2结点数,有环,复杂度为o(n + m );适合于本题
#define N 100005
#define M 200005
#define maxn 205
#define MOD 1000000000000000007
//强连通模版
struct Graph{
//N为结点数 Stap 栈 Stop栈最大值 Dclock 时针号 Belong属于哪个Bcnt连通分量的个数
int DFN[N],LOW[N],Stap[N],Stop,Dclock,Belong[N],Bcnt,n;
//是否在栈中
bool instack[N];
vector<pii> p[N];
void tarjan(int i)
{
int j;
DFN[i]=LOW[i]=++Dclock;
instack[i]=true;
Stap[++Stop]=i;
for(int k = 0;k < p[i].size();k++)
{
j = p[i][k].first;
if (!DFN[j])
{
tarjan(j);
if (LOW[j]<LOW[i])
LOW[i]=LOW[j];
}
else if (instack[j] && DFN[j]<LOW[i])
LOW[i]=DFN[j];
}
if (DFN[i]==LOW[i])
{
Bcnt++;
do
{
j=Stap[Stop--];
instack[j]=false;
Belong[j]=Bcnt;
}
while (j!=i);
}
}
//求强连通
void StrongConnected()
{
int i;
Stop=Bcnt=Dclock=0;
memset(DFN,0,sizeof(DFN));
memset(LOW,0,sizeof(LOW));
memset(instack,false,sizeof(instack));
for (i=1;i<=n;i++)
if (!DFN[i])
tarjan(i);
}
//从1开始计数
void init(int nn){
n = nn;
FI(n + 1)
p[i].clear();
}
void AddEdge(int a,int b,int c){
p[a].push_back(mp(b,c));
}
//扩展功能 统计每个强连通分量的个数
int CNum[N];
void GetCount(){
memset(CNum,0,sizeof(CNum));
for (int i=1;i<=n;i++)
CNum[Belong[i]]++;
}
}G1,G2;
//本题要用的
int n,m,a,b,ans,flag;
bool Vis[N];
void DFS(int x){
Vis[x] = true;
if(G1.CNum[G1.Belong[x]] >= 2){
flag++;
}
ans++;
FI(G2.p[x].size()){
int goal = G2.p[x][i].first;
if(!Vis[goal])
DFS(goal);
}
}
int main()
{
//freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
while(S2(n,m)!=EOF)
{
G1.init(n);
G2.init(n);
FI(m){
S2(a,b);
G1.AddEdge(a,b,0);
G2.AddEdge(a,b,0);
G2.AddEdge(b,a,0);
}
G1.StrongConnected();
G1.GetCount();
/*
for(int i = 1;i<=n;i++){
printf(" %d ",G1.Belong[i]);
}
cout<<endl;
*/
ans = 0;
fill(Vis,false);
for (int i=1;i<=n;i++){
if(!Vis[i]){
flag = 0;
DFS(i);
if(!flag)
ans--;
//printf("%d %d\n",flag,ans);
}
}
printf("%d\n",ans);
}
//fclose(stdin);
//fclose(stdout);
return 0;
}
强连通分量的模板
//强连通模版
struct Graph{
//N为结点数 Stap 栈 Stop栈最大值 Dclock 时针号 Belong属于哪个Bcnt连通分量的个数
int DFN[N],LOW[N],Stap[N],Stop,Dclock,Belong[N],Bcnt,n;
//是否在栈中
bool instack[N];
vector<pii> p[N];
void tarjan(int i)
{
int j;
DFN[i]=LOW[i]=++Dclock;
instack[i]=true;
Stap[++Stop]=i;
for(int k = 0;k < p[i].size();k++)
{
j = p[i][k].first;
if (!DFN[j])
{
tarjan(j);
if (LOW[j]<LOW[i])
LOW[i]=LOW[j];
}
else if (instack[j] && DFN[j]<LOW[i])
LOW[i]=DFN[j];
}
if (DFN[i]==LOW[i])
{
Bcnt++;
do
{
j=Stap[Stop--];
instack[j]=false;
Belong[j]=Bcnt;
}
while (j!=i);
}
}
//求强连通
void StrongConnected()
{
int i;
Stop=Bcnt=Dclock=0;
memset(DFN,0,sizeof(DFN));
memset(LOW,0,sizeof(LOW));
memset(instack,false,sizeof(instack));
for (i=1;i<=n;i++)
if (!DFN[i])
tarjan(i);
}
//从1开始计数
void init(int nn){
n = nn;
FI(n + 1)
p[i].clear();
}
void AddEdge(int a,int b,int c){
p[a].push_back(mp(b,c));
}
//扩展功能 统计每个强连通分量的个数
int CNum[N];
void GetCount(){
memset(CNum,0,sizeof(CNum));
for (int i=1;i<=n;i++)
CNum[Belong[i]]++;
}
}G1,G2;