编辑本段概述
最大团问题(Maximum Clique Problem, MCP)是图论中一个经典的组合优化问题,也是一类NP完全问题,在国际上已有广泛的研究,而国内对MCP问题的研究则还处于起步阶段,因此,研究最大团问题具有较高的理论价值和现实意义。
最大团问题又称为最大 独立集问题(Maximum Independent Set Problem)。目前,求解MCP问题的 算法主要分为两类:确定性算法和 启发式算法。确定性算法有回溯法、 分支限界法等, 启发式算法 蚁群算法、顺序贪婪算法、DLS-MC算法和智能搜索算法等。
编辑本段问题描述
给定无向图
G=(
V,
E),其中
V是非空集合,称为顶点集;
E是
V中元素构成的无序二元组的集合,称为边集,无向图中的边均是顶点的无序对,无序对常用圆括号“( )”表示。如果
U∈
V,且对任意两个顶点
u,
v∈
U有(
u,
v)∈
E,则称
U是
G的完全子图。
G的完全子图
U是
G的团当且仅当
U不包含在
G的更大的完全子图中。
G的最大团是指
G中所含顶点数最多的团。
如果
U∈V且对任意
u,
v∈
U有(
u,
v)不属于E,则称
U是
G的空子图。
G的空子图
U是
G的 独立集当且仅当
U不包含在
G的更大的空子图中。
G的最大 独立集是
G中所含顶点数最多的独立集。
对于任一无向图
G=(
V,
E),其补图
G'=(
V',
E')定义为:
V'=
V,且(
u,
v)∈
E' 当且仅当(
u,
v)∉
E。
如果
U是
G的完全子图,则它也是
G'的空子图,反之亦然。因此,
G的团与
G'的 独立集之间存在一一对应的关系。特殊地,
U是
G的最大团当且仅当
U是
G'的最大 独立集
。
编辑本段应用背景
MCP问题是现实世界中一类真实问题,在市场分析、方案选择、信号传输、计算机视觉、故障诊断等领域具有非常广泛的应用。自1957年Hararv和Ross首次提出求解最大团问题的确定性算法以来,研究者们已提出了多种确定性算法来求解最大团问题。但随着问题规模的增大(顶点增多和边密度变大),求解问题的时间复杂度越来越高,确定性算法显得无能为力,不能有效解决这些NP完全问题。
20世纪80年代末,研究者们开始尝试采用 启发式算法求解最大团问题,提出了各种各样的启发式算法,如顺序贪婪启发式算法、 遗传算法、 模拟退火算法、禁忌搜索算法、 神经网络算法等,并且取得了令人满意的效果。在时间上,由于采用了启发式信息, 启发式算法的运算时间与确定性算法的运算时间之间的比值会随着图的顶点、边密度的增加而变得越来越小。唯一的缺点就是不一定能找到 最优值,有时只能找到近优值。
近年来研究表明,单独使用一种 启发式算法求解最大团问题,算法性能往往并不是很好,因此,常借鉴算法之间优势互补策略,形成新的混合启发式算法来求解最大团问题。当前求解该问题最好的 启发式算法有反作用 禁忌搜索(Reactive Tabu Search, RTS)算法、基于 遗传算法的简单启发式算法(Simple Heuristic Based Genetic Algorithm, HGA)、DLS-MC算法等。
编辑本段常用算法
顺序贪婪启发式算法
顺序贪婪启发式算法是最早的求解最大团的启发式算法。这类算法通过给一个团重复进行加点操作得到一个极大团或者对一组并不是团的子图重复进行删除顶点操作以得到一个团。1987年,Kopf和Ruhe把这类型算法分为Best in和Worst out两类。
(1)Best in方法的基本思路:由一个团出发,和这个团中顶点相连的顶点组成候选集;然后以一定的启发式信息,从中选择顶点加入团中,以后反复进行,直到最后得到一个极大团。
(2)Worst out方法的基本思路:从整个顶点集开始,然后按一定的启发式信息,从中反复进行删除顶点操作,直到最后得到一个团。
顺序贪婪 启发式算法有很大不足,该算法一旦找见一个极大团,搜索就停止,因此找到最大团的概率相对较低。
局部搜索启发式算法
假设
SG为图的所有极大团的集合,由于顺序贪婪启发式算法仅能找见
SG中的一个极大团,因此,为了提高解的质量,应当扩大在
SG的搜索区域,比如,可以在极大团
S的邻居中继续进行搜索,以扩大搜索区域,进而提高解的质量。
在局部搜索 启发式算法中,如果搜索
S的邻居越多,提高解的质量的机会就越大。依赖不同的邻居定义,局部搜索 启发式算法可以得到不同的解。在局部搜索 启发式算法中,比较有名的算法是
K-interchange启发式算法,它是一种基于
K-neighbor邻居实现的,在解集
S的
K邻居中进行局部搜索的方法。
分析可知,局部搜索 启发式算法存在一个问题,即仅能够找见一个局部 最优值。所以为了提高求解的质量,常把该算法和其它算法相混合,从而得到求解MCP问题的新的算法。
WaynePullan和HolgerH.Hoos基于这一思想提出了求解最大团问题的DLS-MC 算法,该算法是plateau search局部搜索启发式和算法迭代改善法相混合得到的,算法性能非常好,在该方法中引入了顶点 惩罚函数,该函数在算法的求解过程中能够动态改变;在算法执行过程中迭代改善法和plateau search算法轮流执行来提高解的质量。在基准图上对该 算法进行了测试,性能非常好。
智能搜索启发式算法
智能搜索算法主要有遗传算法、禁忌算法、模拟退火算法、神经网络等。
遗传算法
遗传算法(Genetic Algorithm, GA)是一种基于自然选择和群体遗传机理的搜索算法,它模拟了自然选择和自然遗传过程中发生的复制、交叉和变异现象。
1993年,Carter和Park首次提出使用 遗传算法求解最大团问题,但由于所求解的质量差,计算 复杂度高,因此,他们认为遗传算法并不适合求解最大团问题。与此同时,Bäck和Khuri致力于最大独立集问题的求解,却得到了完全相反的结论,通过选用合适的适应度函数,取得了很好的效果。因此在使用GA来解决最大团问题时, 适应度函数起着非常关键的作用。此后,基于 遗传算法求解最大团问题的方法逐渐增多,但在提高解的质量,降低算法复杂度上方面却没有大幅度的提高。
l998年,Marchiori提出了一种基于 遗传算法的简单 启发式算法(simple heuristic based genetic algorithm, HGA)。 算法由两部分组成:简单 遗传算法(simple genetic algorithm, SGA)和简单的贪婪启发式局部搜索算法(simple greedy heuristic local search algorithm,SGHLSA)。在基准图上对算法HGA的性能进行测试,证明了该算法在解的质量和计算速度方面都优于基于 遗传算法的其它算法。
因此,单纯使用 遗传算法(改动变异、 杂交、选择等算子)求解最大团问题时,算法的性能是比较差;要提高算法性能,遗传算法最好能和局部搜索算法相结合。
模拟退火算法
模拟退火(Simulated Annealing, SA)算法是N. Metropolis在1953年提出的一种基于物质退火过程的随机搜索算法,是一种迭代求解的启发式随机搜索算法。首先在 高温下较快地进行搜索,使系统进入“ 热平衡”状态,大致地找到系统的低能区域。随着温度的逐渐降低,搜索精度不断提高,可逐渐准确地找到最低 能量的 基态。作为局部搜索算法的扩展,当邻域的一次操作使当前解的质量提高时,接受这个改进解作为新的当前解;反之,以一定的概率接受相对质量比较差的解作为新的当前解。
Aarts和Korst提出使用 模拟退火算法来解决 独立集问题,建议在算法设计时引入 惩罚函数,但却没有提供任何的实验结果。问题的解空间
S是图
G的全部可能的子图,并不要求是 独立集,对于任一子图
G*,成本函数为
f(
V')=|
V'|- k|
E'|,其中
V'是图
G*的顶点集,
E'是图
G*的边集,k是权因子(k>1)。选择邻居时,费用值大的将被选中,因此求解最大 独立集问题也就是最大化成本函数问题。
Homer和Peinado把 模拟退火算法和Johnson的贪婪 启发式算法、Boppan的 随机化算法、Halldorsson的子图排除法3种启发式算法进行比较,结果比这3种算法要好很多。总之, 模拟退火算法在处理最大团问题上是一个非常好的算法。
禁忌算法
禁忌算法(Tabu Algorithm)是一种改进的局部搜索算法。该算法为了避免在搜索过程中出现死循环和开发新的搜索区域,采用了一种基于禁止的策略。
1989年,Friden提出了基于 禁忌搜索的求解最大 独立集的 启发式算法,独立集的大小固定,该算法的目标是最小化当前子集(解)顶点之间的边数。使用3个禁忌表:其中,一个禁忌表用来存放上一代的解,另外两个分别存放刚进入解顶点和刚被删去的顶点。
基于禁忌 算法求解最大团问题具有代表性的是Batti和Protasi提出的反作用局部搜索(Reaction Local Search, RLS)算法,通过引入局部搜索算法,扩展了 禁忌搜索的框架。与一般禁忌搜索算法相比,该算法的特点是:在执行过程中,根据所得到的解的情况形成一种内部 反馈机制以控制调整算法的控制参数,所以该算法的控制参数是动态变化的;比如,禁止表长度参数是动态变化的,因此禁忌表长度是动态变化的。他们在DIMACS的基准图上对 算法性能进行测试,取得非常好的效果。
神经网络算法
人工神经网络指为了模拟生物大脑的结构和功能而构成的一种大型的、分布式系统,它有很强的自组织性、自适应性和学习能力。
20个世纪80年代末期,Ballard、Godbeerl、Ramanujam和Sadayappan等都尝试对最大团和相关问题按 人工神经网络进行编码,进而求解该问题。然而,这些研究只提供了很少的实验结果。
Grossman提出一种离散的/确定性的Hopfield模型来求解最大团。这个模型有一个用来决定网络是否处于稳定态的临界值参数。Grossman建议在这个参数上使用退火策略,并且使用自适应机制选择网络的初始状态和临界值。在DIMACS基准图上测试,得到比较好的结果,但与性能好的 启发式算法相比,其结果较差,比如结果要差于 模拟退火算法。1995年Jagota对Hopfield模型进行了多处修改来近似求解最大团问题,其中有的是 离散化的,有的是连续的;虽然有了一定改进,但是性能并没有显著提高。随后,仍然有好多研究者使用Hopfield神经网络来求解最大团问题,但是与其它智能搜索 算法相比,效果比较差。
研究表明:(1) 前3种智能搜索 算法适合求解MCP,而通过 神经网络算法求解MCP时的性能比较差;(2) 单独使用智能搜索算法来求解MCP,算法性能并不好,因此,常和局部搜索算法相结合形成新的混合算法,比如:禁忌算法与局部搜索算法相混合形成的反作用禁忌搜索算法, 遗传算法与局部搜索算法相混合形成的简单 启发式算法等。
改进蚁群算法-AntMCP
蚁群算法是由Dorigo M.等人依据模仿真实的蚁群行为而提出的一种模拟进化算法。蚂蚁之间是通过一种称为 信息素(Pheromone)的 物质传递信息的,蚂蚁能够在经过的路径上留下该种物质,而且能够感知这种物质的存在及其强度,并以此来指导自己的 运动方向。因此,由大量蚂蚁组成的集体行为便表现出一种信息正反馈现象:某一条路径上走过的蚂蚁越多,该路径上留下的信息素就越多,则后来者选择该路径的 概率就越大。蚂蚁之间就是通过这种信息素的交流,搜索到一条从 蚁巢到食物源的最短路径。
2003年,Fenet和Solnon提出了求解最大团问题的 蚁群算法AntClique,该算法仍然将信息素留在边上,信息素t
ij是指把结点
i和结点
j分配到同一个团中的期望。由于没有使用局部启发信息,这使得迭代初期各候选顶点的选择概率几乎相等,这样算法在迭代初期有一定的盲目性,往往需要更多的迭代次数才能得到 最优解。针对这些不足及最大团问题的特点,曾艳于2010年提出了改进的 蚁群算法-AntMCP。
算法伪代码描述如下:
Procedure Vertex_AntClique
Initialize //初始化信息素和局部启发信息
Repeat
For
k in 1...nbAnts do:
Choose randomly a first vertex
v f∈V
Ck←{
v f }
Candidate ¬{
v i |(
v f,
v i)
∈E}
While Candidate≠0 do
Choose a vertex
v i∈Candidate withprobability
p(
v i);
Ck←
Ck∪{
v i}
Candidate ←Candidate ∩{
v j |(
vi,
v j)
∈E}
End of while
Endof for
Updatepheromone w.r.t {C1,…,CnbAnts}
Until max cyclesreached or optimal solution found
End of procedure
在AntMCP中,增加了局部启发信息;信息素t和启发信息h不是留在边上,而是留在顶点上。这样,变量t和h由二维降为一维,既可节省存储空间,又可提高运行速度,大量实验表明,该算法运算速度更快,效率更高。
其它启发式算法
除上述几种启发式算法外,目前研究者们还提出了一些新的算法。当图的顶点数不大于阈值
M时,称此图为低度图,求解低度图的最大团问题的时间复杂度为
O(
d),基于这一思想,王青松和范铁生提出了一种求解低度图的最大团的确定性算法。在该算法中,通过对图按顶点逐步分解实现分别计算,较好地解决了低度图的最大团问题,算法的时间复杂度为
O(
d*n^3)。针对遗传算法在最大团求解中保持群体多样性能力不足、早熟、耗时长、成功率高等缺陷,依据均匀设计抽样理论对交叉操作进行重新设计,结合免疫机理定义染色体浓度设计克隆选择策略,周本达、岳芹等提出了一种求解最大团问题的均价设计抽样免疫遗传算法。仿真算例表明,该算法在解的质量、收敛速度等各项指标上均有提高,与DLS-MC、QUALEX等经典搜索算法相比,对部分算例能得到更好解。吴冬辉和马良提出了基于遗传算法的最大团问题求解算法,通过引入概率模型指导变异产生新的个体,并结合启发式局部算法搜索最大团。实例结果验证了该算法的有效性。针对求解最大团问题的分层的边权网络(Hierarchical Edge-Weight Network,HEWN)算法,郭长庚和潘晓伟设计了一个实现HEWN算法的数据结构,指出在HEWN算法中HEWN算法的存储宜采用邻接多重表和二叉表相结合的链表表示法,并进行了时间复杂度分析,得出HEWN算法的时间复杂度是指数级而不是
O(
n^8.5)。针对基于适应值的选择交叉机制在优化具有欺骗性的最大团问题中性能退化的问题,张雁、党群等提出了一种新的基于匹配教程的Memetic算法。算法中提出交叉匹配度的概念,用来估计两个体交叉所能获得的最佳适应值。通过匹配度的计算对交叉方向的选择进行控制,保证了交叉操作以较大的概率生成新的优良模式。测试结果表明,该算法优于目前在最大团问题求解中性能最好的多阶段动态局部搜索算法。DNA计算是应用分子生物技术进行计算的新方法,具有高度并行性、大容量、低能耗等特点。针对这一特点,李涛提出了用DNA算法求解最大团问题,开创了以生物技术为工具解决复杂问题的新纪元,为解决NP完全问题开辟了一条新途径。基于对粘贴模型的组成、基本实验及其生化实现过程的分析,根据最大团问题的需求,周康、刘朔等在粘贴模型中,提出了基于电泳技术和分离实验的DNA序列检测方法。基于分离实验提出了一种求解最大团问题的DNA算法,并给出了其生化实现过程。为了提高交叉熵算法求解最大团问题的性能,吕强、柏战华等提出了一种领导者-跟随者协作求解的并行策略来实现交叉熵算法,从而达到减少计算时间和保障解的质量两者的平衡。算法中领导者活跃在并行处理器之间采集数据,并根据当前获得信息对跟随者作出决策;受控的跟随者则主要根据领导者的决策信息自适应地调整搜索空间,完成各自的集团产生任务。实验结果表明该算法较基于种群的启发式算法有一定的性能改善。
回溯法
回溯法(BacktrackingAlgorithm, BA)有“通用的解题法”之称,用它可以系统地搜索一个问题的所有解或任一解,是一个既带有系统性又带有跳跃性的搜索算法。在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,总是先判断该结点是否肯定不包含问题的解,如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按照深度优先的策略进行搜索。BA在用来求问题的所有解时,要回溯到根,且根结点的所有子树都已被搜索遍才结束。而BA在用来求问题的任一解时,只要搜索到问题的一个解即可结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于解一些组合数较大的问题。
回溯法搜索 解空间树时,根节点首先成为一个活结点,同时也成为当前的扩展节点。在当前扩展节点处,搜索向纵深方向移至一个新节点。这个新节点就成为一个新的活结点,并成为当前扩展节点。如果当前扩展节点不能再向纵深方向移动,则当前的扩展节点就成为死结点。此时,往回回溯至最近的一个活节点处,并使这个活结点成为当前的扩展节点。
回溯法以这种方式递归地在 解空间中搜索,直至找到所有要求的解或解空间已无活结点为止。
搜索:回溯法从根结点出发,按深度优先策略遍历解空间树,搜索满足约束条件的解。
剪枝:在搜索至树中任一结点时,先判断该结点对应的部分解是否满足 约束条件,或者是否超出 目标函数的界;也即判断该结点是否包含问题的解,如果肯定不包含,则跳过对以该结点为根的子树的搜索,即剪枝(Pruning);否则,进入以该结点为根的子树,继续按照深度优先的策略搜索。
一般来讲,回溯法求解问题的基本步骤如下:
(1)针对所给问题,定义问题的 解空间;确定易于搜索的解空间结构;以深度优先方式搜索解空间,并在搜索过程中利用Pruning函数剪去无效的搜索。
(2) 无向图
G的最大团问题可以看作是图
G的顶点集
V的子集选取问题。因此可以用子集树表示问题的 解空间。设当前扩展节点
Z位于 解空间树的第
i层。在进入左子树前,必须确认从顶点
i到已入选的顶点集中每一个顶点都 有边相连。在进入右子树之前,必须确认还有足够多的可选择顶点使得 算法有可能在右子树中找到更大的团。
(3)用 邻接矩阵表示图
G,
n为
G的顶点数,
cn存储当前团的顶点数,
bestn存储最大团的顶点数。
cn+n-i为进入右子树的上界 函数,当
cn+n-i<
bestn时,不能在右子树中找到更大的团,利用剪枝函数可将
Z的右结点剪去。
实例分析
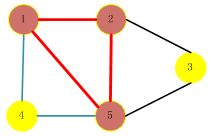
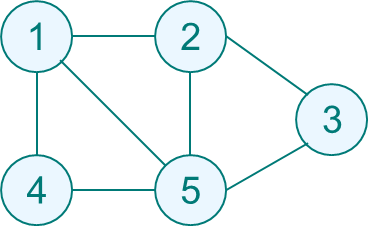
图1
如图1所示,给定无向图
G={
V,
E},其中
V={1,2,3,4,5},
E={(1,2), (1,4), (1,5),(2,3), (2,5), (3,5), (4,5)}。根据MCP定义,子集{1,2}是图
G的一个大小为2的完全子图,但不是一个团,因为它包含于
G的更大的完全子图{1,2,5}之中。{1,2,5}是
G的一个最大团。{1,4,5}和{2,3,5}也是
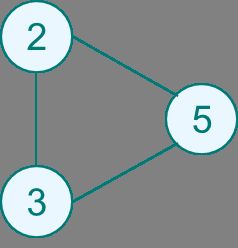
G的最大团。图2是无向图
G的补图
G'。根据最大独立集定义,{2,4}是
G的一个空子图,同时也是
G的一个最大独立集。虽然{1,2}也是
G'的空子图,但它不是
G'的独立集,因为它包含在
G'的空子图{1,2,5}中。{1,2,5}是
G'的最大独立集。{1,4,5}和{2,3,5}也是
G'的最大
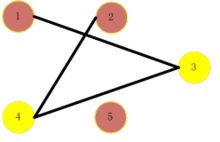
图2
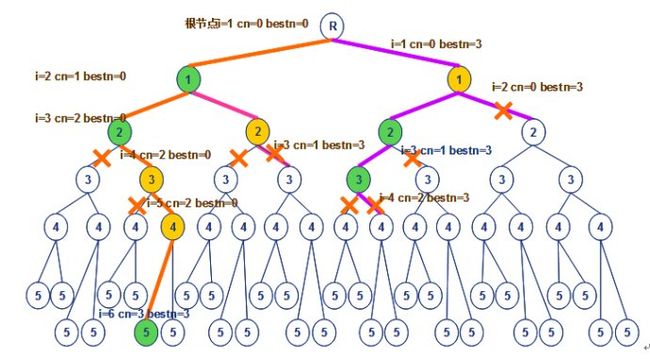
独立集。以图1为例,利用回溯法搜索其空间树,具体搜索过程(见图3所示)如下:假设我们按照1®2®3®4®5的顺序深度搜索。开始时,根结点
R是唯一活结点,也是当前扩展结点,位于第1层,此时当前团的顶点数
cn=0,最大团的顶点数
bestn=0。在这个扩展结点处,我们假定
R和第二层的顶点1之间有边相连,则沿纵深方向移至顶点1处。此时结点
R和顶点1都是活结点,顶点1成为当前的扩展结点。此时当前团的顶点数
cn=1,最大团的顶点数
bestn=0。继续深度搜索至第3层顶点2处,此时顶点1和2有边相连,都是活结点,顶点2成为当前扩展结点。此时当前团的顶点数
cn=2,最大团的顶点数
bestn=0。再深度搜索至第4层顶点3处,由于顶点3和2有边相连但与顶点1无边相连,则利用剪枝函数剪去该枝,此时由于
cn+n-i=2+5-4=3>
bestn=0,则回溯到结点2处进入右子树,开始搜索。此时当前团的顶点数
cn=2,最大团的顶点数
bestn=0。再深度搜索至第5层顶点4处,由于顶点3和4无边相连,剪去该枝,回溯到结点3处进入右子树,此时当前团的顶点数
cn=2,最大团的顶点数
bestn=0。继续深度搜索至第6层顶点5处,由于顶点5和4有边相连,且与顶点1和2都有边相连,则进入左子树搜索。由于结点5是一个叶结点,故我们得到一个可行解,此时当前团的顶点数
cn=3,最大团的顶点数
bestn=3。
vi的取值由顶点1至顶点5所唯一确定,即
v=(1, 2, 5)。此时顶点5已不能再纵深扩展,成为死结点,我们返回到结点4处。由于此时
cn+n-i=3+5-6=2<
bestn=3,不能在右子树中找到更大的团,利用剪枝函数可将结点4的右结点剪去。以此回溯,直至根结点
R再次成为当前的扩展结点,沿着右子树的纵深方向移动,直至遍历整个解空间。最后得到图1的按照1®2®3®4®5的顺序深度搜索的最大团为
U={1,2,5}。当然{1,4,5}和{2,3,5}也是其最大团。
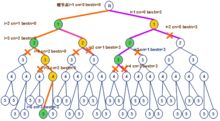
图3
C++ 代码
//MaxClique.cpp : 定义控制台应用程序的入口点。
/*
回溯法求解最大团问题
*/
#include <fstream>
#include <iostream>
#include <stdlib.h>
#include <conio.h>
using namespace std;
#define MAX_v 50 //定义一个最大顶点个数
typedef struct{
int a[MAX_v][MAX_v]; //无向图G的邻接矩阵
int v; //无向图G的顶点
int e; //无向图G的边
int x[50]; //顶点与当前团的连接,x[i]=1 表示有连接
int bestx[50]; //当前最优解
int cnum; //当前团的顶点数目
int bestn; //最大团的顶点数目
}MCP;
void Creat(MCP &G);
void Backtrack(MCP &G,int i);
void Creat(MCP &G){
int i,j;
ifstream fin("data.txt");
if (!fin)
{
cout<<"不能打开文件:"<<"data.txt"<<endl;
exit(1);
}
fin>>G.v;
for (int i=1;i<=G.v;i++)
for (int j=1;j<=G.v;j++)
fin>>G.a[i][j];
for(i=1;i<=G.v;i++) //初始化
{
G.bestx[i]=0;
G.x[i]=0;
G.bestn=0;
G.cnum=0;
}
cout<<"————————————————"<<endl;
cout<<"———回溯法求解最大团问题———"<<endl;
cout<<"————————————————"<<endl;
cout<<"输入初始化无向图矩阵为:"<<endl; //初始化
for(i=1;i<=G.v;i++)
{
for(j=1;j<=G.v;j++)
cout<<G.a[i][j]<<" ";
cout<<endl;
}
}
void Backtrack(MCP &G,int i){
if (i>G.v){
for (int j=1; j<=G.v; j++)
G.bestx[j] = G.x[j];
G.bestn =G.cnum;
return ;
}
//检查顶点i与当前团的连接
int OK = 1;
for (int j=1; j<=i ; j++)
if (G.x[j]&& G.a[i][j]==0){
//i不与j相连
OK = 0;
break;
}
if (OK) {
G.x[i] = 1;//把i加入团
G.cnum++;
Backtrack(G,i+1);
G.x[i]=0;
G.cnum-- ;
}
if (G.cnum+G.v- i>G.bestn){
G.x[i] = 0;
Backtrack(G,i+1);
}
}
int main(){
MCP G;
Creat(G);
Backtrack(G,1);
cout<<"最大团包含的顶点数为:"<<G.bestn<<endl;
cout<<"最大团方案为:( ";
for (int i=1;i<=G.v;i++)
if(G.bestx[i]==1){
cout<<i<<" ";
}
cout<<")"<<endl;
getch();
}
分支限界法
分支限界(Brandand Bound)法类似于回溯法,也是一种在问题的 解空间树上搜索问题的解的算法。
分支限界法常以广度优先或最小耗费(最大效益)优先的方式搜索解空间树。在 分支限界法中,每一个活结点只有一次机会成为扩展结点。一旦活结点成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,舍弃那些导致不可行解或导致非 最优解的儿子结点,将其余儿子结点加入活结点表中。此后,从活结点表中取下一个结点成为当前扩展结点,并重复上述结点扩展过程,直至找到所需的解或活结点表为空时为止。
具体来讲, 分支限界法由“分支”策略和“限界”策略两部分组成。“分支”体现在对问题空间是按广度优先搜索;“限界”策略是为了加速搜索速度而采用启发式剪枝的策略。分支搜索法采用广度优先的策略,依次生成E结点所有分支(即所有的子结点)。在生成的结点中,将采用更有效的约束函数(限界函数)控制搜索路径,去除那些不满足 约束条件(即不可能导出 最优解)的结点,使之能更好地朝着 状态空间树上有最优解的分支推进。
根据从活结点表中选择下一个扩展结点的方式的不同, 分支限界法主要分为以下两类:
1.队列式(FIFO) 分支限界法
队列式 分支限界法将活结点表组织成一个队列,并按队列的FIFO原则选取下一个结点成为当前扩展结点。具体流程为:
A.初始化,根结点是唯一的活结点,根结点入队。
B.从活结点队中取出根结点后,作为当前E结点。对当前E结点,先从左到右地产生它的所有儿子,用约束条件检查,把所有满足约束 函数的儿子加入活结点队列中。
C.重复上述过程:再从活结点表中取出队首结点(队中最先进来的结点)为当前E结点,……;直到找到一个解或活结点队列为空为止。
2.优先队列式 分支限界法
优先队列式 分支限界法将活结点表组织成一个优先队列,并按优先队列中规定的结点优先级选取优先级最高的下一个结点成为当前扩展结点。具体流程为:对每一活结点计算一个优先级,并根据这些优先级,从当前活结点表中优先选择一个优先级最高(最有利)的结点作为扩展结点,使搜索朝着解空间树上有 最优解的分支推进,以便尽快地找出一个最优解。
C++ 代码
//MaxClique_BB.cpp : 定义控制台应用程序的入口点。
/*
分支限界法求解最大团问题
*/
#include <fstream>
#include <iostream>
#include <queue>
#include <conio.h>
using namespace std;
typedef struct{
int v; //无向图G的顶点
int e; //无向图G的边
int a[50][50]; //定义图G的邻接矩阵
int bestx[50]; //最优解
}MCP;
void Creat(MCP &G){
int i,j;
ifstream fin("data.txt");
if(!fin)
{
cout<<"不能打开文件:"<<"data.txt"<<endl;
exit(1);
}
fin>>G.v;
for(int i=1;i<=G.v;i++)
for(int j=1;j<=G.v;j++)
fin>>G.a[i][j];
for(i=1;i<=G.v;i++) //初始化
{
G.bestx[i]=0;
}
cout<<"————————————————————————"<<endl;
cout<<"———优先队列式 分支限界法求解最大团问题———"<<endl;
cout<<"————————————————————————"<<endl;
cout<<"输入初始化无向图矩阵为:"<<endl; //初始化
for(i=1;i<=G.v;i++)
{
for(j=1;j<=G.v;j++)
cout<<G.a[i][j]<<" ";
cout<<endl;
}
}
struct BBNode
{
BBNode *parent; //指向父结点的指针
bool LChild; //左儿子结点标志
};
struct CliqueNode //定义优先队列类型为CliqueNode
{
int cnum; //当前团的顶点数
int un; //当前团最大顶点数的上界
int level; //结点在子集空间树种所处的层次
BBNode *p; //指向活结点在子集树中相应结点的指针
bool operator<(const CliqueNode &b) const //<号重载建立大根堆
{
if (b.un>un) return true;
if (b.un==un&& b.cnum>cnum) return true;
else return false;
}
};
void BBMaxClique(MCP&G)
{
BBNode *E=new(BBNode); //定义B代表记录的队列情况
//初始化
int j,i=1;
int cnum=0,bestn=0;
int OK=1;
priority_queue<CliqueNode> Q; //定义优先队列Q
E->LChild=false; //初始化
E->parent=NULL;
while(i!=G.v+1)//非 叶结点
{
//检查顶点i与当前团中其它顶点之间是否 有边相连
OK=1;
BBNode *B=E; //把当前点的数据给B,B为中间变量
for(j=i-1;j>0;B=B->parent,j--)
if(B->LChild&& G.a[i][j]==0) //如果不满足就停止
{
OK=0;
break;
}
if(OK) //满足条件,即左儿子结点为可行结点
{
CliqueNode *D=new(CliqueNode); //定义一个节点D
D->p=new(BBNode);
if(cnum+1>bestn)bestn=cnum+1;
D->cnum=cnum+1;
D->level=i+1;
D->p->LChild=true;
D->p->parent=E;
D->un=cnum+1+G.v-i;
Q.push(*D); //进队列
}
if(cnum+G.v-i>bestn) //不满足条件但是还是可能有最优解
{
CliqueNode *D=new(CliqueNode); //定义一个节点D
D->p=new(BBNode);
D->cnum=cnum;
D->level=i+1;
D->p->LChild=false;
D->p->parent=E;
D->un=cnum+G.v-i;
Q.push(*D); //进队列
}
CliqueNode N;
N=Q.top(); //取队顶元素,最大堆
Q.pop(); //删除队顶元素
E=N.p; //记录当前团的信息
cnum=N.cnum; //记录当前团的顶点数
i=N.level; //所在的层次
}
for(j=G.v;j>0;j--) //保存最优解
{
G.bestx[j]=E->LChild;
E=E->parent;
bestn=cnum;
}
}
int main(){
MCP G;
Creat(G);
BBMaxClique(G);
cout<<"最大团方案为:(";
for(int i=G.v;i>0;i--)
if (G.bestx[i]==1){
cout<<i<<" ";
}
cout<<")"<<endl;
getch();
}
[1]
poj1129_四色问题
题意:染色问题,图中之间有边的两个区域不能染成相同的颜色。求将图中每个区域全部染色后需要最少的颜色。
分析:参考染色定理得,无论图中有多少区域,最多需要4个区域。因此遍历这四种情况即可.
代码:

 View Code
View Code

1 #include <iostream>
2 #include <stdio.h>
3 #include <memory.h>
4 using namespace std;
5
6 const int maxnum=27;
7 bool array[maxnum][maxnum];
8 int num;
9
10 void fuction()
11 {
12 int i,j,k,l;
13 for(i=1;i<=num;i++)
14 for(j=1;j<=num;j++)
15 for(k=1;k<=num;k++)
16 for(l=1;l<=num;l++)
17 if(array[i][j]&&array[i][k]&&array[i][l]&&array[j][k]&&array[j][l]&&array[k][l])
18 {
19 printf("4 channels needed.\n");
20 return ;
21 }
22 for(i=1;i<=num;i++)
23 for(j=1;j<=num;j++)
24 for(k=1;k<=num;k++)
25 if(array[i][j]&& array[i][k]&&array[j][k])
26 {
27 printf("3 channels needed.\n");
28 return;
29 }
30 for(i=1;i<=num;i++)
31 for(j=1;j<=num;j++)
32 if(array[i][j])
33 {
34 printf("2 channels needed.\n");
35 return;
36 }
37 printf("1 channel needed.\n");
38 }
39
40 int main()
41 {
42 int i;
43 bool flag;
44 char ch,tch;
45 while(scanf("%d",&num)!=EOF)
46 {
47 if(num==0) break;
48 memset(array,false,sizeof(array));
49 flag=false;
50 getchar();
51 for(i=0;i<num;i++)
52 {
53 scanf("%c%c",&ch,&tch);
54 int a=ch-'A'+1;
55 while(scanf("%c",&ch)!=EOF)
56 {
57 if(ch=='\n') break;
58 int b=ch-'A'+1;
59 array[a][b]=true;
60 array[b][a]=true;
61 }
62 }
63 fuction();
64 }
65 return 0;
66 }

另一种方法是最大团,我用最大团做完之后发现,其实这个题用最大团的解法是错误的。比如:
5
A:BE
B:AC
C:BD
D:CE
E:AD
这组数据用最大团做,ans=2,但是这个题的答案应该是3.可见这个题的数据有问题,最大团的代码见下、

 View Code
View Code

1 #include <iostream>
2 #include <stdio.h>
3 #include <memory.h>
4 using namespace std;
5 //148K 0MS
6
7 const int maxnum=27;
8 bool array[maxnum][maxnum];
9 int use[maxnum];
10 int num,cn,bestn;
11
12
13 void dfs(int i)
14 {
15 if(i>num)
16 {
17 bestn=cn;
18 return ;
19 }
20 bool flag=true;
21 int j;
22 for(j=1;j<i;j++)
23 if(use[j] && !array[j][i])
24 {
25 flag=false;
26 break;
27 }
28 if(flag)
29 {
30 cn++;
31 use[i]=true;
32 dfs(i+1);
33 cn--;
34 use[i]=false;
35 }
36 if(cn+num-i>bestn)
37 {
38 use[i]=false;
39 dfs(i+1);
40 }
41 }
42
43 int main()
44 {
45 int i;
46 char ch,tch;
47 while(scanf("%d",&num)&& num!=0)
48 {
49 memset(array,false,sizeof(array));
50 memset(use,false,sizeof(use));
51 cn=0;
52 bestn=0;
53 getchar();
54 for(i=0;i<num;i++)
55 {
56 scanf("%c%c",&ch,&tch);
57 int a=ch-'A'+1;
58 while(scanf("%c",&ch) && ch!='\n')
59 {
60 int b=ch-'A'+1;
61 array[a][b]=true;
62 array[b][a]=true;
63 }
64 }
65 dfs(1);
66 if(bestn==1)
67 printf("1 channel needed.\n");
68 else
69 printf("%d channels needed.\n",bestn);
70 }
71 return 0;
72 }
73 /*
74 6
75 A:BEF
76 B:AC
77 C:BD
78 D:CEF
79 E:ADF
80 F:ADE
81 */

tju oj 1077
poj3692_最大团_二分图
题意:已知班级有g个女孩和b个男孩,所有女生之间都相互认识,所有男生之间也相互认识,给出m对关系表示哪个女孩与哪个男孩认识。现在要选择一些学生来组成一个团,使得里面所有人都认识,求此团最大人数。
思路:最大团问题。
定理:
原图的最大团=补图的最大独立集
原图的最大独立集=补图的最大团。
由于这个题的补图显然是一个二分图,而二分图的补图的最大独立集可以由匈牙利算法求的,所以该题的最大团问题可以转化成补图的最大独立集来做。
代码:

 View Code
View Code
1 #include <iostream>
2 #include <stdio.h>
3 #include <memory.h>
4 using namespace std;
5 const int maxnum=201;
6 bool array[maxnum][maxnum];
7 bool use[maxnum];
8 int res[maxnum];
9 int b,g,m;
10
11 bool find(int i)
12 {
13 int j;
14 for(j=1;j<=b;j++)
15 {
16 if(!use[j] && array[i][j])
17 {
18 use[j]=true;
19 if(res[j]==0 || find(res[j]))
20 {
21 res[j]=i;
22 return true;
23 }
24 }
25 }
26 return false;
27 }
28
29 int main()
30 {
31 int p,q;
32 int i,ans;
33 int k=0;
34 while(scanf("%d%d%d",&g,&b,&m)!=EOF)
35 {
36 if(g==0 && b==0 && m==0)
37 break;
38 memset(array,true,sizeof(array));
39 memset(res,0,sizeof(res));
40 for(i=0;i<m;i++)
41 {
42 scanf("%d%d",&p,&q);
43 array[p][q]=false; //补图
44 }
45 ans=0;
46 for(i=1;i<=g;i++)
47 {
48 memset(use,false,sizeof(use));
49 if(find(i))
50 ans++;
51 }
52 k++;
53 printf("Case %d: %d\n",k,b+g-ans);
54 }
55 return 0;
56 }
poj1419_染色_最大独立集_最大团
题意:
经典的图的染色问题,求对于给定的无向图中,给每个结点染两种不同颜色(黑色和白色)的一种且相邻结点的颜色不同,求染成黑色的最多结点数。
分析:
这个题求的图的最大独立集,最大独立集即为黑色节点的个数。
由于原图的最大独立集=补图的最大团。
而这个题是普通图,所以用回溯法来做,时间复杂度O(n*2^n)
代码:

 View Code
View Code

1 #include <iostream>
2 #include <memory.h>
3 #include <stdio.h>
4 using namespace std;
5
6 const int maxnum=101;
7 bool array[maxnum][maxnum];
8 bool use[maxnum]; //进入团的标号
9 bool bestx[maxnum];
10 int cn,bestn,p,e;
11
12 void dfs(int i)
13 {
14 int j;
15 bool flag;
16
17 if(i>p)
18 {
19 bestn=cn; //cn的值是递增的
20 // printf("%d\n",bestn);
21 // for(j=1;j<=p;j++)
22 // if(use[j])
23 // printf("%d ",j);
24 // printf("\n"); 在这里输出不一定是最大团
25 for(j=1;j<=p;j++) //而是应该赋值给另外一个数组,
26 bestx[j]=use[j];
27 return ;
28 }
29
30 flag=true;
31 for(j=1;j<i;j++)
32 if(use[j]&&!array[j][i])
33 {
34 flag=false;
35 break;
36 }
37 if(flag)
38 {
39 cn++;
40 use[i]=true;
41 dfs(i+1);
42 cn--;
43 }
44 if(cn+p-i>bestn) //剪枝
45 {
46 use[i]=false;
47 dfs(i+1);
48 }
49 }
50
51 int main()
52 {
53 int num,i,u,v;
54 scanf("%d",&num);
55 while(num--)
56 {
57 memset(array,true,sizeof(array));
58 memset(use,false,sizeof(use));
59 memset(bestx,false,sizeof(bestx));
60 scanf("%d%d",&p,&e);
61 for(i=0;i<e;i++)
62 {
63 scanf("%d%d",&u,&v);
64 array[u][v]=false;
65 array[v][u]=false;
66 }
67
68 cn=bestn=0;
69 dfs(1);
70 printf("%d\n",bestn);
71 for (i=1; i<=p; i++)
72 if(bestx[i])
73 printf("%d ",i);
74 printf("\n");
75 }
76
77 return 0;
78 }
79
80 /*
81 1
82 5 7
83 1 2
84 1 4
85 1 5
86 2 3
87 2 5
88 3 5
89 4 5
90 */
最大团
问题描述:团就是最大完全子图。
给定无向图G=(V,E)。如果U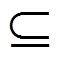 V,且对任意u,v
V,且对任意u,v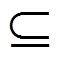 U 有(u,v)
U 有(u,v) 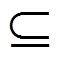 E,则称U 是G 的完全子图。
E,则称U 是G 的完全子图。
G 的完全子图U是G的团当且仅当U不包含在G 的更大的完全子图中,即U就是最大完全子图。
G 的最大团是指G中所含顶点数最多的团。
例如:


(a) (b) (c) (d)
图a是一个无向图,图b、c、d都是图a的团,且都是最大团。
求最大团的思路:
首先设最大团为一个空团,往其中加入一个顶点,然后依次考虑每个顶点,查看该顶点加入团之后仍然构成一个团,如果可以,考虑将该顶点加入团或者舍弃两种情况,如果不行,直接舍弃,然后递归判断下一顶点。对于无连接或者直接舍弃两种情况,在递归前,可采用剪枝策略来避免无效搜索。
为了判断当前顶点加入团之后是否仍是一个团,只需要考虑该顶点和团中顶点是否都有连接。
程序中采用了一个比较简单的剪枝策略,即如果剩余未考虑的顶点数加上团中顶点数不大于当前解的顶点数,可停止继续深度搜索,否则继续深度递归
当搜索到一个叶结点时,即可停止搜索,此时更新最优解和最优值。
以下是转载的某篇论文的,百度文库的
http://wenku.baidu.com/view/1bd93526a5e9856a561260e2.html
3.6 回溯法
3.6.1 算法基本思想
回溯法(Backtracking Algorithm, BA)有“通用的解题法”之称,用它可以系统地搜索一个问题的所有解或任一解,是一个既带有系统性又带有跳跃性的搜索算法。在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,总是先判断该结点是否肯定不包含问题的解,如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按照深度优先的策略进行搜索。BA在用来求问题的所有解时,要回溯到根,且根结点的所有子树都已被搜索遍才结束。而BA在用来求问题的任一解时,只要搜索到问题的一个解即可结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于解一些组合数较大的问题。
回溯法搜索解空间树时,根节点首先成为一个活结点,同时也成为当前的扩展节点。在当前扩展节点处,搜索向纵深方向移至一个新节点。这个新节点就成为一个新的活结点,并成为当前扩展节点。如果当前扩展节点不能再向纵深方向移动,则当前的扩展节点就成为死结点。此时,往回回溯至最近的一个活节点处,并使这个活结点成为当前的扩展节点。
回溯法以这种方式递归地在解空间中搜索,直至找到所有要求的解或解空间已无活结点为止。
3.6.2 算法设计思想
搜索:回溯法从根结点出发,按深度优先策略遍历解空间树,搜索满足约束条件的解。
剪枝:在搜索至树中任一结点时,先判断该结点对应的部分解是否满足约束条件,或者是否超出目标函数的界;也即判断该结点是否包含问题的解,如果肯定不包含,则跳过对以该结点为根的子树的搜索,即剪枝(Pruning);否则,进入以该结点为根的子树,继续按照深度优先的策略搜索。
一般来讲,回溯法求解问题的基本步骤如下:
(1) 针对所给问题,定义问题的解空间;
(2) 确定易于搜索的解空间结构;
(3) 以深度优先方式搜索解空间,并在搜索过程中利用Pruning函数剪去无效的搜索。
无向图G的最大团问题可以看作是图G的顶点集V的子集选取问题。因此可以用子集树表示问题的解空间。设当前扩展节点Z位于解空间树的第i层。在进入左子树前,必须确认从顶点i到已入选的顶点集中每一个顶点都有边相连。在进入右子树之前,必须确认还有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。
用邻接矩阵表示图G,n为G的顶点数,cn存储当前团的顶点数,bestn存储最大团的顶点数。cn+n-i为进入右子树的上界函数,当cn+n-i<bestn时,不能在右子树中找到更大的团,利用剪枝函数可将Z的右结点剪去。
3.6.3 实例分析
如图1所示,给定无向图G={V, E},其中V ={1,2,3,4,5},E={(1,2), (1,4), (1,5), (2,3), (2,5), (3,5), (4,5)}。根据MCP定义,子集{1,2}是图G的一个大小为2的完全子图,但不是一个团,因为它包含于G的更大的完全子图{1,2,5}之中。{1,2,5}是G的一个最大团。{1,4,5}和{2,3,5}也是G的最大团。
图2是无向图G的补图G'。根据最大独立集定义,{2,4}是G的一个空子图,同时也是G的一个最大独立集。虽然{1,2}也是G'的空子图,但它不是G'的独立集,因为它包含在G'的空子图{1,2,5}中。{1,2,5}是G'的最大独立集。{1,4,5}和{2,3,5}也是G'的最大独立集。

以图1为例,利用回溯法搜索其空间树,具体搜索过程(见图3所示)如下:假设我们按照1®2®3®4®5的顺序深度搜索。开始时,根结点R是唯一活结点,也是当前扩展结点,位于第1层,此时当前团的顶点数cn=0,最大团的顶点数bestn=0。在这个扩展结点处,我们假定R和第二层的顶点1之间有边相连,则沿纵深方向移至顶点1处。此时结点R和顶点1都是活结点,顶点1成为当前的扩展结点。此时当前团的顶点数cn=1,最大团的顶点数bestn=0。继续深度搜索至第3层顶点2处,此时顶点1和2有边相连,都是活结点,顶点2成为当前扩展结点。此时当前团的顶点数cn=2,最大团的顶点数bestn=0。再深度搜索至第4层顶点3处,由于顶点3和2有边相连但与顶点1无边相连,则利用剪枝函数剪去该枝,此时由于cn+n-i=2+5-4=3>bestn=0,则回溯到结点2处进入右子树,开始搜索。此时当前团的顶点数cn=2,最大团的顶点数bestn=0。再深度搜索至第5层顶点4处,由于顶点3和4无边相连,剪去该枝,回溯到结点3处进入右子树,此时当前团的顶点数cn=2,最大团的顶点数bestn=0。继续深度搜索至第6层顶点5处,由于顶点5和4有边相连,且与顶点1和2都有边相连,则进入左子树搜索。由于结点5是一个叶结点,故我们得到一个可行解,此时当前团的顶点数cn=3,最大团的顶点数bestn=3。vi的取值由顶点1至顶点5所唯一确定,即v=(1, 2, 5)。此时顶点5已不能再纵深扩展,成为死结点,我们返回到结点4处。由于此时cn+n-i=3+5-6=2<bestn=3,不能在右子树中找到更大的团,利用剪枝函数可将结点4的右结点剪去。以此回溯,直至根结点R再次成为当前的扩展结点,沿着右子树的纵深方向移动,直至遍历整个解空间。最后得到图1的按照1®2®3®4®5的顺序深度搜索的最大团为U={1,2,5}。当然{1,4,5}和{2,3,5}也是其最大团。
代码:

 View Code
View Code

1 #include <iostream>
2 #include <memory.h>
3 #include <stdio.h>
4 using namespace std;
5
6 const int maxnum=101;
7 bool array[maxnum][maxnum];
8 bool use[maxnum]; //进入团的标号
9 int cn,bestn,p,e;
10
11 void dfs(int i)
12 {
13 int j;
14 bool flag;
15
16 if(i>p)
17 {
18 bestn=cn;
19 printf("%d\n",bestn);
20 for(j=1;j<=p;j++)
21 if(use[j])
22 printf("%d ",j);
23 printf("\n");
24 return ;
25 }
26
27 flag=true;
28 for(j=1;j<i;j++)
29 if(use[j]&&!array[j][i])
30 {
31 flag=false;
32 break;
33 }
34 if(flag)
35 {
36 cn++;
37 use[i]=true;
38 dfs(i+1);
39 cn--;
40 }
41 if(cn+p-i>bestn) //剪枝
42 {
43 use[i]=false;
44 dfs(i+1);
45 }
46 }
47
48 int main()
49 {
50 int num,i,u,v;
51 scanf("%d",&num);
52 while(num--)
53 {
54 memset(array,false,sizeof(array));
55 memset(use,false,sizeof(use));
56 scanf("%d%d",&p,&e);
57 for(i=0;i<e;i++)
58 {
59 scanf("%d%d",&u,&v);
60 array[u][v]=true;
61 array[v][u]=true;
62 }
63
64 cn=bestn=0;
65 dfs(1);
66 //printf("%d\n",bestn);
67 }
68
69 return 0;
70 }
71
72 /*
73 1
74 5 7
75 1 2
76 1 4
77 1 5
78 2 3
79 2 5
80 3 5
81 4 5
82 */

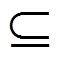 V,且对任意u,v
V,且对任意u,v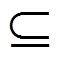 U 有(u,v)
U 有(u,v) 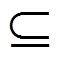 E,则称U 是G 的完全子图。
E,则称U 是G 的完全子图。







