逆序对之树形数组与归并排序
1.逆序对问题
逆序对，何为逆序对？逆序对就是在一序列array[]中，其中存在两个元素array[i]和array[j]，满足下列关系：
i<j其中i>=0 j<array.length 且 array[i]>array[j]，这一对数(array[i] , array[j])就是逆序对，要是给定一个任意的序列，那怎么求逆序对的数量呢？
求解该问题有两个经典的方案：
- 基于树状数组来求解
- 在归并排序的基础上求解
下面我们将慢慢介绍这两种算法：
2.逆序对之树状数组
2-1.树状数组
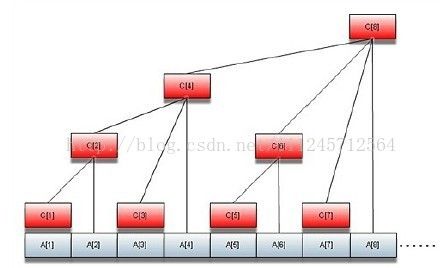
2-1-1.树状数组介绍
我们首先介绍一下什么是树状数组，树状数组顾名思义就是结构上长的很像树的数组，如下图：
图中这个红色的数组C[i](注意：下标从1开始)即为树状数组,下面的A[i]为一般的数组，C[i]是基于A[i]的基础上建立起来的，是为了来描述A[i]若干个连续元素之和，之间的对应的关系为：
C[1] = A[1]
C[2] = A[1]+A[2]
C[3] = A[3]
C[4] = A[1]+A[2]+A[3]+A[4]
C[5] = A[5]
...
C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+...+A[i]，里面的的lowbit()是什么呢？
我们不妨观察一下
| 十进制 | 二进制 | 尾部零的个数 | 对应层数 | 相加元素个数 |
| 1 | 1 | 0个 | 最底层 | 1(2^0) |
| 2 | 10 | 1个 | 倒数第二层 | 2(2^1) |
| 3 | 11 | 0个 | 最底层 | 1(2^0) |
| 4 | 100 | 2个 | 倒数第三层 | 4(2^2) |
| 5 | 101 | 0个 | 最底层 | 5(2^0) |
...
所以就设对应的数组下标为i，其二进制尾部零的个数为n，那么lowbit() = 2^n
2-1-2.树状数组的用途
由上面的分析可见，树状数组C[i]的值是A[i]里面的若干个连续的元素相加得到的，所以树状数组是用于在数组A中，里面的元素有可能不断的被更改，但是能高效的求出前数组A里面的前n项和，因为一般方法数组一旦更改了其中一个元素，比如A[0]被更改了，所有的前N项和都要更改，牵一发而动全身，而且更改代价为O(n^2)，那么有没有更快速的方法呢？有！那就是树状数组，可以在(nlogn)的代价内完成更改，下面慢慢道来。
2-1-3.树状数组的基本操作
lowbit(i)的求解
int lowbit(const int indexNumber)
{
return indexNumber&(-indexNumber);
//这里采用补码的思想
}
但是为什么是n~(-n)呢？
证明：假设n的二进制表示为：a1b其中‘1’是第一个‘1’ ，b表示全为零的部分，-n就表示成补码的形式（取反加一）A0B+1=A1b，于是n&(-n)=(a1b)&(A1b)，因为A，a互为反码，那么最后结果就为1b,即为2^n,证毕！
求前N项和
我们之前分析过C[i]=A[i]之间的对应关系，那么要是数组A的前N项和SUM[i]和C[i]之间有时什么关系呢？
SUM[1]=C[1];
SUM[2]=C[2];
SUM[3]=C[2]+C[3];
SUM[4]=C[4]；
SUM[5]=C[4]+C[5];
...
推出一般情况
SUM[i]=C[i]+C[i-lowbit(i)]+...+C[j](j>0)
代码如下：（因为树状数组要从1开始，那么我就将空出来的treeArray[0]存储树状数组的长度）
//计算前N1到N2之间的元素的和
int getSumN(const int treeArray[] ,int index)
{
if(index < 1 || index > treeArray[0])//treeArray[0]为树状数组的长度
{
fprintf(stderr, "%s\n","wrong array index" );
return 0;
}
int sum=0;
while(index > 0)
{
sum += treeArray[index];
index -= lowbit(index);
}
return sum;
}
树状数组更新操作
那要是A数组里面的一个元素A[i]发生了变化，那么对应的树状数组该如何变化呢？不妨回顾之前的A[i]和C[i]的对应关系，便可得知，一旦A[i]发生了变化，基于A[i]累加起来的树状数组的那些项都需要变化，从图上来看就是一旦一个儿子节点发生变化，其双亲节点直到根节点都需要加上变化值
// index表示更行的那个数组的索引
void updateTreeArray(int treeArray[],int index , const int value)
{
// 其中treeArray[0]表示了数组的长度
while(index <=treeArray[0])//将所有的父节点更新
{
treeArray[index]+=value;
index+=lowbit(index);
}
return ;
}
2-2.基于树状数组的逆序对求解
前面我们介绍了树状数组，现在我们开始正题
一开始我怎么都不会觉得树状数组和逆序对扯得上关系，后来网上查了一下，发现还真有巧妙的办法，树状数组最大的用途是什么？就是以nlogn的代价来求出前n项和，那么我们将序列里面的数一个一个的插入到初始化为0的树状数组C里面，每插入一个，那么就统计比自己小的元素有多少个（这里就是前N项和），并将插入位置i的A[i]加一，更新整个树状数组！这里理解起来有点抽象，那么我们就先抛开树状数组，假设有一序列inputArray {5,2,1,4,3}，有序列A{0,0,0,0,0}
A{0,0,0,0,0} ---插入5---> A{0,0,0,0,1}，现在比5小的数为0
A{0,0,0,0,1} ---插入2---> A{0,1,0,0,1}，现在有两个元素，但 是比2小的元素个数为0，那么说明比2大的元素有1个
A{0,1,0,0,1} ---插入1--->A{1,1,0,0,1}，现在有三个元素，但是比1小的元素为0，那么说明比1大的元素有2个
。。。以此类推
只不过我们将统计比当前元素小的元素个数交给了树状数组
要实现将树状数组求逆序对，要进行两个步骤：
树状数组完整代码请见文章末尾。
要实现将树状数组求逆序对，要进行两个步骤：
- 将输入数组离散化
- 离散化以后输入到一个树状数组里面，求逆序对数量
2-2-1.离散化
其实我们不将数组离散化也可以实现，但是因为树状数组对于下标有着严格的要求，一方面为了操作的方便，另一方面为了节省内存，所以我们选择将数组离散化，比如输入序列为{1,9999,10000},如果不离散化该数组，那么在树状数组里面将需要申请10000个节点元素，这样是不划算的,要是我们离散化该序列以后，那么输入序列将为{1,2,3}...这样节省了空间，又操作简便，下面给出离散化的步骤：
1.定义一个结构体
struct disrect_s
{
int value;//数组元素的值
int index;//数组元素位置标号
};
2.将输入数组的值赋值给一个struct disrect_s类型的数组
struct disrect_s disrectArray[arrayLength];
int i;
//赋值
for (i = 0; i < arrayLength; ++i)
{
disrectArray[i].value = inputArray[i];
disrectArray[i].index=i;
}
3.以value值排序disrectArray数组(注意这里排序一定要选一个nlogn代价的算法来排序，比如快排，归并排序等等，此处现则归并排序)
//以nlogn来排序 mergeSort(disrectArray , arrayLength);4.还原之前的标号，并将标号放入一个数组里面
int tempArray[arrayLength];
for(i=0 ; i<arrayLength ;++i)
{
tempArray[disrectArray[i].index]=i+1;
}
这个时候离散化完毕
比如输入一个数组为{9,1,0,5,4}，那么离散化就为{5,2,1,4,3}
2-2-2.将元素插入树状数组里面去
现在需要把temparray里面的元素从零开始一个一个的插入到树状数组里面去（注意数组的相对大小位置没有发生改变），具体代码如下：
int reversePairCount=0;
/*...*/
//一个一个的插入到树状数组里面去
createTreeArray(&treeArray,NULL,arrayLength);
for (i = 0; i < arrayLength; ++i)
{
// fprintf(stderr, "%s+++%d\n","Hello1",tempArray[i] );
updateTreeArray(treeArray,tempArray[i],1);
reversePairCount+=(i+1-getSumN(treeArray , tempArray[i]));//加上每个对应逆序对的数量
// fprintf(stderr, "%s\n","Hello2" );
}
//reversePairCount就是逆序对的数量
树状数组完整代码请见文章末尾。
3.逆序对之归并排序
现在要将的算法就比之前的树状数组简单不知多少了，也没有那么头疼了，在讲归并排序求逆序对之前我们不妨来看一个例子:
现在有序列A1={2,5,7,8} A2={1,4,6,9} A={A1,A2};其中A1升序，A2升序，那我们怎么来求解A里面的逆序对数量呢？因为A1升序，A2升序，所以A1，A2中不可能存在逆序对，那么逆序对(number1, number2)如果存在，那么只有可能一个输存在A1中,一个数存在A2中，现在只需要按顺序来取出A1,A2里面的元素来进行比较
在两个数组下标i,j都还未达到数组末尾时，两个比较无非又两种情况：
- A1[i]>A2[j],逆序对，那么此时将将reversePairCount++,然后++j;
- A1[i]<=A2[j]，非逆序对,++i；
当其中有一个数组为空时，也只有两种情况：
- i==A1.arrayLength;此时逆序对不可能存在了
- j==A2.arrayLength；剩余在A1里面的数全都是A2里面元素的的逆序对，既剩余个数为：reversePairCount+=(leftSubArrayLength-i-1)*rightSubArrayLength;
注意比较一下归并排序，归并排序的每一次操作都是基于上一次操作返回的两个有序的子序列上进行的，现在我们就在归并排序的过程中顺道解决一下逆序对的问题，具体代码如下：
#include <stdio.h>
#include <stdlib.h>
//通过归并排序来计算逆序对的数量
int MERGE(int subArray[] , const int left , const int right)
{
if(left >= right)
return 0;
int reversePairCount = 0;
int i ,j,k;
int center = (left+right)/2;
//计算左边和右边的逆序对的总数
reversePairCount+=MERGE(subArray , left , center);
reversePairCount+=MERGE(subArray , center+1 , right);
//左右边的子数组
const int leftSubArrayLength = center-left+1;
const int rightSubArrayLength = right-center;
int leftSubArray[leftSubArrayLength];
int rightSubArray[rightSubArrayLength];
for(i=0;i<leftSubArrayLength;++i)
{
leftSubArray[i]=subArray[left+i];
}
for(j=0;j<rightSubArrayLength;++j)
{
rightSubArray[j]=subArray[j+center+1];
}
i=0;j=0;k=0;
while(i<leftSubArrayLength && j<rightSubArrayLength)
{
if(leftSubArray[i]>rightSubArray[j])
{
subArray[k+left]=rightSubArray[j++];
reversePairCount++;
++k;
}
else
{
subArray[k+left]=leftSubArray[i++];
++k;
}
}
//辨别哪一个数组为空了
if(j==rightSubArrayLength)//右边数组空了
{
reversePairCount+=(leftSubArrayLength-i-1)*rightSubArrayLength;
while(i<leftSubArrayLength)
{
subArray[k+left] = leftSubArray[i];
++k;
++i;
}
}
else
{
while(j<rightSubArrayLength)
{
subArray[k+left]=rightSubArray[j];
++k;
++j;
}
}
//剩下的元素基体搬家
return reversePairCount;
}
int reversePair(const int inputArray[] , const int arrayLength)
{
int tempArray[arrayLength];//为了不破坏原数组的元素位置，申请一个新的数组
int i=0;
int count;
for(i=0;i<arrayLength ; ++i)
{
tempArray[i]=inputArray[i];
}
count=MERGE(tempArray , 0 , arrayLength-1);
for(i=0;i<arrayLength;++i)
{
printf("%d\t", tempArray[i]);
}
printf("\n" );
return count;
}
int main(int argc, char const *argv[])
{
int array[]={9,1,0,5,4};
printf("reverse pair number is:%d\n",reversePair(array , sizeof(array)/sizeof(int)));
return 0;
}
下面时树状数组求逆序对的代码：
treeArray.h
#ifndef _TREEARRAY_H
#define _TREEARRAY_H
//树状数组的通用接口
struct treeArray_t
{
int * node;
int treeLength;
};
typedef struct treeArray_t * TreeArray;
static int lowbit(const int number)
{
return number&(-number);
}
//创建一个数组并将其初始化
void createTreeArray( TreeArray * treeArrayPtr , const int inputArray[] , const int arrayLength);
//更新一个树状数组
void updateTreeArray(TreeArray treeArray ,int index , const int num );
//求前n项和的值
int getSumN(TreeArray treeArray , int index );
//销毁一个树状数组
void destoryTreeArray(TreeArray treeArray);
//打印一个treearray
void printTreeArray(const TreeArray treeArray);
#endif
treeArray.c
#include "treeArray.h"
#include <stdio.h>
#include <stdlib.h>
void createTreeArray(TreeArray * treeArrayPtr , const int inputArray[] , const int arrayLength)
{
if(arrayLength <=0)
{
fprintf(stderr, "%s\n", "array Length should greater than 0 " );
return;
}
int i=0;
(*treeArrayPtr) = (TreeArray)malloc(sizeof(struct treeArray_t));
if((*treeArrayPtr) == NULL)
{
fprintf(stderr, "%s\n","Out of space!");
exit(EXIT_FAILURE);
}
(*treeArrayPtr)->node = (int *)malloc(sizeof(int)*(arrayLength+1));
if((*treeArrayPtr)->node == NULL)
{
fprintf(stderr, "%s\n","Out of space!");
exit(EXIT_FAILURE);
}
(*treeArrayPtr)->treeLength = arrayLength+1;
//下面开始为树状数组赋值
if(inputArray == NULL)//默认将全部的树状数组初始化为0
{
for ( i = 1; i < (*treeArrayPtr)->treeLength; ++i)
{
(*treeArrayPtr)->node[i]=0;
}
}
else
{
for ( i = 1; i < (*treeArrayPtr)->treeLength; ++i)
{
int sum=0;
int j;
for ( j = i-lowbit(i)+1; j <=i; ++j)
{
sum+=inputArray[j-1];
}
(*treeArrayPtr)->node[i]=sum;
}
}
}
void updateTreeArray(TreeArray treeArray , int index ,const int num)
{
if(treeArray==NULL)
return;
while(index <= treeArray->treeLength)
{
treeArray->node[index]+=num;
index +=lowbit(index);
}
}
int getSumN(TreeArray treeArray , int index)
{
if(treeArray==NULL)
return;
int sum=0;
while(index >0)
{
sum+=treeArray->node[index];
index -=lowbit(index);
}
return sum;
}
void destoryTreeArray(TreeArray treeArray)
{
if(treeArray==NULL)
return;
free(treeArray->node);
free(treeArray);
treeArray=NULL;
}
void printTreeArray(const TreeArray treeArray)
{
if(treeArray==NULL)
return;
int i;
for (i = 1; i < treeArray->treeLength; ++i)
{
printf("%d\t",treeArray->node[i]);
// printf("%d\t",getSumN(treeArray , i));
fflush(stdout);
}
printf("\n");
}
reversePair.h
#ifndef _REVERSEPAIR_H
#define _REVERSEPAIR_H
#include "treeArray.h"
struct disrect_s
{
int value;
int index;
};
void MERGE(struct disrect_s subArray[] , const int left , const int right);
void mergeSort(struct disrect_s inputArray[] , const int arrayLength);
//计算逆序对的数量
int reverserPairNumber(const int inputArray[] , const int arrayLength);
#endif
reversePair.c
#include "reversePair.h"
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
void MERGE(struct disrect_s subArray[] , int left , int right)
{
if(left >= right)
return;
int mid = (left+right)/2;
MERGE(subArray , left , mid);
MERGE(subArray , mid+1 , right);
int i=0;
int j=0;
int k=0;
int leftSubArrayLength=mid-left+2;
int rightSubArrayLength = right-mid+1;
struct disrect_s leftSubArray[leftSubArrayLength];
struct disrect_s rightSubArray[rightSubArrayLength];
for(i=0;i<leftSubArrayLength-1;++i)
{
leftSubArray[i]=subArray[left+i];
}
for(j=0;j<rightSubArrayLength-1;++j)
{
rightSubArray[j]=subArray[mid+1+j];
}
leftSubArray[leftSubArrayLength-1].value=INT_MAX;
rightSubArray[rightSubArrayLength-1].value=INT_MAX;
//merge
i=0;
j=0;
for(k=left;k<=right;++k)
{
if(leftSubArray[i].value<=rightSubArray[j].value)
{
subArray[k]=leftSubArray[i];
++i;
}
else
{
subArray[k]=rightSubArray[j];
++j;
}
}
return;
}
void mergeSort(struct disrect_s inputArray[] , const int arrayLength)
{
MERGE(inputArray , 0 , arrayLength-1);
}
int reverserPairNumber(const int inputArray[] , const int arrayLength)
{
TreeArray treeArray=NULL;
struct disrect_s disrectArray[arrayLength];
int reversePairCount=0;
int tempArray[arrayLength];
int i;
//赋值
for (i = 0; i < arrayLength; ++i)
{
disrectArray[i].value = inputArray[i];
disrectArray[i].index=i;
}
//以nlogn来排序
mergeSort(disrectArray , arrayLength);
for(i=0 ; i<arrayLength ;++i)
{
tempArray[disrectArray[i].index]=i+1;
}
for (i = 0; i < arrayLength; ++i)
{
printf("%d\t", tempArray[i]);
}
//一个一个的插入到树状数组里面去
createTreeArray(&treeArray,NULL,arrayLength);
for (i = 0; i < arrayLength; ++i)
{
// fprintf(stderr, "%s+++%d\n","Hello1",tempArray[i] );
updateTreeArray(treeArray,tempArray[i],1);
reversePairCount+=(i+1-getSumN(treeArray , tempArray[i]));//加上每个对应逆序对的数量
// fprintf(stderr, "%s\n","Hello2" );
}
return reversePairCount;
}
main.c
#include <stdio.h>
#include <stdlib.h>
#include "treeArray.h"
#include "reversePair.h"
int main(int argc, char const *argv[])
{
int array[]={9,1,0,5,4};
printf("reversePair number is:%d\n",reverserPairNumber(array, sizeof(array)/sizeof(int)) );
return 0;
}
makefile
<span style="font-size:18px;">main:treeArray.o main.o reversePair.o gcc treeArray.o main.o reversePair.o -o main.exe treeArray.o:treeArray.h main.o:treeArray.h reversePair.h reversePair.o:reversePair.h .PHONY:clean clean: rm -f *.o *.exe</span>