【数据结构】常见的7种比较排序算法2

● 快速排序（Quick Sort）

1、算法描述：

   在平均状况下，排序n个数据要O(nlg(n))次比较。在最坏状况下则需要O(n^2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他O(nlg(n))算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，且在大部分真实世界的数据，可以决定设计的选择，减少所需时间的二次方项的可能性。

2、步骤：

1）从数列中挑出一个元素，称为 “基准”。

2）重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区操作。

3）递归把小于基准值元素的子数列和大于基准值元素的子数列排序。

算法优化：

1）如果进行排序的区间较小，快速排序效率较低，可通过插入排序实现

2）对于基准的选取，利用三数取中法，就不会恰好取到最大或最小的数，避免了最快情况的发生

三数取中法（首位、中间和末尾的数据）

int GetMidOfThree(int *arr, int left, int mid, int right)//三数取中法（left，mid和right所在数据中取中间数作为“基准”）
{
 assert(arr);
 if (arr[left] < arr[mid])
 {
  if (arr[mid] < arr[right])
  {
   return arr[mid];
  }
  else //arr[right]<=arr[mid]
  {
   if (arr[left] > arr[right])
    return arr[left];
   else
    return arr[right];
  }
 }
 else//arr[left]>=arr[mid]
 {
  if (arr[mid] > arr[right])
  {
   return arr[mid];
  }
  else//arr[right]>=arr[mid]
  {
   if (arr[right] > arr[left])
    return arr[left];
   else
    return arr[right];
  }
 }
}

对于步骤2，有三种实现方式

int PartSort1(int *arr, int left, int right)//方法一
{//使右边均为大于key的数，左边均为小于key的数
 assert(arr);
 int key = GetMidOfThree(arr, left, left - (left - right) / 2, right);//选取“基准”下标
 //int key = arr[left];//也可为right
 int begin = left;
 int end = right;
 while (begin < end)
 {
  while (begin < end && arr[begin] <= key)//从左往右找大于key的数
  {
   begin++;
  }
  while (begin < end && arr[end] >= key)//从右往左找小于key的数
  {
   end--;
  }
  if (begin < end)//如果begin<end进行交换,相等也可以交换，故该if条件可以不写
  {
   swap(arr[begin], arr[end]);
  }
 }
 //此时begin和end相等
 if (arr[begin] > arr[right])//处理只有两个数时eg:2 1;
 {
  swap(arr[begin], arr[right]);
 }
 return end;
}
int PartSort2(int *arr, int left, int right)//方法二：挖坑法
{
 assert(arr);
 //基准为left数据，在进行循环时先进行右边查找，再进行左边查找；基准为right时，顺序相反
 //这样才能将比key大的数存放在前一部分，比key小的存放在后一部分
 //不能用三数取中法选取基准【仅是个人观点，如有误请多多指教】
 int key = arr[left];
 int begin = left;
 int end = right;//此处从right处开始
 while (begin < end)
 {
  while (begin < end && arr[end] >= key)//右边找比key小的数据
  {
   end--;
  }
  if (begin < end)
  {
   arr[begin++] = arr[end];
  }
  while (begin < end && arr[begin] <= key)//左边找比key大的数据
  {
   begin++;
  }
  if (begin < end)//埋坑。（end--）挖新坑
  {
   arr[end--] = arr[begin];
  }
 }
 arr[begin] = key;
 return end;
}
int PartSort3(int *arr, int left, int right)//方法三：此法更好些(代码简单)，通过prev和cur遍历一次进行排序
{
 int key = arr[right];//不能用三数取中进行，如果key为arr[left],则循环从后往前进行，找大于key的数进行交换
 int prev = left - 1;
 int cur = left;
 while (cur < right)//从左往右遇大于或等于key的数，跳过去；遇到小于key的数停下来进行交换
 {//prev的两种情况：1、紧跟在cur后面；2、指向比key大的前一个数
  if (arr[cur] < key && ++prev != cur)//如果prev和cur紧跟就不进行交换
  {
   swap(arr[cur], arr[prev]);
  }
  cur++;
 }
 swap(arr[++prev], arr[right]);//将prev的后一位与最后元素进行交换
 return prev;
}

递归函数的实现

void QuickSort(int *arr, int left, int right)
{
 assert(arr);
 if (left >= right)//递归退出条件
 {
  return;
 }
 if (right - left < 13)//当区间比较小时，用插入排序（提高性能）
 {
  InsertSort(arr, right - left);
 }
 //int div = PartSort1(arr, left, right);
 //int div = PartSort2(arr, left, right);
 int div = PartSort3(arr, left, right);
 QuickSort(arr, left, div - 1);
 QuickSort(arr, div + 1, right);
}

非递归实现快速排序

void QuickSort_NonR(int *arr, int left, int right)//快速排序---非递归法(利用栈)
{
 assert(arr);
 stack<int> s;
 if (left < right)//两端数据入栈,right先入栈，left后入栈
 {
  s.push(right);
  s.push(left);
 }
 while (left < right && !s.empty())
 {
  //取出要进行数据段的两端
  left = s.top();
  s.pop();
  right = s.top();
  s.pop();
  if (left - right < 13)
  {
   InsertSort(arr, left - right + 1);
  }
  else
  {
      int div = PartSort3(arr, left, right);//循环进行，div的右边后入栈，先进行右边的排序
   if (left < div - 1)
   {
    s.push(div - 1);
    s.push(left);
   }
   if (right > div + 1)
   {
    s.push(right);
    s.push(div + 1);
   }
  }
 }
}

● 归并排序（Merg Sort）

1、算法描述：

     归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用

2、步骤：

1）申请和原序列一样大的空间，该空间用来存放合并后的序列

2）序列分为两部分，进行递归，先使小的序列有序，在回退使较大序列有序

3）进行两个序列的合并后，将有序序列回写到原序列中

具体实现如下：

void _Merg(int *arr, int *tmp, int begin1, int end1, int begin2, int end2)//进行两个序列的合并
{
 assert(arr);
 assert(tmp);
 int index = begin1;
 while (begin1 <= end1 && begin2 <= end2)
 {
  if (arr[begin1] < arr[begin2])//小的数据写入tmp
  {
   tmp[index] = arr[begin1];
   begin1++;
  }
  else
  {
   tmp[index] = arr[begin2];
   begin2++;
  }
  index++;
 }
 //数据多序列的链接在tmp后面
 while (begin1 <= end1)
 {
  tmp[index++] = arr[begin1++];
 }
 while (begin2 <= end2)
 {
  tmp[index++] = arr[begin2++];
 }
}
void _MergSort(int *arr, int *tmp, int left, int right)//递归使要进行合并的序列有序，再调用合并序列函数
{
 assert(arr);
 assert(tmp);
 if (left >= right)
 {
  return;
 }
 int mid = left - (left - right) / 2;
 _MergSort(arr, tmp, left, mid);
 _MergSort(arr, tmp, mid + 1, right);
 //合并后回写到arr中
 _Merg(arr, tmp, left, mid, mid + 1, right);
 for (int i = left; i <= right; i++)
 {
  arr[i] = tmp[i];
 }
}
void MergSort(int *arr, int size)
{
 assert(arr);
 int *tmp = new int[size];//开辟size空间tmp临时存放部分合并的数据
 memset(tmp, 0, size*sizeof(int));//初始化
 _MergSort(arr, tmp, 0, size - 1);
 delete[] tmp;
}

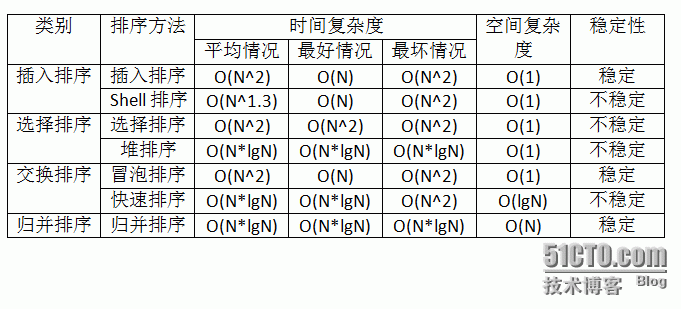
对于这7种算法的复杂度和稳定性的总结