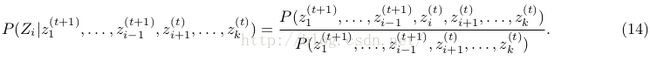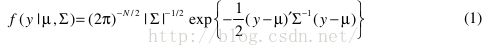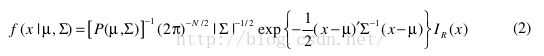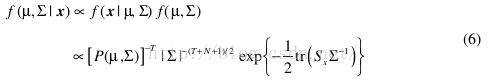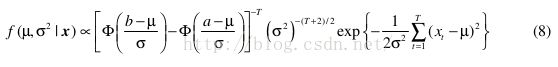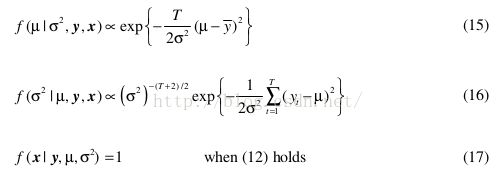随机采样和随机模拟：吉布斯采样Gibbs Sampling的具体实现

http://blog.csdn.net/pipisorry/article/details/51539739

吉布斯采样的实现问题

本文主要说明如何通过吉布斯采样来采样截断多维高斯分布的参数（已知一堆截断高斯分布的数据，推断其参数( μ , Σ )）。

关于吉布斯采样的介绍文章都停止在吉布斯采样的详细描述上，如随机采样和随机模拟：吉布斯采样Gibbs Sampling(why)但并没有说明吉布斯采样到底如何实现的(how)？

也就是具体怎么实现从下面这个公式采样？

下面介绍如何为多维正态分布构建一个吉布斯采样器，来采样截断多维高斯分布的参数。

皮皮blog

模型的表示

y为均值为μ协方差矩阵为 Σ的( N × 1)正态随机向量，其概率密度函数pdf为：

[概率论：高斯分布]

假设x是y的截断truncated版本，有同样的参数location and scale parameters μ and Σ , 只是截断到区域 R = { ( a i < x i < b i ), i = 1,2,... N } ，(a 可以为 −∞ or b 可以为 +∞ )。

x的pdf为：

I R ( x )是指示器函数：当x在区域R中时值为1，否则为0；

P ( μ , Σ ) ]− 1是正则化常数（由于截断），为

让 x = ( x 1 , x 2 ,..., x T ) 表示截断多维高斯分布pdf f ( x | μ , Σ ) 的随机采样

则随机采样x的pdf（μ 和 Σ的似然函数）为

高斯分布的先验和数据产生后验分布

As a prior pdf for ( μ , Σ ) , we will use the conventional noninformative diffuse prior (see, for example, Zellner 1971, p.225)

Combining this prior with the likelihood function yields the posterior pdf for ( μ , Σ )

得到后验分布后，我们可以从这些后验pdfs中采样，并利用这些采样值估计边缘后验分布和矩（moments）。

然而其中的和式没法消去，后面将介绍如何利用隐含变量消去它。

皮皮blog

单变量高斯分布The Univariate Case

单变量高斯分布中，正则化因子式3变为：

where Φ (.) is the standard normal cumulative distribution function (cdf).

(μ , σ 2)的后验pdf (式6)为

然而从上式没法得到f ( σ 2 | x ) and f ( μ | x )：It is not possible to analytically integrate out μ or σ 2 from this pdf to obtain the marginal posterior pdfs f ( σ 2 | x ) and f ( μ | x ) . Also, because the conditional posterior pdfs f ( σ 2 | μ , x ) and f ( μ | σ 2 , x ) are not recognisable, it is not possible to set up a Gibbs’ sampling algorithm that draws from these conditional pdfs.

所以我们添加对应x的隐含变量y：令y = ( y 1 , y 2 ,..., y T ) ′ ， 可看作非截断正态分布N ( μ , σ 2 )的采样，并且和截断观测值x有直接的（确定性的deterministic）对应。

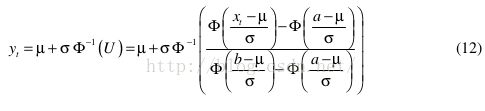
考虑采样观测值y t from N ( μ , σ 2 )和x t from N ( μ , σ 2 ) × I ( a , b ) ( x t )的逆累积分布函数（inverse cdf）方法：

给定均匀分布抽样Ufrom (0,1)，y t and x t的抽样分别为：

。。。一堆推导（略）

得到x和y之间的确定deterministic关系

根据贝叶斯理论，我们可以重写μ , σ 2 and y的联合后验分布（joint posterior pdf）为

由于f ( x | y , μ , σ 2 ) = 1 when (12) holds, and is zero otherwise.     The remaining terms on the right side of (13) involve y not x.则

where y is the sample mean of the y t and the relationship between y and x is given by (12).

式14中，吉布斯采样需要的条件后验pdfs分别为：

式16：Inverse-gamma distribution

综上，

吉布斯采样截断高斯分布参数算法

从后验pdf中生成( μ , σ 2 )的步骤为

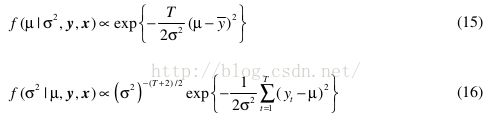
皮皮blog

同步图计算并行化处理

lz的不一定正确。。。

使用已有方法产生截断高斯分布的数据点，将数据分成M份，分布在M个worker节点中。

超步1：所有节点运行吉布斯采样截断高斯分布参数算法，得到部分训练数据的参数采样结果( μ , σ 2 )（局部模型）

超步2+：

每个节点收到其它节点发来的( μ , σ 2 )信息，重新计算( μ , σ 2 )（全局模型，替换局部模型）

所有节点重新运行吉布斯采样截断高斯分布参数算法，得到部分训练数据的参数采样结果( μ , σ 2 )

burn-in阶段将得到的最后一个采样结果( μ , σ 2 )发送给所有其它节点；收敛阶段将得到的采样结果( μ , σ 2 )的均值发送给所有其它节点。

每隔几个Gibbs sampling迭代结束超步进行同步，并准备进入下一个超步。

[Distributed Inference for Latent Dirichlet Allocation]

最后lz有一个问题，吉布斯采样能用在连续的n维高斯分布采样中吗？如果可以如何实现，马尔可夫毯？

from: http://blog.csdn.net/pipisorry/article/details/51539739

ref: