java常用排序算法
在各类算法中,排序算法是最基本的内容。在这里主要分享一个冒泡排序,选择排序,插入排序,希尔排序,快速排序和堆排序以及合并排序。
1、冒泡排序
这里是最基础的了,不用多说。
public static void bubbleSort(int[] a){
int temp;
for(int i=1;i<a.length;i++){
for(int j=0;j<a.length-i;j++){
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
System.out.print("第"+i+"步排序结果是:");
for(int k=0;k<a.length;k++){
System.out.print("\t"+a[k]);
}
System.out.print("\n");
}
}
2、选择排序
主要是通过选择和交换来实现排序,长得和冒泡差不多
public static void selectSort(int[] a){
int index,temp;
for(int i=0;i<a.length-1;i++){
index=i;
for(int j=i+1;j<a.length;j++){
if(a[j]>a[index]){
index=j;
}
}
if(index!=i){
temp=a[i];
a[i]=a[index];
a[index]=temp;
}
System.out.print("第"+i+"步排序结果是:");
for(int k=0;k<a.length;k++){
System.out.print("\t"+a[k]);
}
System.out.print("\n");
}
}
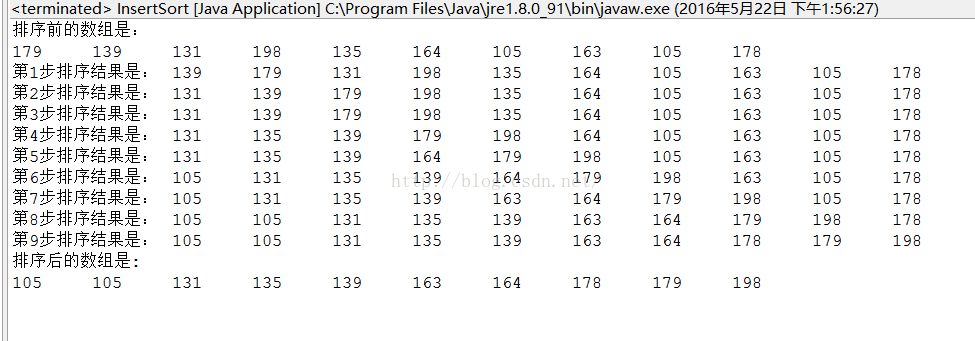
主要是通过对未排序的数据执行逐个插入至合适的位置而完成排序工作。
static void insertionSort(int[] a ){
int i,j,t,h;
for(i=1;i<a.length;i++){
t=a[i];
j=i-1;
while(j>=0 && t<a[j]){
a[j+1]=a[j];
j--;
}
a[j+1]=t;
System.out.print("第"+i+"步排序结果是:");
for(int k=0;k<a.length;k++){
System.out.print("\t"+a[k]);
}
System.out.print("\n");
}
}
4、希尔排序
基于插入排序的思想,主要是将n个元素分成n/2个数字序列,第1个数据和第n/2+1个数据为一对,一次循环使每一个序列对排好顺序,然后再变为n/4个序列,再次排序,除的时候取整。
static void shellSort(int[] a ){
int i,j,h;
int r,temp;
int x=0;
for(r=a.length/2;r>=1;r/=2){
for(i=r;i<a.length;i++){
temp=a[i];
j=i-r;
while(j>=0 && temp<a[j]){
a[j+r]=a[j];
j-=r;
}
a[j+r]=temp;
}
x++;
System.out.print("第"+x+"步排序结果是:");
for(h=0;h<a.length;h++){
System.out.print("\t"+a[h]);
}
System.out.print("\n");
}
}
5、快速排序
快速排序通过多次比较和交换来实现排序,首先设定一个分界值,通过该分界值的数据分为左右两部分,将大于等于分界值的数据集中到数组右边,小于的放到数组左边。然后左右两边的数据可以独立排序。重复上述过程。
static void quickSort(int[] arr,int left,int right){
int f,t;
int rtemp,ltemp;
ltemp=left;
rtemp=right;
f=arr[(left+right)/2];
while(ltemp<rtemp){
while(arr[ltemp]<f){
++ltemp;
}
while(arr[rtemp]>f){
--rtemp;
}
if(ltemp<=rtemp){
t=arr[ltemp];
arr[ltemp]=arr[rtemp];
arr[rtemp]=t;
--rtemp;
++ltemp;
}
}
if(ltemp==rtemp){
ltemp++;
}
if(left<rtemp){
quickSort(arr,left,ltemp-1);
}
if(ltemp<right){
quickSort(arr,rtemp+1,right);
}
}

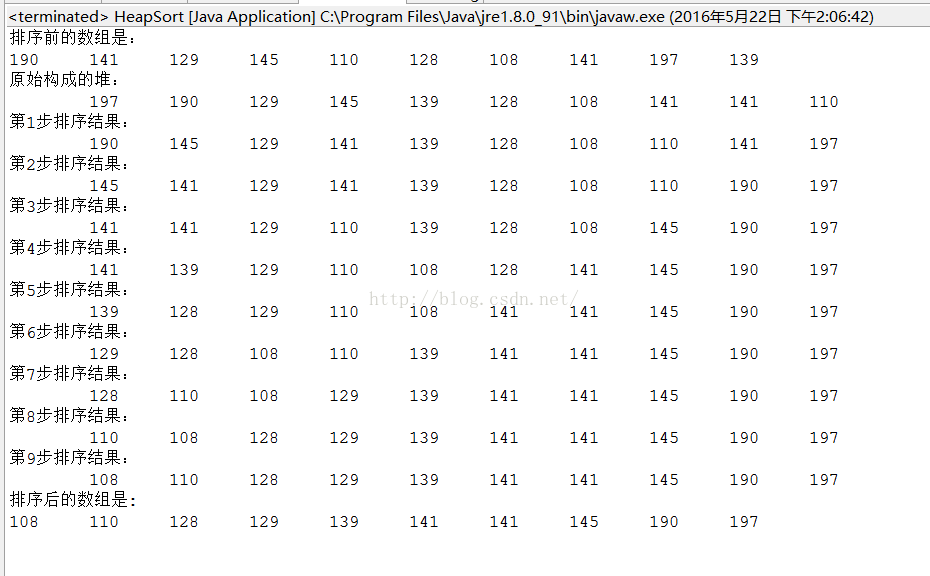
6、堆排序
这个就稍稍有点复杂了哦。
一个完整的堆排序需要经过反复的两个步骤:构造堆结构和堆排序输出。
首先将原始的无序数据放置到一个完全二叉树的各个结点中,然后由完全二叉树的下层向上层逐层对父子结点的数据进行比较,
使父结点的数据大于子结点的数据。这里需要使用筛运算进行结点数据的调整,直到所有结点最后都满足堆结构的条件为止。
static void heapSort(int a[],int n){ //堆排序
int i,j,h,k;
int t;
for(i=n/2-1;i>=0;i--){ //将a[0,n-1]建成大根堆
while(2*i+1<n){ //第i个结点有右子树
j=2*i+1;
if((j+1)<n){
if(a[j]<a[j+1]) //右左子树小于右子树,则需要比较右子树
j++; //序号增加1,指向右子树
}
if(a[i]<a[j]){ //比较i与j为序号的数据
t=a[i]; //交换数据
a[i]=a[j];
a[j]=t; //堆被破坏,需要重新调整
i=j;
}
else{ //比较左右子树均大则堆未破坏,不再需要调整
break;
}
}
}
System.out.println("原始构成的堆:");
for(h=0;h<n;h++){
System.out.print("\t"+a[h]);
}
System.out.print("\n");
for(i=n-1;i>0;i--){
t=a[0]; //与第i个记录交换
a[0]=a[i];
a[i]=t;
k=0;
while(2*k+1<i){ //第i个结点有右子树
j=2*k+1;
if((j+1)<i){
if(a[j]<a[j+1]){ //右左子树小于右子树,则需要比较右子树
j++; //序号增加1,指向右子树
}
}
if(a[k]<a[j]){ //比较i与j序号的数据
t=a[k]; //交换数据
a[k]=a[j];
a[j]=t;
k=j; //堆被破坏,需要重新调整
}else{
break;
}
}
System.out.println("第"+(n-i)+"步排序结果:");
for(h=0;h<n;h++){
System.out.print("\t"+a[h]);
}
System.out.print("\n");
}
}
/**
* 参数a是以线性方式保存的二叉树数组,输入参数n为数组的长度。
*
* @param args
*/
7、合并排序
一个待排序的原始数据排序进行合并排序的基本思路:首先将含有n个结点的待排序数据序列看成是由n个长度为1的有序子表组成,
* 将其依次两两合并,得到长度为2的若干有序子表;然后,再对
static void mergeOne(int a[],int b[],int n ,int len){ //完成一次合并的函数
int i,j,k,s,e;
s=0;
while(s+len<n){
e=s+2*len-1;
if(e>=n){ //最后一段可能少于len个结点
e=n-1;
}
//相邻有序段合并
k=s;
i=s;
j=s+len;
while(i<s+len && j<=e){ //如果两个有序表都未结束时,循环比较
if(a[i]<=a[j]){ //如果较小的元素复制到数组b中
b[k++]=a[i++];
}else{
b[k++]=a[j++];
}
}
while(i<s+len){ //未合并的部分复制到数组b中
b[k++]=a[i++];
}
while(j<=e){
b[k++]=a[j++]; //未合并的部分复制到数组b中
}
s=e+1; //下一对有序段中左段的开始下标
}
if(s<n){ //将剩余的一个有序段从数组A复制到数组b中
for(;s<n;s++){
b[s]=a[s];
}
}
}
static void mergeSort(int a[],int n){ //合并排序
int h,count,len,f;
count=0; //排序步骤
len=1; //有序序列长度
f=0; //变量f做标志
int[] p=new int[n];
while(len<n){
if(f==1){ //交替在A和P之间合并
mergeOne(p,a,n,len); //p合并到a
}else{
mergeOne(a,p,n,len); //a合并到p
}
len=len*2; //增加有序序列长度
f=1-f; //使f值在0和1之间切换
count++;
System.out.printf("第"+count+"排序结果:");
for(h=0;h<SIZE;h++){
System.out.print("\t"+a[h]);
}
System.out.print("\n");
}
if(f==1){ //如果进行了排序
for(h=0;h<n;h++){ //将内存p中的数据复制回数组a
a[h]=p[h];
}
}
}
/**
* 在MergeOne()方法中,输入参数a是一个数组,用来保存待排序的数据,输入参数b是一个数组,用来保存合并后的数据
* ,参数n表示数组a中需要进行排序的元素总数,参数len表示每个有序子表的长度。
*
* 二路合并排序算法需要申请较大的辅助内存空间,这个辅助空间的大小与待排序的原始序列一样多。
*
*
* @param args
*/

在这里分享的集中排序算法中,冒泡排序,插入排序和合并排序都是稳定排序算法(即维持记录的相对次序来进行排序)。
没有一种排序算法是绝对好坏的,不同的排序算法各有优劣,在实际应用中药按实际情况来选择排序算法。如果数据量较小,可以采用插入排序或者选择排序,当数据量n较大时,则应该用时间复杂度为O(nlogn)的排序方法,如快速排序,堆排序或合并排序,用空间换时间。如果排序的原始数据呈随机分布,则用快速排序。
源码下载地址:点击打开链接http://download.csdn.net/detail/sdksdk0/9527723
