栈和队列基础知识
栈和队列也是线性表,其特殊性在于栈和队列的基本操作是线性表操作的子集,它们是操作受限的线性表,因此,可称为限定性的数据结构。但从数据类型角度看,它们是和线性表大不相同的两类重要的抽象数据类型。
栈
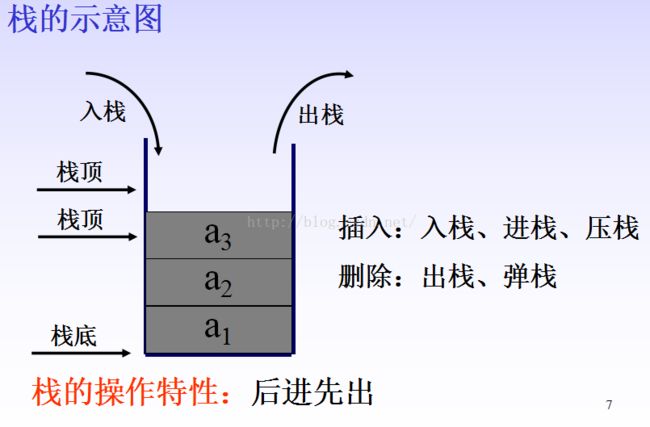
栈是限定仅在表尾进行插入或删除操作的线性表。因此,对栈来说,表尾端有其特殊含义,称为栈顶,相应地,表头端称为栈底。不含元素的空表称为空栈。
栈又称为后进先出的线性表(简称LIFO结构)。
栈的抽象数据类型定义
ADT Stack {
数据对象:
D={ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 }
数据关系:
R1={ <ai-1 ,ai >|ai-1 ,ai∈D, i=2,...,n } 约定an端为栈顶,a1端为栈底
基本操作:
}ADT Stack
InitStack (&S) (构造空栈 ) 操作结果:构造一个空栈S。
DestroyStack(&S) (销毁栈结构) 初始条件:栈S已存在。 操作结果:栈S被销毁。
ClearStack (&S) (栈清空) 初始条件:栈S已存在。 操作结果:栈S清为空栈。
StackEmpty (S) (判空) 初始条件:栈S已存在。 操作结果:若栈S为空栈,则返回TRUE, 否则FALSE。
StackLength (S) (求栈长) 初始条件:栈S已存在。 操作结果:返回S的元素个数,即栈的长度。
StackTraverse (S, visit( )) (遍历栈) 初始条件:栈S已存在且非空。 操作结果:从栈底到栈顶依次对S的每个数据元素调 用函数visit()。一旦visit()失败,则操作失效。
GetTop (S, &e) (求栈顶元素) 初始条件:栈S已存在且非空。 操作结果:用e返回S的栈顶元素。
Push (&S, e) (入栈) 初始条件:栈S已存在。 操作结果:插入元素e为新的栈顶元素。
Pop (&S, &e) (出栈) 初始条件:栈S已存在且非空。 操作结果:删除S的栈顶元素,并用e返回其值。
栈的表示和实现
和线性表类似,栈也有两种存储表示方法。
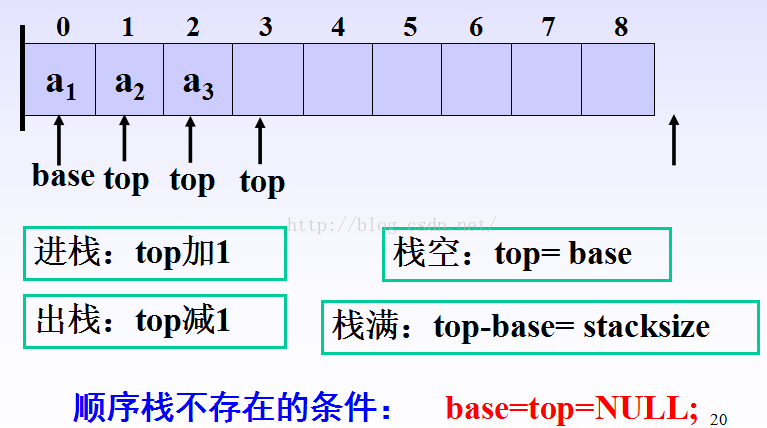
顺序栈,即栈的顺序存储结构是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置。base可称为栈底指针,在顺序栈中,它始终指向栈底的位置,若base的值为NULL,则表明栈结构不存在。称top为栈顶指针,其初始值指向栈底,即top=base可以作为栈空的标记。每当插入新的栈顶元素时,指针top增1,删除栈顶元素时,指针top减1,因此,非空栈中的栈顶指针始终在栈顶元素的下一个位置上。

链栈:由于栈的操作是线性表操作的特例,则链栈易于实现,在此不做详细讨论。
说明:
① 链栈不必设头结点,因为栈顶(表头)操作频繁; ②采用链栈存储方式,可使多个栈共享空间;当栈中元素个数变化较大,且存在多个栈的情况下,链栈是栈的首选存储方式。
顺序栈和链栈的比较
时间性能:相同,都是常数时间O(1)。
空间性能:
顺序栈:有元素个数的限制和空间浪费的问题。
链栈:没有栈满的问题,只有当内存没有可用空间时才会出现栈满,但是每个元素都需要一个指针域,从而产生了结构性开销。
总之,当栈的使用过程中元素个数变化较大时,用链栈是适宜的,反之,应该采用顺序栈。
栈应用举例:数制转换,括号匹配,行编辑程序,迷宫求解,表达式求值,递归的实现等
队列
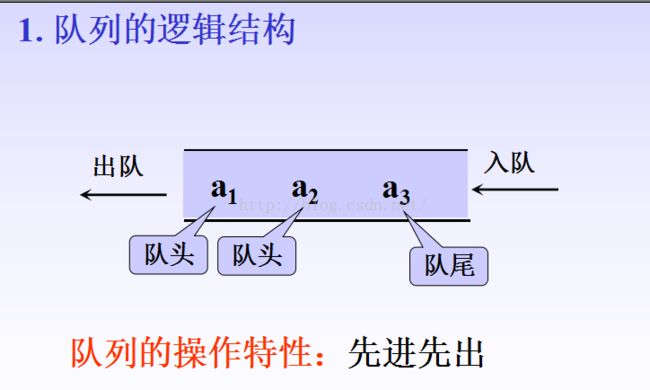
和栈相反,队列是一种先进先出(FIFO)的线性表。它只允许在表的一端进行插入,而在另一端删除元素。在队列中允许插入的一端叫队尾,允许删除的一端则称为队头。
双端队列是限定插入和删除操作在表的两端进行的线性表。这两端分别称作端点1和端点2,也可以像栈一样,可以用一个铁道转轨网络来比喻双端队列。在实际使用中,还可以有输出受限的双端队列(即:一个端点允许插入和删除,另一个端点只允许插入的双端队列)和输入受限的双端队列(即一个端点允许插入和删除,另一个端点只允许删除的双端队列)。而如果限定双端队列从某个点插入的元素只能从该端点删除,则该双端队列就蜕变为两个栈底相邻接的栈了。尽管双端队列看起来似乎比栈和队列更灵活,但实际上在应用程序中远不及栈和队列有用。
队列的链式存储结构及实现


队列的抽象数据类型定义 :
ADT Queue {
数据对象:
D={ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 }
数据关系:
R1={ <ai-1 ,ai >|ai-1 ,ai∈D, i=2,...,n } 约定an端为队尾,a1端为队头
基本操作:
}ADT Queue
InitQueue (&Q) (构造空队列 ) 操作结果:构造一个空队列Q。
DestroyQueue (&Q) (销毁队列结构) 初始条件:队列Q已存在。 操作结果:队列Q被销毁。
ClearQueue (&Q) (队列清空) 初始条件:队列Q已存在。 操作结果:队列Q清为空队列。
QueueEmpty (Q) (判空) 初始条件:队列Q已存在。 操作结果:若队列Q为空,则返回TRUE, 否则FALSE。
QueueLength (Q) (求队列长) 初始条件:队列Q已存在。 操作结果:返回Q的元素个数,即队列的长度。
QueueTraverse (Q, visit( )) (遍历队列) 初始条件:队列Q已存在且非空。 操作结果:从队头到队尾,依次对Q的每个数据元素 调用函数visit()。一旦visit()失败,则操作失效。
GetHead (Q, &e) (求队头元素) 初始条件:队列Q已存在且非空。 操作结果:用e返回Q的队头元素。
EnQueue (&Q, e) (入队) 初始条件:队列Q已存在。 操作结果:插入元素e为新的队头元素。
DeQueue (&Q, &e) (出队) 初始条件:队列Q已存在且非空。 操作结果:删除Q的队头元素,并用e返回其值。
除了栈和队列之外,还有一种限定性数据结构是双端队列。
双端队列是限定插入和删除操作在表的两端进行的线性表。这两端分别称作端点1和端点2,也可以像栈一样,可以用一个铁道转轨网络来比喻双端队列。在实际使用中,还可以有输出受限的双端队列(即:一个端点允许插入和删除,另一个端点只允许插入的双端队列)和输入受限的双端队列(即一个端点允许插入和删除,另一个端点只允许删除的双端队列)。而如果限定双端队列从某个点插入的元素只能从该端点删除,则该双端队列就蜕变为两个栈底相邻接的栈了。尽管双端队列看起来似乎比栈和队列更灵活,但实际上在应用程序中远不及栈和队列有用。
队列的链式存储结构及实现

如何改进出队的时间性能?
放宽队列的所有元素必须存储在数组的前n个单元这一条件 ,只要求队列的元素存储在数组中连续的位置。
设置队头、队尾两个指针
如何确定不同的队空、队满的判定条件? 为什么要将队空和队满的判定条件分开?
方法一:附设一个存储队列中元素个数的变量num, 当num=0时队空,当num=QueueSize时为队满;
方法二:修改队满条件,浪费一个元素空间,队满时数组中只有一个空闲单元;
方法三:设置标志flag,当front=rear且flag=0时为队空,当front=rear且flag=1时为队满。
循环队列和链队列的比较:
时间性能: 循环队列和链队列的基本操作都需要常数时间O (1)。
空间性能: 循环队列:必须预先确定一个固定的长度,所以有存储元素个数的限制和空间浪费的问题。 链队列:没有队列满的问题,只有当内存没有可用空间时才会出现队列满,但是每个元素都需要一个指针域,从而产生了结构性开销。
队空条件 : front = rear (初始化时:front = rear ) 队满条件: front = (rear+1) % N (N=maxsize) 队列长度:L=(N+rear-front)% N
线性表、栈与队的异同点
相同点:逻辑结构相同,都是线性的;都可以用顺序存储或链表存储;栈和队列是两种特殊的线性表,即受限的线性表(只是对插入、删除运算加以限制)。
不同点: ① 运算规则不同,线性表为随机存取,插入删除位置随意。而栈是只允许在一端进行插入和删除运算,因而是后进先出表LIFO;队列是只允许在一端进行插入、另一端进行删除运算,因而是先进先出表FIFO。 ② 用途不同,线性表比较通用;堆栈用于函数调用、递归和简化设计等;队列用于离散事件模拟、多道作业处理和简化设计等。