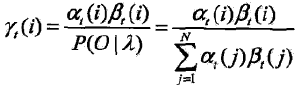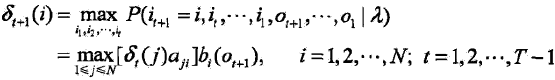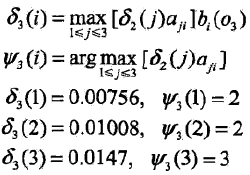隐马尔可夫模型(HMM) - 4 - 预测算法(维特比算法)

声明：

         1，本篇为个人对《2012.李航.统计学习方法.pdf》的学习总结，不得用作商用，欢迎转载，但请注明出处（即：本帖地址）。

         2，由于本人在学习初始时有很多数学知识都已忘记，所以为了弄懂其中的内容查阅了很多资料，所以里面应该会有引用其他帖子的小部分内容，如果原作者看到可以私信我，我会将您的帖子的地址付到下面。

         3，如果有内容错误或不准确欢迎大家指正。

         4，如果能帮到你，那真是太好了。

 

         这里介绍隐马尔可夫模型预测的两种算法：近似算法与维特比算法。

近似算法

         近似算法的想法是：在每个时刻t选择在该时刻最有可能出现的状态i_t^*，从而得到一个状态序列I* = (i₁^*,i₂^*, ..., i_T^*)，将它作为预测的结果。

         给定隐马尔可夫模型λ和观测序列O，在时刻t处于状态q_i的概率γ_t(i)是

                  

         在每一时刻t最有可能的状态i_t^*是

                  

         从而得到状态序列I* =(i₁^*, i₂^*, ..., i_T^*)。

         近似算法的有点是计算简单，其缺点是不能保证预测的状态序列整体是最有可能的状态序列，因为预测的状态序列可能有实际不发生的部分。

         事实上，上述方法得到的状态序列中有可能存在转移概率为0的相邻状态，即，对某些i, j，a_ij=0。

         尽管如此，近似算法仍然是有用的。

维特比算法

         维特比算法实际上用动态规划隐马尔可夫模型预测问题，即，用动态规划(dunamic programming)求概率最大路径(最优路径)。这时一条路径对应着一个状态序列。

         根据动态规划原来，最优路径具有这样的特征：如果最优路径在时刻t通过节点i_t^*，那么这一路径中“从节点i₁^*到终点i_t^*的部分路径”对于“从节点i₁^*到终点i_t^*的所有可能的部分路径”来说必须是最优的。

         根据这一原理，我们只需从时刻t=1开始，递推的计算在时刻t状态为i的各条部分路径的最大概率，直至得到时刻t=T时状态为i的各条路径的最大概率。时刻t=T的最大概率即为最优路径的概率P*，最优路径的终点i_t^*也就同时得到了。

         之后，为了找出最优路径的各个节点，从终结点i_T^*开始，由后向前逐步求得节点i_T-1^*,..., i₁^*，得到最优路径I* = (i₁^*, i₂^*, ..., i_T^*)。

         这就是维特比算法。

         首先导入两个变量δ和ψ。定义在时刻t状态为i的所有单个路径(i₁, i₂, ..., i_t)中概率最大值为：

                  

         由定义可得变量δ的递推公式：

                  

         定义在时刻t状态为i的所有单个路径(i₁,i₂, ... , i_t-1, i_t)中概率最大的路径的第t-1个节点为

                  

         于是维特比算法如下。

 算法(维特比算法)：

                   输入：模型λ= (A, B,π)和观测O=(o₁,o₂, ..., o_T)；

                   输出：最优路径I* = (i₁^*,i₂^*, ..., i_T^*)。

                   过程：

                           

 例子

         考虑盒子和球模型λ=(A, B,π)，状态集合Q={1, 2, 3}，观测集合V={红, 白}，

                  

         已知观测序列O=(红，白，红)，试求最优状态序列，即最优路径I* = (i₁^*, i₂^*, i₃^*)。

         解：

                   如下图所示(图中的数字在之后的步骤中会一一推导出来)

                           

                   要在所有可能的路径中选择一条最优路径，按照以下步骤出来。

                   1，初始化

                   在t=1时，对每个状态i,i=1, 2, 3，求状态为i观测o₁为红的概率，记此概率为δ₁(i)，则：

                            δ₁(i) = π_ib_i(o₁) =π_ib_i(红)， i = 1, 2, 3

                   代入实际数据

                            δ₁(1) = 0.10，δ₁(2) = 0.16，δ₁(3) = 0.28

                   记ψ₁(i) = 0，i = 1, 2, 3。

                   2，在t=n时

                   在t=2时，对每个状态i, i =1,2,3，求在t=1时状态为j观测为红并在t=2时状态为i观测o₂为白的路径的最大概率，记此最大概率为δ₂(i)，则：

                           

                   同时，对每个状态i, i= 1, 2, 3，记录概率最大路径的前一个状态j：

                           

                   计算：

                           

                   同样，在t=3时

                           

                   3，求最优路径的终点

                   以P*表示最优路径的概率，则

                           

                   最优路径的终点是i₃^*:

                           

                   4，逆向找i₂^*,i₁^*：

                            在t=2时，i₂^*= ψ₃(i₃^*) =ψ₃(3) = 3

                            在t=2时，i₁^*= ψ₂(i₂^*) =ψ₂(3) = 3

                   于是求得最优路径，即最有状态序列I* = (i₁^*, i₂^*, i₃^*)= (3, 3, 3)。