[从头学数学] 第211节 带着计算机去高考（三）
剧情提要：
[机器小伟]在[工程师阿伟]的陪同下进入了[九转金丹]之第八转的修炼。设想一个场景：
如果允许你带一台不连网的计算机去参加高考，你会放弃选择一个手拿计算器和草稿本吗
？阿伟决定和小伟来尝试一下用计算机算高考题会是怎样的感觉。
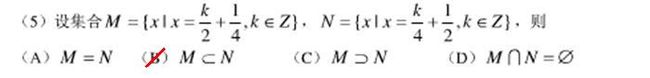
![[从头学数学] 第211节 带着计算机去高考（三）_第5张图片](http://img.e-com-net.com/image/info5/6f4e91122cfb4f45b3eb80e8a13c0fa3.jpg)
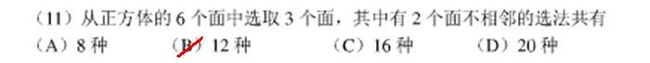
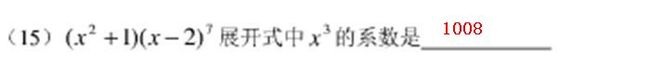
命名有点乱，用的时候要小心，很容易出错的。
下面是上一篇中的几何部分现在可调用的功能：
[机器小伟]在[工程师阿伟]的陪同下进入了[九转金丹]之第八转的修炼。设想一个场景：
如果允许你带一台不连网的计算机去参加高考，你会放弃选择一个手拿计算器和草稿本吗
？阿伟决定和小伟来尝试一下用计算机算高考题会是怎样的感觉。
正剧开始：
星历2016年05月18日 14:57:54, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起做着2002年的江苏省数学高考题]。
![[从头学数学] 第211节 带着计算机去高考（三）_第1张图片](http://img.e-com-net.com/image/info5/a1091816f6ef4f58863459539b0c1519.jpg)
<span style="font-size:18px;">#题1
>>>
0.5000110003630133
def tmp1():
d = geo.plDistance2D([1,0], [[0,0], [1.732, 1]]);
print(d);</span>
![[从头学数学] 第211节 带着计算机去高考（三）_第2张图片](http://img.e-com-net.com/image/info5/de87a7967ade4b68be9c6b7dd7a9fe29.jpg)
<span style="font-size:18px;">#题2
def tmp2():
a = (0.5+0.866j)**3;
print(a);
>>>
(-0.9999339999999999+3.8104000000038774e-05j)</span>
![[从头学数学] 第211节 带着计算机去高考（三）_第3张图片](http://img.e-com-net.com/image/info5/36fb406aed684647aa7d450b039ee10b.jpg)
<span style="font-size:18px;">//题3
if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,180);
//坐标轴设定
var scaleX = 2*r, scaleY = 2*r;
var spaceX = 1, spaceY = 1;
var xS = -10, xE = 10;
var yS = -10, yE = 10;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var transform = new Transform();
//存放函数图像上的点
var a = [], b = [], c = [], d = [];
//需要显示的函数说明
//希腊字母表(存此用于Ctrl C/V
//ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ
//αβγδεζηθικλμνξοπρστυφχψω
var f1 = '(1+x)(1-|x|)', f2 = '', f3 = '', f4 = '';
//(1-(x+2)^2)^0.5
for (var x = xS; x <= xE; x+=0.2) {
a.push([x, taskFun(x)]);
}
//存放临时数组
var tmp = [];
//显示变换
if (a.length > 0) {
a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(a);
shape.pointDraw(tmp, 'red');
tmp = [].concat(a);
shape.multiLineDraw(tmp, 'pink');
plot.setFillStyle('red');
plot.fillText(f1, 100, -90, 200);
}
}
function taskFun(x) {
return (1+x)*(1-Math.abs(x));
}</span>
![[从头学数学] 第211节 带着计算机去高考（三）_第4张图片](http://img.e-com-net.com/image/info5/defbca63274e46b381d8a7379b8c3170.png)
<span style="font-size:18px;">//题4
if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,180);
//坐标轴设定
var scaleX = 2*r, scaleY = 2*r;
var spaceX = 1, spaceY = 1;
var xS = -10, xE = 10;
var yS = -10, yE = 10;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var transform = new Transform();
//存放函数图像上的点
var a = [], b = [], c = [], d = [];
//需要显示的函数说明
//希腊字母表(存此用于Ctrl C/V
//ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ
//αβγδεζηθικλμνξοπρστυφχψω
var f1 = 'sinx-cosx', f2 = '', f3 = '', f4 = '';
//(1-(x+2)^2)^0.5
for (var x = 0; x <= Math.PI*2; x+=0.2) {
a.push([x, taskFun(x)]);
}
//存放临时数组
var tmp = [];
//显示变换
if (a.length > 0) {
a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(a);
shape.pointDraw(tmp, 'red');
tmp = [].concat(a);
shape.multiLineDraw(tmp, 'pink');
plot.setFillStyle('red');
plot.fillText(f1, 100, -90, 200);
}
}
}
function taskFun(x) {
return Math.sin(x) - Math.cos(x);
}</span>
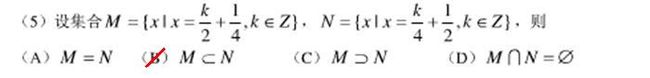
<span style="font-size:18px;">#题5
def tmp5():
M = [];
N = [];
for i in range(-10, 10, 1):
M.append(i/2+1/4);
N.append(i/4+1/2);
print('M=', M);
print('N=', N);
setM = set(M);
setN = set(N);
print(setM.intersection(setN));
>>>
M= [-4.75, -4.25, -3.75, -3.25, -2.75, -2.25, -1.75, -1.25, -0.75, -0.25, 0.25, 0.75, 1.25, 1.75, 2.25, 2.75, 3.25, 3.75, 4.25, 4.75]
N= [-2.0, -1.75, -1.5, -1.25, -1.0, -0.75, -0.5, -0.25, 0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5, 2.75]
{-0.75, -0.25, 2.75, 1.75, 0.25, 1.25, 2.25, -1.25, 0.75, -1.75}
</span>
![[从头学数学] 第211节 带着计算机去高考（三）_第6张图片](http://img.e-com-net.com/image/info5/f7898ed177754b8594fdb8ffd684c8df.png)
<span style="font-size:18px;">//题6
if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,180);
//坐标轴设定
var scaleX = 2*r, scaleY = 2*r;
var spaceX = 2, spaceY = 2;
var xS = -10, xE = 10;
var yS = -10, yE = 10;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var transform = new Transform();
//存放函数图像上的点
var a = [], b = [], c = [], d = [];
//需要显示的函数说明
//希腊字母表(存此用于Ctrl C/V
//ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ
//αβγδεζηθικλμνξοπρστυφχψω
var f1 = 'x=t^[2], y=2t', f2 = '', f3 = '', f4 = '';
//(1-(x+2)^2)^0.5
for (var x = xS; x <= xE; x+=0.2) {
a.push([x*x, 2*x]);
}
//存放临时数组
var tmp = [];
//显示变换
if (a.length > 0) {
a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(a);
shape.pointDraw(tmp, 'red');
tmp = [].concat(a);
shape.multiLineDraw(tmp, 'pink');
plot.setFillStyle('red');
plot.fillText(f1, 100, -180, 200);
}
} </span>
<span style="font-size:18px;">#题7
def tmp7():
s = ['2/3pr^[3]','1/3pr^[2]h'];
#h = 2r
thita = 2*math.atan(0.5);
print(math.cos(thita));
>>>
0.6000000000000001</span>
![[从头学数学] 第211节 带着计算机去高考（三）_第7张图片](http://img.e-com-net.com/image/info5/94ec7312414b40159a4a036bdcdbdba8.jpg)
![[从头学数学] 第211节 带着计算机去高考（三）_第8张图片](http://img.e-com-net.com/image/info5/b8b93027d9624662842553b2c6cc1c9e.png)
<span style="font-size:18px;">//题10
if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,180);
//坐标轴设定
var scaleX = 2*r, scaleY = 2*r;
var spaceX = 2, spaceY = 2;
var xS = -10, xE = 10;
var yS = -10, yE = 10;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var transform = new Transform();
//存放函数图像上的点
var a = [], b = [], c = [], d = [];
//需要显示的函数说明
//希腊字母表(存此用于Ctrl C/V
//ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ
//αβγδεζηθικλμνξοπρστυφχψω
var f1 = 'y = 1 - 1/(x-1)', f2 = '', f3 = '', f4 = '';
var y = 0;
//(1-(x+2)^2)^0.5
for (var x = xS; x <= xE; x+=0.2) {
y = taskFun(x);
if (y != Number.NaN) {
a.push([x, y]);
}
}
//存放临时数组
var tmp = [];
//显示变换
if (a.length > 0) {
a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(a);
shape.pointDraw(tmp, 'red');
tmp = [].concat(a);
shape.multiLineDraw(tmp, 'pink');
plot.setFillStyle('red');
plot.fillText(f1, 100, -180, 200);
}
}
}
function taskFun(x) {
return 1- 1/(x-1);
}
</span>
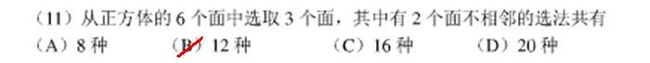
<span style="font-size:18px;">#题11
def tmp11():
#从正方体中选两个相对的面
step1 = 3;
#每组对面有各个中间面
step2 = 4;
result = step1 * step2;
print(result);
>>>
12</span>
<span style="font-size:18px;">#题12
def tmp12():
print(95993*(1.073)**4);
>>>
127244.3338498723</span>
![[从头学数学] 第211节 带着计算机去高考（三）_第9张图片](http://img.e-com-net.com/image/info5/d3d6b3adaad24433980cfb5efa868d79.png)
<span style="font-size:18px;">#题14
def tmp14():
#5/k-1 = 4 =>k =1</span>
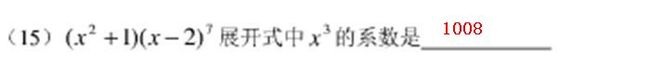
<span style="font-size:18px;">#题15
def tmp15():
a = ['x^[2]', '1'];
b = ['x', '-2'];
a = strformat(a);
b = strformat(b);
#乘方7次
c = strpow_n(b, 7);
#整理
d = strcombine(c);
#多项式乘法一次
e = strdot(a, d);
#整理
f = strcombine(e);
print(f);
>>>
['(1)*x^[9]', '(-14)*x^[8]', '(85)*x^[7]', '(-294)*x^[6]', '(644)*x^[5]', '(-952)*x^[4]', '(1008)*x^[3]', '(-800)*x^[2]', '(448)*x^[1]', '(-128)']
</span>
<span style="font-size:18px;">#题16
def tmp16():
a = [1, 2, 1/2, 3, 1/3, 4, 1/4];
sum_ = 0;
for i in range(len(a)):
sum_ += f(a[i]);
print(sum_);
def f(x):
return x**2/(1+x**2);
</span>
![[从头学数学] 第211节 带着计算机去高考（三）_第10张图片](http://img.e-com-net.com/image/info5/35fe7339e5e34d09ad105475fb27ab7f.jpg)
<span style="font-size:18px;">#题20
def tmp20():
#a_[1] = 30;
#a_[n] = a_[n-1]*0.94+x
q = alg.strformat(['0.94']);
x = alg.strformat(['x']);
a_1 = alg.strformat(['30']);
a_2 = alg.stradd(alg.strdot(q, a_1), x);
a_2 = alg.strcombine(a_2);
for i in range(25):
a_2 = alg.stradd(alg.strdot(q, a_2), x);
a_2 = alg.strcombine(a_2);
print(a_2);
#13x+6<60 x<3
#x 是以1为首项, 0.94为公比的等比数列的前N项和
Sx = 1/0.06 = 16;
#x < 60/16
#这是25年的数据
>>>
['(26.508)', '(1.94)*x^[1]']
['(24.91752)', '(2.8236)*x^[1]']
['(23.422469)', '(3.654184)*x^[1]']
['(22.017121)', '(4.434933)*x^[1]']
['(20.696094)', '(5.168837)*x^[1]']
['(19.454328)', '(5.858707)*x^[1]']
['(18.287068)', '(6.507185)*x^[1]']
['(17.189844)', '(7.116754)*x^[1]']
['(16.158453)', '(7.689749)*x^[1]']
['(15.188946)', '(8.228364)*x^[1]']
['(14.277609)', '(8.734662)*x^[1]']
['(13.420952)', '(9.210582)*x^[1]']
['(12.615695)', '(9.657947)*x^[1]']
['(11.858753)', '(10.07847)*x^[1]']
['(11.147228)', '(10.473762)*x^[1]']
['(10.478394)', '(10.845336)*x^[1]']
['(9.84969)', '(11.194616)*x^[1]']
['(9.258709)', '(11.522939)*x^[1]']
['(8.703186)', '(11.831563)*x^[1]']
['(8.180995)', '(12.121669)*x^[1]']
['(7.690135)', '(12.394369)*x^[1]']
['(7.228727)', '(12.650707)*x^[1]']
['(6.795003)', '(12.891665)*x^[1]']
['(6.387303)', '(13.118165)*x^[1]']
['(6.004065)', '(13.331075)*x^[1]']
</span>
<span style="font-size:18px;">//题21
if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,180);
//坐标轴设定
var scaleX = 2*r, scaleY = 2*r;
var spaceX = 2, spaceY = 2;
var xS = -10, xE = 10;
var yS = -10, yE = 10;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var transform = new Transform();
//存放函数图像上的点
var a = [], b = [], c = [], d = [];
//需要显示的函数说明
//希腊字母表(存此用于Ctrl C/V
//ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ
//αβγδεζηθικλμνξοπρστυφχψω
var f1 = 'y = x^2+|x-2|+1', f2 = 'y = x^2+|x+2|+1', f3 = '', f4 = '';
var y1 = y2 = 0;
//(1-(x+2)^2)^0.5
for (var x = xS; x <= xE; x+=0.2) {
y1 = x*x+Math.abs(x-2)+1;
y2 = x*x+Math.abs(x+2)+1;
if (y1 != Number.NaN) {
a.push([x, y1]);
}
if (y2 != Number.NaN) {
b.push([x, y2]);
}
}
//存放临时数组
var tmp = [];
//显示变换
if (a.length > 0) {
a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(a);
shape.pointDraw(tmp, 'red');
tmp = [].concat(a);
shape.multiLineDraw(tmp, 'pink');
plot.setFillStyle('red');
plot.fillText(f1, 100, -90, 200);
}
if (b.length > 0) {
b = transform.scale(transform.translate(b, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(b);
shape.pointDraw(tmp, 'blue');
tmp = [].concat(b);
shape.multiLineDraw(tmp, 'blue');
plot.setFillStyle('blue');
plot.fillText(f2, 100, -120, 200);
}
} </span>
好了，这次题就做到这里，这张试卷的难度比前两年的要低上2环。
先说明一下这个环的意思：
你找到一把钥匙，开了一个宝箱，然后拿走宝物，这叫一环难度；
这把钥匙开了一个宝箱，里面没有宝物，只有另一把钥匙，
你再找一个宝箱开了，宝物在里面，你拿到手，这叫二环难度；
以此类推啦，这张试卷的最难的题也就四环难度，前两年的达到六环。
一般两环难度以下是送分题，大概30到40分，三环难度的再给30分。
四环难度要是给个50分，这张卷子就已经比较厚道了。然后是五环难度，
一般出到六环难度就是伤天害理的感觉了。
前两年的卷子大致是：二环20分，三环20分，四环40分，五环40分，然后是六环，
然后陷阱还多，明明一个四环题，伪装成两环的，特别阴险，这就是江苏卷的特色。
这张是很温和的啦，运算量也不大。
这次[工程师阿伟]终于把早就想做的那个代数式运算工具搞出来了，这可是很好玩的一个东西。
<span style="font-size:18px;">###
# @usage 代数式字符串的运算
# @author mw
# @date 2016年05月17日 星期二 16:48:56
# @param
# @return
#
###
#计算代数式用, 传入的是单项式，返回coef*expr的形式
def strmono(s):
#'x', '-x', '2x', '-2x', '-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]'
stmp = s;
size = len(stmp);
alphaIndex = 0;
signIndex = 0;
for i in range(size):
if (stmp[i].isalpha()):
alphaIndex = i;
break;
if (i >= size-1):
alphaIndex = i+1;
if (stmp[0] == '-'):
signIndex = 1;
if (signIndex >= alphaIndex):
return monoformat('(-1)*'+stmp[alphaIndex:]);
else:
if alphaIndex >= size:
return monoformat('(-'+stmp[signIndex:alphaIndex]+')');
return monoformat('(-'+stmp[signIndex:alphaIndex]+')*'+stmp[alphaIndex:]);
else:
signIndex = 0;
if (signIndex >= alphaIndex):
return monoformat('(1)*'+stmp[alphaIndex:]);
else:
if alphaIndex >= size:
return monoformat('('+stmp[signIndex:alphaIndex]+')');
return monoformat('('+stmp[signIndex:alphaIndex]+')*'+stmp[alphaIndex:]);
#计算两个单项式的乘积
def strmul(mono1, mono2):
#这个处理是保证每个单项式统一格式(coef)*expr
'''
if (mono1[0] != '(' or mono2[0] != '('):
#如果没有规格化，那么就做一下
mono1 = strmono(mono1);
mono2 = strmono(mono2);
'''
stmp1 = mono1;
stmp2 = mono2;
#乘号的位置
signIndex1 = stmp1.find('*');
signIndex2 = stmp2.find('*');
if (signIndex1 == -1):
coef1 = stmp1;
expr1 = '';
else:
coef1 = stmp1[:signIndex1];
expr1 = stmp1[signIndex1+1:];
if (signIndex2 == -1):
coef2 = stmp2;
expr2 = '';
else:
coef2 = stmp2[:signIndex2];
expr2 = stmp2[signIndex2+1:];
coef = coef1+'*'+coef2;
if (signIndex1 == -1 or signIndex2 == -1):
expr = expr1+expr2;
else:
expr = expr1+'*'+expr2;
if (expr == ''):
return '('+str(round(eval(coef), 6))+')';
return '('+str(round(eval(coef), 6))+')*'+expr;
#计算两个单项式的商
def strdiv(s1, s2):
#这个处理是保证每个单项式统一格式(coef)*expr
stmp1 = strmono(s1);
stmp2 = strmono(s2);
#乘号的位置
signIndex1 = stmp1.find('*');
signIndex2 = stmp2.find('*');
if (signIndex1 == -1):
coef1 = stmp1;
expr1 = '';
else:
coef1 = stmp1[:signIndex1];
expr1 = stmp1[signIndex1+1:];
if (signIndex2 == -1):
coef2 = stmp2;
expr2 = '';
else:
coef2 = stmp2[:signIndex2];
expr2 = stmp2[signIndex2+1:];
coef = coef1+'/'+coef2;
if (signIndex1 == -1 and signIndex2 != -1):
expr = '('+expr2+')^[-1]';
elif (signIndex1 == -1 or signIndex2 == -1):
expr = expr1+expr2;
else:
expr = expr1+'/'+expr2;
if (expr == ''):
return '('+str(round(eval(coef), 6))+')';
return '('+str(round(eval(coef), 6))+')*'+expr;
#找一个字符串中所有待查找子串的位置，返回位置阵列
def findall(string, sub):
size = len(string);
index = [];
cur = string.find(sub);
index.append(cur)
while (index[-1] != -1):
cur = string.find(sub, index[-1]+1);
index.append(cur);
return index;
#计算单项式的乘方, s^n
def strpow(s, n):
stmp = strmono(s);
signIndex = stmp.find('*');
if (signIndex == -1):
coef = stmp+'**'+str(n);
expr = '';
return '('+str(round(eval(coef), 6))+')';
else:
coef = stmp[:signIndex]+'**'+str(n);
expr = '('+stmp[signIndex+1:]+')^['+str(n)+']';
return '('+str(round(eval(coef), 6))+')*'+expr;
#计算代数式用，传入的两个阵列都具有['s1', 's2', ..., 'sn']这样的格式
def strdot(array1, array2):
size1 = len(array1);
size2 = len(array2);
result = [];
for i in range(size1):
for j in range(size2):
result.append(strmul(array1[i], array2[j]));
return result;
#把格式化后的单项式分解成[coef, expr]对组的形式
def explodemono(mono):
stmp = mono;
#乘号的位置
signIndex = stmp.find('*');
if (signIndex == -1):
coef = stmp;
expr = '';
else:
coef = stmp[:signIndex];
expr = stmp[signIndex+1:];
return [coef, expr];
#合并同类项，传入的阵列具有['s1', 's2', ..., 'sn']这样的格式
def strcombine(array):
size = len(array);
explode = [];
for i in range(size):
#这里传入的阵列已经是规格化后的了，否则要加一层strmono处理。
explode.append(explodemono(monocombine(array[i])));
result = [];
for i in range(size):
size_1 = len(result);
if size_1 <= 0:
result.append(explode[i]);
else:
for j in range(size_1):
if result[j][1] == explode[i][1]:
result[j][0] = result[j][0] + '+' + explode[i][0];
break;
if j >= size_1-1:
result.append(explode[i]);
result_1 = [];
size_1 = len(result);
for j in range(size_1):
result[j][0] = str(round(eval(result[j][0]), 6));
if (result[j][0] == '0'):
result_1.append('(0)');
else:
tmps = result[j][1];
if (tmps == ''):
result_1.append('('+result[j][0]+')');
else:
result_1.append('('+result[j][0]+')*'+result[j][1]);
return result_1;
#指数为正整数的乘方
def strpow_n(array, n):
#计算
result = [];
if (n == 1):
result = array;
elif (n == 2):
result = strdot(array, array);
elif (n >= 3):
tmp = strdot(array, array);
n -= 2;
while (n > 0):
result = strdot(tmp, array);
tmp = result;
n -= 1;
return result;
#阵列取负
def minus(array):
for i in range(len(array)):
if array[i][1] == '-':
#array[i][0]是'(, 这是规范
array[i] = array[i][0]+array[i][2:];
else:
array[i] = array[i][0]+'-'+array[i][1:];
return array;
###
# @usage 代数式运算
# @author mw
# @date 2016年05月18日 星期三 07:37:01
# @param
# @return
#
###
#两个多项式相加，合并同类项不在此进行
def stradd(array1, array2):
#两个多项式相加，这里直接返回数组的相加
return array1+array2;
#为了简便输入，不要求输入规范化代数式，(coef)*expr形式
#所以在此对多项式进行规范化
#至于单项式规范化，调用strmono函数即可
def strformat(array):
for i in range(len(array)):
array[i] = strmono(array[i]);
return array;
#把单项式完全格式化，使经过运算的没运算过的都具有统一的格式
def monoformat(mono):
#规范化单项式，保证任意两个参数之间都添加一个'*'号
#这是为了和经过代数式乘法运算之后的格式统一
chars = len(mono);
s = '';
for i in range(chars-1):
if mono[i] == ']' and mono[i+1].isalpha():
s += mono[i]+'*';
elif mono[i].isalpha() and mono[i+1].isalpha():
s += mono[i]+'*';
#这里还有一个死角，就是下标或指数如果是用的代数式，并且是多项相乘
#可能会有一点问题，暂时不考虑了
else:
s += mono[i];
s += mono[-1];
return s;
#把单项式炸开，这里的单项式已经达到最大规范化，是(coef)*x_[1]^[2]*y_[2]^[2]这种结构形式了
#'*'号是要作为分隔符的，不可缺少
def explodemono_2(mono):
part = mono.split('*');
#每个部分的[前部，指数部]的对组
map_ = [];
for i in range(len(part)):
expIndex = part[i].find('^');
if (expIndex != -1):
map_.append([part[i][:expIndex], part[i][expIndex:]]);
else:
s = part[i];
#系数
if s[0] == '(':
map_.append([part[i], '']);
#代数式
else:
map_.append([part[i], '^[1]']);
map_ = sorted(map_, key = lambda a : a[0]);
return map_;
#单项式同类项合并
def monocombine(mono):
map_ = explodemono_2(mono);
size = len(map_);
result = [];
for i in range(size):
size_1 = len(result);
if (size_1 <= 0):
result.append(map_[i]);
else:
for j in range(size_1):
if result[j][0] == map_[i][0]:
#双方的中括号位置
#由于规范化后的原因，这个括号是一定有的
p1 = result[j][1].find('[');
p2 = result[j][1].find(']');
p3 = map_[i][1].find('[');
p4 = map_[i][1].find(']');
s = result[j][1][p1+1:p2]+'+'+map_[i][1][p3+1:p4];
size_2 = len(s);
for k in range(size_2):
if s[k].isalpha():
break;
#如果没有字符参数，可以计算出结果，就计算
if (k >= size_2-1):
s = str(eval(s));
result[j][1] = '^['+s+']';
break;
if (j >= size_1-1):
result.append(map_[i]);
size_1 = len(result);
s = '';
for i in range(size_1):
if (i > 0 and result[i][1] == '^[0]'):
continue;
s += result[i][0]+result[i][1];
if (i < size_1-1):
s += '*';
return s;
#排列公式
def arrangement(n, m):
if n < m:
return arrangement(m, n);
else:
factorial = 1;
for i in range(n, n-m, -1):
factorial*=i;
return factorial;
#组合公式
def combination(n, m):
if (n < m):
return combination(m, n);
else:
return arrangement(n, m)/arrangement(m,m);
'''
if __name__ == '__main__':
a = ['x^[2]', '1'];
b = ['x', '-2'];
a = strformat(a);
b = strformat(b);
#乘方7次
c = strpow_n(b, 7);
#整理
d = strcombine(c);
#多项式乘法一次
e = strdot(a, d);
#整理
f = strcombine(e);
print(f);
>>>
['(1)*x^[9]', '(-14)*x^[8]', '(85)*x^[7]', '(-294)*x^[6]', '(644)*x^[5]', '(-952)*x^[4]',
'(1008)*x^[3]', '(-800)*x^[2]', '(448)*x^[1]', '(-128)']
'''</span>
命名有点乱，用的时候要小心，很容易出错的。
再给出一些用例和过程作为参考：
<span style="font-size:18px;">def tmp():
s = ['-3', '3', 'x', '-x', '2x', '-2x', '-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]'];
for i in range(len(s)):
print(strmono(s[i]));
>>>
['(1)*x^[2]*x^[2]', '(-1)*x^[2]*y', '(-1)*y*x^[2]', '(1)*y*y']
#两个多项式相加，合并同类项不在此进行
def stradd(array1, array2):
#两个多项式相加，这里直接返回数组的相加
return array1+array2;
#为了简便输入，不要求输入规范化代数式，(coef)*expr形式
#所以在此对多项式进行规范化
#至于单项式规范化，调用strmono函数即可
def strformat(array):
for i in range(len(array)):
array[i] = strmono(array[i]);
return array;
def tmp():
A = ['x^[2]', '-y'];
B = strdot(A, A);
print(B);
>>>
['(1)*x^[2]*x^[2]', '(-1)*x^[2]*y', '(-1)*y*x^[2]', '(1)*y*y']
['(1)*x^[2]', '(-1)*y']
['((1)*)*x^[2]', '((-1)*)*y']
def tmp():
A = ['x^[2]', '-y'];
B = strdot(A, A);
print(B);
C = strformat(A);
print(C);
#规范化只能进行一次，否则会解析出无法计算的表达式
D = strformat(C);
print(D);
>>>
['(-3)', '(3)', '(1)*x', '(-1)*x', '(2)*x', '(-2)*x', '(-2)*x^[2]', '(3)*x_[2]^[3]', '(-3)*x_[2]^[3]', '(-2)*x^[3]y^[3]', '(3)*x^[-1]y^[2]']
def tmp():
s = ['-3', '3', 'x', '-x', '2x', '-2x',
'-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]',
'-2x^[3]y^[3]', '3x^[-1]y^[2]'];
s1 = strformat(s);
print(s1);
>>>
['(-3)', '(3)', '(1)*x', '(-1)*x', '(2)*x', '(-2)*x', '(-2)*x^[2]', '(3)*x_[2]^[3]', '(-3)*x_[2]^[3]', '(-2)*x^[3]y^[3]', '(3)*x^[-1]y^[2]']
['(-3)', '(3)', '(1)*x', '(-1)*x', '(2)*x', '(-2)*x', '(-2)*x^[2]', '(3)*x_[2]^[3]', '(-3)*x_[2]^[3]', '(-2)*x^[3]*y^[3]', '(3)*x^[-1]*y^[2]']
def tmp():
s = ['-3', '3', 'x', '-x', '2x', '-2x',
'-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]',
'-2x^[3]y^[3]', '3x^[-1]y^[2]'];
s1 = strformat(s);
print(s1);
for i in range(len(s1)):
s1[i] = monoformat(s1[i]);
print(s1);
#把单项式完全格式化，使经过运算的没运算过的都具有统一的格式
def monoformat(mono):
#规范化单项式，保证任意两个参数之间都添加一个'*'号
#这是为了和经过代数式乘法运算之后的格式统一
chars = len(mono);
s = '';
for i in range(chars-1):
if mono[i] == ']' and mono[i+1].isalpha():
s += mono[i]+'*';
elif mono[i].isalpha() and mono[i+1].isalpha():
s += mono[i]+'*';
#这里还有一个死角，就是下标或指数如果是用的代数式，并且是多项相乘
#可能会有一点问题，暂时不考虑了
else:
s += mono[i];
s += mono[-1];
return s;
>>>
['(-3)', '(3)', '(1)*x', '(-1)*x', '(2)*x', '(-2)*x', '(-2)*x^[2]', '(3)*x_[2]^[3]', '(-3)*x_[2]^[3]', '(-2)*x^[3]*y^[3]', '(3)*y^[2]*x^[-1]', '(5)*x*y*x']
[['(-3)', '']]
[['(3)', '']]
[['(1)', ''], ['x', '']]
[['(-1)', ''], ['x', '']]
[['(2)', ''], ['x', '']]
[['(-2)', ''], ['x', '']]
[['(-2)', ''], ['x', '^[2]']]
[['(3)', ''], ['x_[2]', '^[3]']]
[['(-3)', ''], ['x_[2]', '^[3]']]
[['(-2)', ''], ['x', '^[3]'], ['y', '^[3]']]
[['(3)', ''], ['x', '^[-1]'], ['y', '^[2]']]
[['(5)', ''], ['x', ''], ['x', ''], ['y', '']]
#把单项式炸开，这里的单项式已经达到最大规范化，是(coef)*x_[1]^[2]*y_[2]^[2]这种结构形式了
#'*'号是要作为分隔符的，不可缺少
def explodemono_2(mono):
part = mono.split('*');
#每个部分的[前部，指数部]的对组
map_ = [];
for i in range(len(part)):
expIndex = part[i].find('^');
if (expIndex != -1):
map_.append([part[i][:expIndex], part[i][expIndex:]]);
else:
map_.append([part[i], '']);
map_ = sorted(map_, key = lambda a : a[0]);
return map_;
def tmp():
s = ['-3', '3', 'x', '-x', '2x', '-2x',
'-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]',
'-2x^[3]y^[3]', '3y^[2]x^[-1]', '5xyx'];
s1 = strformat(s);
print(s1);
for i in range(len(s1)):
print(explodemono_2(s1[i]));
>>>
['(-3)', '(3)', '(1)*x', '(-1)*x', '(2)*x', '(-2)*x', '(-2)*x^[2]', '(3)*x_[2]^[3]', '(-3)*x_[2]^[3]', '(-2)*x^[3]*y^[3]', '(3)*y^[2]*x^[-1]', '(5)*x*y*x']
[['(-3)', '']]
[['(3)', '']]
[['(1)', ''], ['x', '^[1]']]
[['(-1)', ''], ['x', '^[1]']]
[['(2)', ''], ['x', '^[1]']]
[['(-2)', ''], ['x', '^[1]']]
[['(-2)', ''], ['x', '^[2]']]
[['(3)', ''], ['x_[2]', '^[3]']]
[['(-3)', ''], ['x_[2]', '^[3]']]
[['(-2)', ''], ['x', '^[3]'], ['y', '^[3]']]
[['(3)', ''], ['x', '^[-1]'], ['y', '^[2]']]
[['(5)', ''], ['x', '^[1]'], ['x', '^[1]'], ['y', '^[1]']]
#把单项式炸开，这里的单项式已经达到最大规范化，是(coef)*x_[1]^[2]*y_[2]^[2]这种结构形式了
#'*'号是要作为分隔符的，不可缺少
def explodemono_2(mono):
part = mono.split('*');
#每个部分的[前部，指数部]的对组
map_ = [];
for i in range(len(part)):
expIndex = part[i].find('^');
if (expIndex != -1):
map_.append([part[i][:expIndex], part[i][expIndex:]]);
else:
s = part[i];
#系数
if s[0] == '(':
map_.append([part[i], '']);
#代数式
else:
map_.append([part[i], '^[1]']);
map_ = sorted(map_, key = lambda a : a[0]);
return map_;
def tmp():
s = ['-3', '3', 'x', '-x', '2x', '-2x',
'-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]',
'-2x^[3]y^[3]', '3y^[2]x^[-1]', '5xyx'];
s1 = strformat(s);
print(s1);
for i in range(len(s1)):
print(explodemono_2(s1[i]));
>>>
['(-3)', '(3)', '(1)*x', '(-1)*x', '(2)*x', '(-2)*x', '(-2)*x^[2]', '(3)*x_[2]^[3]', '(-3)*x_[2]^[3]', '(-2)*x^[3]*y^[3]', '(3)*y^[2]*x^[-1]', '(5)*x*y*x']
[['(-3)', '']]
[['(3)', '']]
[['(1)', ''], ['x', '^[1]']]
[['(-1)', ''], ['x', '^[1]']]
[['(2)', ''], ['x', '^[1]']]
[['(-2)', ''], ['x', '^[1]']]
[['(-2)', ''], ['x', '^[2]']]
[['(3)', ''], ['x_[2]', '^[3]']]
[['(-3)', ''], ['x_[2]', '^[3]']]
[['(-2)', ''], ['x', '^[3]'], ['y', '^[3]']]
[['(3)', ''], ['x', '^[-1]'], ['y', '^[2]']]
[['(5)', ''], ['x', '^[1+1]'], ['y', '^[1]']]
#单项式同类项合并
def monocombine(mono):
map_ = explodemono_2(mono);
size = len(map_);
result = [];
for i in range(size):
size_1 = len(result);
if (size_1 <= 0):
result.append(map_[i]);
else:
for j in range(size_1):
if result[j][0] == map_[i][0]:
#双方的中括号位置
#由于规范化后的原因，这个括号是一定有的
p1 = result[j][1].find('[');
p2 = result[j][1].find(']');
p3 = map_[i][1].find('[');
p4 = map_[i][1].find(']');
s = result[j][1][p1+1:p2]+'+'+map_[i][1][p3+1:p4];
result[j][1] = '^['+s+']';
break;
if (j >= size_1-1):
result.append(map_[i]);
return result;
def tmp():
s = ['-3', '3', 'x', '-x', '2x', '-2x',
'-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]',
'-2x^[3]y^[3]', '3y^[2]x^[-1]', '5xyx'];
s1 = strformat(s);
print(s1);
for i in range(len(s1)):
print(monocombine(s1[i]));
>>>
['(-3)', '(3)', '(1)*x', '(-1)*x', '(2)*x', '(-2)*x', '(-2)*x^[2]', '(3)*x_[2]^[3]', '(-3)*x_[2]^[3]', '(-2)*x^[3]*y^[3]', '(3)*y^[2]*x^[-1]', '(5)*x*y*x^[2]*z*y*x*x_[1]']
(-3)
(3)
(1)*x^[1]
(-1)*x^[1]
(2)*x^[1]
(-2)*x^[1]
(-2)*x^[2]
(3)*x_[2]^[3]
(-3)*x_[2]^[3]
(-2)*x^[3]*y^[3]
(3)*x^[-1]*y^[2]
(5)*x^[1+2+1]*x_[1]^[1]*y^[1+1]*z^[1]
#单项式同类项合并
def monocombine(mono):
map_ = explodemono_2(mono);
size = len(map_);
result = [];
for i in range(size):
size_1 = len(result);
if (size_1 <= 0):
result.append(map_[i]);
else:
for j in range(size_1):
if result[j][0] == map_[i][0]:
#双方的中括号位置
#由于规范化后的原因，这个括号是一定有的
p1 = result[j][1].find('[');
p2 = result[j][1].find(']');
p3 = map_[i][1].find('[');
p4 = map_[i][1].find(']');
s = result[j][1][p1+1:p2]+'+'+map_[i][1][p3+1:p4];
result[j][1] = '^['+s+']';
break;
if (j >= size_1-1):
result.append(map_[i]);
size_1 = len(result);
s = '';
for i in range(size_1):
s += result[i][0]+result[i][1];
if (i < size_1-1):
s += '*';
return s;
def tmp():
s = ['-3', '3', 'x', '-x', '2x', '-2x',
'-2x^[2]', '3x_[2]^[3]', '-3x_[2]^[3]',
'-2x^[3]y^[3]', '3y^[2]x^[-1]', '5xyx^[2]zyxx_[1]'];
s1 = strformat(s);
print(s1);
for i in range(len(s1)):
print(monocombine(s1[i]));
>>>
['(1)*x*x', '(1)*x*y', '(1)*x*z', '(1)*y*x', '(1)*y*y', '(1)*y*z', '(1)*z*x', '(1)*z*y', '(1)*z*z']
def tmp():
A = ['x', 'y', 'z'];
B = ['x', 'y', 'z'];
A = strformat(A);
B = strformat(B);
C = strdot(A, B);
print(C);
>>>
['(1)*x*x', '(1)*x*y', '(1)*x*z', '(1)*y*x', '(1)*y*y', '(1)*y*z', '(1)*z*x', '(1)*z*y', '(1)*z*z']
['(1)*x^[1+1]', '(2)*x^[1]*y^[1]', '(2)*x^[1]*z^[1]', '(1)*y^[1+1]', '(2)*y^[1]*z^[1]', '(1)*z^[1+1]']
def tmp():
A = ['x', 'y', 'z'];
B = ['x', 'y', 'z'];
A = strformat(A);
B = strformat(B);
C = strdot(A, B);
print(C);
C = strcombine(C);
print(C);
['(3)*x', '(3)*y', '(1)*y*x', '(1)*y*y', '(1)*z*x', '(1)*z*y']
['(3)*x^[1]', '(3)*y^[1]', '(1)*x^[1]*y^[1]', '(1)*y^[1+1]', '(1)*x^[1]*z^[1]', '(1)*y^[1]*z^[1]']
def tmp():
A = ['3', 'y', 'z'];
B = ['x', 'y'];
A = strformat(A);
B = strformat(B);
C = strdot(A, B);
print(C);
C = strcombine(C);
print(C);
</span>
下面是上一篇中的几何部分现在可调用的功能：
<span style="font-size:18px;">>>> import geo;
>>> dir(geo);
['__builtins__', '__cached__', '__doc__', '__file__', '__initializing__', '__loader__', '__name__', '__package__', 'angleBetweenTwoLine', 'angleFromX', 'circle', 'crossPointOfTwoLine', 'distance2D', 'interceptOfLine', 'lcCrossPoint2D', 'lcDistance2D', 'lineDistance2D', 'math', 'parallelCheck', 'perpendicular', 'plDistance2D', 'pointFromCircle', 'pointInLine', 'slope', 'tangencyPoint']
>>> help(geo);
Help on module geo:
NAME
geo
FUNCTIONS
angleBetweenTwoLine(Line_1, Line_2)
#两直线夹角 Line_1:[Point_1, Point_2], Line_2:[Point_1, Point_2]
angleFromX(Point_1, Point_2)
#平面直线与X轴的夹角[x1, y1] -- [x2, y2]
circle(Point_1, Point_2, Point_3)
#圆 三点成圆
#以确定的三点表示圆的方程，得到圆心和半径 [x1, y1] -- [x2, y2] -- [x3, y3]
crossPointOfTwoLine(Line_1, Line_2)
#两直线交点 Line_1:[Point_1, Point_2], Line_2:[Point_1, Point_2]
distance2D(Point_1, Point_2)
#两点之间
#平面两点的距离[x1, y1] -- [x2, y2]
interceptOfLine(Point_1, Point_2)
#平面直线的截距[x1, y1] -- [x2, y2]
lcCrossPoint2D(Line, Circle)
#直经与圆的交点
lcDistance2D(Line, Circle)
#直线到圆的距离
lineDistance2D(Line_1, Line_2)
#两直线距离 Line_1:[Point_1, Point_2], Line_2:[Point_1, Point_2]
parallelCheck(Line_1, Line_2)
#两直线之间
#两直线是否平行 Line_1:[Point_1, Point_2], Line_2:[Point_1, Point_2]
perpendicular(Line)
#求直线的中垂线
plDistance2D(Point, Line)
#点到直线的距离
pointFromCircle(Point, Circle)
#判断点和圆的距离 Point:[x, y], Circle: [[x1, y1], [x2, y2], [x3, y3]]
pointInLine(Point_1, Point_2, Point_3)
#判定三点共线
slope(Point_1, Point_2)
#平面直线的斜率[x1, y1] -- [x2, y2]
tangencyPoint(Point, Circle)
#过圆外部一点，得到与圆的切点的坐标 Point:[x, y], Circle: [[x1, y1], [x2, y2], [x3, y3]]
</span>
这个是解三角形的工具：
<span style="font-size:18px;">###
# @usage 解三角形
# @author mw
# @date 2016年04月16日 星期六 07:50:31
# @param 三角形六元素 [边1， 边2， 边3, 角1, 角2, 角3]，角为边所对的角，角度制
# @return 三角形的三个顶点坐标
#
###
#解三角形, 传入array为[三边，三角]按顺序排列的六元素数组
#边和角是对边和对角的关系排列
#待求量用'?'表示， 如[3, 4, 5, '?', '?', '?']为求三个角
def solveTriangle(elementArray):
elements = len(elementArray);
if (elements != 6):
return [];
unknows_1 = unknows_2 = 0;
for i in range(6):
if (elementArray[i] == '?'):
if (i < 3):
unknows_1+=1;
else:
unknows_2+=1;
if (unknows_1 >= 3 or unknows_1+unknows_2 > 3):
return [];
#已知三边
if (unknows_1 == 0):
for i in range(3):
if (elementArray[(i+1)%3]+elementArray[(i+2)%3] <=elementArray[i]):
return [];
return know3edges([elementArray[2], elementArray[0], elementArray[1]]);
#
if (unknows_1 == 1):
#用余弦公式的情况
for i in range(3):
if (elementArray[i] == '?' and
(elementArray[(i+1)%3] != '?' and elementArray[(i+1)%3+3] == '?') and
(elementArray[(i+2)%3] != '?' and elementArray[(i+2)%3+3] == '?')):
b = elementArray[(i+1)%3];
c = elementArray[(i+2)%3];
A = elementArray[i+3];
a = math.sqrt(b*b+c*c-2*b*c*math.cos(A/180*math.pi));
elementArray[i] = a;
break;
if (elementArray[0] != '?' and
elementArray[1] != '?' and
elementArray[2] != '?'):
return know3edges([elementArray[2], elementArray[0], elementArray[1]]);
#至少两个角已知， 可以把三个角都求出来
if (unknows_2 == 1):
for i in range(3):
if (elementArray[i+3] == '?' and
elementArray[(i+1)%3+3] != '?' and
elementArray[(i+2)%3+3] != '?'):
elementArray[i+3] = 180-(elementArray[(i+1)%3+3]+elementArray[(i+2)%3+3]);
break;
#能使用正弦公式的各种情况
#正弦公式a/sinA = b/sinB = c/sinC = sinValue
sinValue = 0;
for i in range(3):
if (elementArray[i] != '?' and elementArray[i+3] != '?'):
sinValue = elementArray[i]/math.sin(elementArray[i+3]/180*math.pi);
break;
#由已知两边一角或三角一边 => 两边两角或三边三角
for i in range(3):
if (elementArray[i] == '?' and elementArray[i+3] != '?'):
elementArray[i] = sinValue * math.sin(elementArray[i+3]/180*math.pi);
if (elementArray[i] != '?' and elementArray[i+3] == '?'):
elementArray[i+3] = math.asin(elementArray[i]/sinValue)/math.pi*180;
if (elementArray[0] != '?' and
elementArray[1] != '?' and
elementArray[2] != '?'):
return know3edges([elementArray[2], elementArray[0], elementArray[1]]);
#如果还有角未求得
for i in range(3):
if (elementArray[i+3] == '?'):
elementArray[i+3] = 180-(elementArray[(i+1)%3+3]+elementArray[(i+2)%3+3]);
break;
#由角求边
for i in range(3):
if (elementArray[i] == '?' and elementArray[i+3] != '?'):
elementArray[i] = sinValue*math.sin(elementArray[i+3]/180*math.pi);
#校验
for i in range(3):
if (elementArray[i+3] <= 0):
#角度为负或0, 说明给的条件不足以构成三角形
return [];
return know3edges([elementArray[2], elementArray[0], elementArray[1]]);
#已知三角形三条边求六元素
def know3edges(edges):
if (len(edges) <= 0):
return [];
#角A
A = math.acos((edges[1]*edges[1]+edges[2]*edges[2]-edges[0]*edges[0])/(2*edges[1]*edges[2]));
#角B
B = math.acos((edges[0]*edges[0]+edges[2]*edges[2]-edges[1]*edges[1])/(2*edges[0]*edges[2]));
#角C
C = math.acos((edges[0]*edges[0]+edges[1]*edges[1]-edges[2]*edges[2])/(2*edges[0]*edges[1]));
A = A/math.pi*180;
B = B/math.pi*180;
C = C/math.pi*180;
return [edges[1], edges[2], edges[0]]+[B, C, A];</span>
本节到此结束，欲知后事如何，请看下回分解。