Kmeans聚类Python程序

之前写过两个关于kmeans的博客
kmeans理论介绍
kmeans与dbscan的对比

再说下算法的过程：
1.随机的选取k个聚类中心，这个k是有自己设置的
2.计算数据集到k个聚类中心的距离
3.对一条数据，分配到距k个聚类中心最近的类中
4.得到新的k个数据，计算聚类中心
5.更新2,3,4当类别不再变化时结束迭代

Python程序
计算欧式距离

    # 计算欧式距离
def distEclud(vecA,vecB):
    return sqrt(sum(power(vecA-vecB,2)))

随机的选取初始类中心

    # 随机的参数k个类中心
def randCent(dataSet,k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))
    # 中心是在每一维的最大值和最小值之间随机选取
    for j in range(n):
        minJ = min(dataSet[:,j])
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = minJ + rangeJ * random.rand(k,1)
    return centroids

kmeans算法过程

    # 聚类过程 根据欧式距离判定数据所在的类，距离越近越好 
def kMeans0(dataSet,k,distMeas = distEclud,creatCent = randCent):
    # m个样本，n个特征 
    m,n = shape(dataSet)
    print m,n 
    # 记录每个数据的类别，以及到所在类别中心的距离
    clusterAssment = mat(zeros((m,2)))
    centroids = creatCent(dataSet,k)
    clusterChanged = True 
    # 当类别不在变化时候停止迭代
    while clusterChanged:
        clusterChanged = False
        # 遍历所有的样本数据
        for i in range(m):
            minDist = inf   
            minIndex  = -1
            # 计算 第i条样本到k个类中心的距离
            # 以最小的类别，更新该样本所在的类别
            for j  in range(k):
                disJI = distMeas(centroids[j,:],dataSet[i,:])
                if disJI < minDist:
                    minDist = disJI
                    minIndex = j 
            if clusterAssment[i,0] != minIndex: 
                clusterChanged = True
            clusterAssment[i,:] = minIndex ,minDist
        # print centroids
        # 计算结束的k个类的类中心 
        for cent in range(k):
            ptInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
            centroids[cent,:] = mean(ptInClust,axis=0)
    return centroids,clusterAssment

缺点：
1.随机的选取类中心，可能影响聚类的效果，这个博客有详解
2.每次计算的都是欧式距离，于是乎，可以更换其他距离的公式试试效果如何
下面采用的是余弦相识度类来计算一个样本到类中心的距离。
余弦相识度计算公式：

这其实就是两个向量的夹角的余弦值，在[-1.1]之间，至于如何衡量距离的好坏，可以认为在1 和-1附近是好的，也可以认为是1附近是最好的，毕竟在-1附近是向量方向相反了。
更改上面的程序，认为余弦相识度越接近1认为越可能是同一类。
Python程序：

    # 计算余弦相识度
def cosineSimilarity(vecA,vecB):
    vecA = array(vecA)
    vecB = array(vecB)
    a = sum(vecA*vecB)
    b = sqrt(sum(vecA*vecA))
    c = sqrt(sum(vecB*vecB))
    if b!=0 and c!=0:
        return a/(b*c)
    if b!=0 and c==0 :
        return a/(b*0.001)
    if b==0 and c!=0:
        return a/(c*0.001)

上面当两个向量中有一个模为0的时候认为是0.01
聚类程序：

    # 聚类过程 根据余弦相识度判定 数据与类中心相识度越高 作为所在的类 
def kMeans1(dataSet,k,distMeas = cosineSimilarity,creatCent = randCent):
    m,n = shape(dataSet)
    print m,n 
    # 记录每个数据的类别，以及到所在类别中心的距离
    clusterAssment = mat(zeros((m,2)))
    centroids = creatCent(dataSet,k)
    clusterChanged = True 
    # 当类别不在变化时候停止迭代
    while clusterChanged:
        clusterChanged = False
        # 遍历所有的样本数据
        for i in range(m):
            maxDist = -1  
            maxIndex  = -1
            # 计算 第i条样本到k个类中心的距离
            # 以最小的类别，更新该样本所在的类别
            for j  in range(k):
                disJI = distMeas(centroids[j,:],dataSet[i,:])
                if disJI > maxDist:
                    maxDist = disJI
                    maxIndex = j 
            if clusterAssment[i,0] != maxIndex: 
                clusterChanged = True
            clusterAssment[i,:] = maxIndex ,maxDist
        # print centroids
        # 计算结果的k个类的类中心 
        for cent in range(k):
            ptInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
            centroids[cent,:] = mean(ptInClust,axis=0)
    return centroids,clusterAssment

载入数据：

# -*- coding: utf-8 -*-
from numpy import *
import sys   
sys.setrecursionlimit(5000) #例如这里设置为一百万

def loadDataSet(filename):
    dataMat=[]
    fr = open(filename)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float,curLine)
        dataMat.append(fltLine)
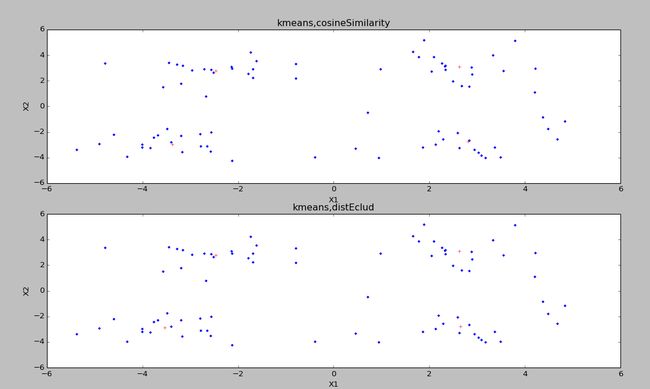
    return mat(dataMat)

根据数据集运行的结果

这是最好的聚类结果，运行多长发现，根据余弦相识度的聚类也可能出现不好的结果，但是整体比欧拉距离的好点。

画图程序：

def plotKmeans(k):
    import matplotlib.pyplot as plt
    dataSet = loadDataSet('testSet.txt')
    # 余弦相识度
    center1,cluserAssment = kMeans1(dataSet,k,distMeas = cosineSimilarity,creatCent = randCent)
    print center1
    plt.figure(1)
    plt.subplot(211)
    plt.plot(array(dataSet[:,0]),array(dataSet[:,1]),'.')
    plt.plot(array(center1[:,0]),array(center1[:,1]), 'r+')
    # plt.annotate('local max', xy=(2, 1), xytext=(3, 1.5),
                # arrowprops=dict(facecolor='red', shrink=0.05),)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.title('kmeans,cosineSimilarity')
    plt.subplot(212)
    # 欧拉距离
    center0,cluserAssment = kMeans0(dataSet,k,distMeas = distEclud,creatCent = randCent)
    print center0
    plt.plot(array(dataSet[:,0]),array(dataSet[:,1]),'.')
    plt.plot(array(center0[:,0]),array(center0[:,1]), 'r+')
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.title('kmeans,distEclud')

    plt.show()