指令选择器调查(4)
3.5. 动态规划优化模式选择
在1985年Aho与Ganapathi【6】展示了一个称为CGL的语言,它提供了一个Glanville-Graham风格的记法来描述模式。描述送到一个预处理器,产生一个可以被包括在编译器后端的指令选择器。指令选择器以Aho-Corasick算法为基础进行模式匹配,包含了Aho与Johnson之前使用的动态规划(DP)技术的一个简化版。指令选择器在输入树上执行三个遍:两个自底向上遍——第一个用于标记模式匹配的节点,第二个用于计算最优选择;以及一个流出代码的自顶向下遍。每个遍执行显示出O(n)的时间复杂性,因此在线性时间内产生最优指令选择。
DP算法的概要(不包括模式匹配部分)在图3.11中给出。每个节点维护一个标记及两个向量——costs与matches。在产生式“l ← tree”中非终结符l用作索引,costs[l]给出归纳到l的代价最低的规则,matches[l]给出该规则的索引。在这个上下文里规则与模式持有相同的含义,它们将互换地使用。对于一个给定的节点n,算法遍历n的匹配集中所有的模式。如果相比当前最好的选择,这个模式严格地以一个更低的代价归纳到一个非终结符l,那么更新向量以反映这更好的选择。应用一个模式p的代价就是模式自身的代价加上匹配p的v个节点的模式的代价。因而使用一个辅助函数cost(t, n)来方便这个代价的计算。因为某些规则可能是链式法则——即一个替代符号被重写为另一个——规则被遍历的次序必须是这样:如果某些节点被修改了,之前检查过的规则不需要重新检查。例如,如果在匹配集中产生式“s ← r”与“t ← s”存在两个规则,那么首先应该检查“s ← r”,因为它可能降低“t ← s”所依赖的代价。这个做法被Aho等【7】改进并扩展为一个称为twig的著名的树操作框架(一个早期的参考手册在【224】可以得到)。图3.12中给出了几个以twig表示的加法规则。
这个动态规划设计比起线性化语法解析,有几个好处:
· 归纳冲突被DP算法自动处理,因此消除了之前规则次序对代码质量的影响。
· 不再需要显式地打破规则集中的环,在基于Glanville-Graham的指令选择器中,这会造成无限循环。
· 机器描述更简洁,因为仅在代价上不同的规则可以更容易地重构为单条规则,只带有不同的代价及动作。
结果,这导致了一个更简单、更小的机器描述。例如,Aho等报告VAX机器的整个twig描述仅使用了115个规则。
Twig的几个改进随后由Yates与Schwartz【242】及Emmelmann等【75】做出。Yates与Schwartz把twig的Hoffmann-O’Donnell的模式匹配算法的自顶向下版本,替换为匹配更快并扩展属性支持以允许更强大谓词的自底向上的版本。Emmelmann等实现了一个称为BEG的后端生成器,它包括了伴随IR树构建并行运行的一个DP算法改进版本。另外,BEG把辅助函数代码内联进算法。类似的改进也由Fraser等【98】在实现IBURG时做出,它更简单(950对比3,000行C代码),比twig快25倍。随后Gough与Ledermann【114,115】对IBURG进行少量改进,实现了MBURG,而且IBURG已经被以各种编程语言重新实现(即用于Java的JBURG【222】,及用于C++的OCamlBURG【225】)。
Tjiang【223】[1]把twig与IBURG的思想整合进了OLIVE(这个名字是twig的副产品)。Tjiang也做出了几个额外的改进,比如允许规则使用任意的代价函数。而不是固定的数值。通过返回无限的代价,依赖于当前的上下文,规则可以被动态停止使用,这允许更通用的指令选择。
3.6. 预计算代价
在之前展示的动态规划的做法里,模式匹配算法完全是表驱动的,而用于模式最优选择的代价计算在代码生成时执行。正如我们将看到的,这些运算也可以预先计算并整合进表中。我们将这称为线下代价分析。
直觉是,与使用标记解析输入树以找出所有匹配模式的方式相同,也可以创建状态来解析输入树以找出最优的选择。一个状态不仅代表一棵特定子树的匹配集,还代表最优地把该子树归纳到任意给定非终结符的模式集。这里理解的关键是,这不意味着根节点处的状态携带了这棵树的信息。事实上,这样的尝试要求数量无限的状态。相反,一个状态仅表示在根节点处应该应用哪个规则,使得子树的后续规则选择将共同为整棵树产生一个最优的模式选择。随着继续我们的讨论,这会更加清晰。
从现在开始,假定我们有一组表StateTablei,对于一个特定的操作符i,它给出了下一个状态;以及一张表RuleTable,它给出用于一个给定状态和目标的规则。那么模式匹配与最优模式选择完全可以表驱动,因此避免了在运行时依靠动态规划计算代价。对这样一个指令选择器,图3.13给出了伪代码。
根据文献,Henry【128】[2]首先在他的博士论文里讨论了这个想法,但实际尝试它的先驱是Hatcher与Christopher【124】。这个做法看起来相当不为人知,因为它很少被引用,但从收集到的信息——这是Hoffmann与O’Donnell的自底向上算法的一个扩展——算法工作如下。一开始,强制通过一张额外查找表,增强模式匹配器来处理交换性。在模式匹配遍之后,根据哪些标记被分配给了节点,执行一个选择模式的自顶向下遍。这通过查询另一组表matchsettab——使用当前节点的标记及一个非终结符作为索引——来完成。因此这类似于DP做法里,在代价被计算出来后,如何进行模式的选择。
那么问题是如何计算表matchsettab。首先,因为预处理器构建包含图,它也收集了把模式p转换到另一个被p包含的模式q的代价。这通过递归地使用其他模式改写p直到它等于q。这个代价就是所有被使用模式的代价总和。我们把这个代价以函数reducecost(p q)来表示。现在,计划是选择以最低代价将根节点是给定标记的一棵子树归纳到一个特定的非终结符的规则。Hatcher与Christopher通过首先构建该标记最大的表示树R——这通过重叠匹配集中的所有模式来实现——然后选择使得reducecost(R x) = reducecost(R z.rhs) +z.cost的规则z来着手这个问题 。这将要么选择最大的模式,或者如果存在,一个较小、导致较低代价的模式。不过,如果存在无关的模式,就不能总是保证最优,要求手工调整语法。
[1]基于来自【159】与【38】的第二手资料。
[2]基于来自【23】的第二手资料。

处理线下代价分析的另一个做法由Pelegrí-Llopart与Graham【183】提出。在他们的原创性论文里,Pelegrí-Llopart与Graham提倡一个做法,其中输入树是逐渐地重写为更小的树,直到只留下单个节点。作者证明可以安排树重写使得它仅发生在树的叶子上,导致一个自底向上的重写系统(BURS)。重写系统的一个例子在图3.14(a)中给出,使用BURS可以表示大多数机器描述。使用BURS的原理,Pelegrí-Llopart与Graham设计了一个计算最优模式选择所需要的表算法。作者报告说他们的实现生成的表仅比Glanville-Graham方案生成的表大一点,产生几乎快2倍的优化代码,且比twig快超过5倍。
想法如下。对于一棵给定的树,形成一个局部重写图(LR图)使得节点代表中间子树,边代表一个特定重写规则的应用。图3.14(b)中给出这样一个图的例子。把某些节点设置为目标(即树重写期望的终节点),从LR图选择一个子图使得重写可能性的数目是最小的。因为这是一个NP-完全问题,Pelegrí-Llopart与Graham应用了一个启发式迭代地删除被认为“无用”的节点。结果子图称为唯一可逆转LR图(UI LR图)。每个UI LR图对应一个状态,所有的状态可以通过生成所有可能输入子树的LR图来计算。
为了包含最优模式选择,扩充LR图使得每个节点不再是一个模式(即一棵子树),而是一个(p,c)对,其中c代表到达模式p的最小代价。一个朴实的做法是在状态中包括到达一个特定模式的全部代价。不过,依赖于重写系统,这可能要求无限数量的状态;尽管这不是真实机器的典型特征,图3.15(b)给出了这样的一个例子。一个更好的方法是使用选中模式的相对代价。即把c计算为p的代价与LR图中其他任意模式的最小代价的差值。这产生了相同的最优模式选择,但所需状态的数量显著减少(参考图3.15(c))。这个代价称为delta代价,被扩充的LR图被称为δ-LR图。为了限制数据的大小,Pelegrí-Llopart与Graham使用Chase算法的一个扩展来生成δ-LR图。

图3.14:BURS例子(来自【183】)
图3.15:转换代价入状态(来自【183】)
自其发表,许多后续的论文错误地以BURS理论来谈论线下代价分析的思想。确实,Pelegrí-Llopart与Graham是第一个提出一个高效、可行的方法,使得线下代价分析成为表驱动最优指令选择的一个可行的方案。不过,线下代价分析与BURS理论实际上是正交的;就像我们将要看到的,存在生成更简单且更有效状态表的其他方法。
这样一个方法由Balachandran等【23】提出。不像Pelegrí-Llopart与Graham,他们的做法依赖于传统的产生式规则语法,而不是重写系统。另外,他们的表生成器更简单、更高效,因为它直接生成状态的最小集,而不是首先枚举所有可能的状态,然后尝试裁剪它们。Balachandran等的一个主要贡献是引入了线性形式语法(linear-form grammar)。这要求每个规则属于下面类别之一:
· n0 → op(n1, . . .,nk) ——其中ni都是非终结符,op是参数数目k > 0的一个操作符,
· n → T——其中n是一个非终结符,T是一个终结符(这可以看做第一个类别的一个特殊版本,其中k=0,),或者
· n → m——n与m都是非终结符。
前两个类别统称基本规则,而最后的类别称为链规则。通过引入新的非终结符与实现必要转换的规则,一个非线性语法可以很容易地重写为线性形式,即:
规则 代价 规则 代价
reg → ▴(+(Reg,Reg)) 2 reg → ▴(n1) 2
n1 → +(n2,n2) 0
n2 → Reg 0
原始语法 è 正常形式语法
线性形式语法的好处是每条规则在输入树中最多仅向下扩展一层。因此简化了算法,因为它们不需要考虑选择一条规则可能迫使某些节点被跳过的情形。
本质上,Balachandran等的表生成算法通过首先为所有可能的叶子节点生成状态,然后从已存在的状态迭代地计算新状态来运行。这个思想还被Proebsting【187,188】采用。因为两种做法本质上是类似的,除了Proebsting提供了一个更简单、更详细的解释,我们将以后者来继续我们的讨论。不过,在本报告中,我们将仅给出算法的概要;建议感兴趣的读者查阅【188】,它给出了一个详细的描述。
就像Balachandran等人,Proebsting的表生成器假定语法是线性形式的,因为这简化了算法。该算法围绕一个包含了考虑中状态的工作队列。一开始,这个队列是空的,并以从所有可能叶子节点生成的状态初始化。每个状态规范化它的代价,使得任何适用的规则在该状态下的最低代价是0,然后把所有适用的链规则加入该状态(这称为计算迁移闭包)。两个状态是相同的,如果每个非终结符的选中代价及规则是相同的。然后,对于从队列弹出的每个状态,算法实际上模拟,如果一组节点以弹出的状态来标记,与已经存在的节点形成的任意组合,并作为某个操作符节点的子节点,会发生什么(参考图3.16)。如果被标记子节点的这样一个组合表示一个未曾见的状态——即相比已有的状态,某些非终结符的选中规则或节点是不一样的——这个新状态承诺已有的状态并被加入队列中。当队列变为空时,该算法终止,这表示所有感兴趣的状态已经被生成。Fraser等【99】在一个著名的称为Burg[1]的代码生成系统上实现了这个算法,自引入以来,Burg在编译器社区已经引领了命名约定,我称之为Burger现象[2]。
如果减少生成状态的数量,可以提升表生成器的速度。Henry【127】[3]进行了最初的尝试,稍后由Proebsting【187,188】改进并推广。Proebsting发展了两个方法来减少生成状态的数量:状态修剪(statetrimming),它扩展、推广了Henry的方法;链规则修剪(chain rule trimming)。前者通过清除证明不会参与最低代价覆盖的非终结符的信息,增加了两个创建状态相同的可能性。后者通过尽可能使用相同的规则,进一步最小化状态的数量。该算法由Kang与Choe【136,137】进一步改进,他们充分利用了通用机器描述的性质,以减少重复的状态测试。
[1] BURG与IBURG之间的联系始于IBURG开始作为一个语法说明的测试平台,该语法后来为BURG使用。因为应用在IBURG中的某些想法显示了某些好处,Fraser等把IBURG改进、扩展为一个独立的指令选择生成器。
[2] 在为这篇评论进行研究时,我遇到了以下这些:BURG【99】,CBURG【202】,DBURG【80】,GBURG【97】,IBURG【98】,JBURG【222】,HBURG【218】,LBURG【122】,MBURG【114,115】,OCamlBURG【225】,及WBURG【189】。
[3] 基于来自【187】的第二手资料。

因此,将线下代价分析与自底向上树模式匹配合并起来的想法已经在许多编译器相关系统中实现了。其他一些著名但还没提及的程序包括:Hatcher与Tuller的UNH-Codegen【126];Engler与Proebsting的DCG【78】;Hanson与Fraser的LBURG【122】;及Proebsting与Whaley的WBURG【189】。Burg还有一个Haskell版本,叫做HBURG【218】。
3.7. 两全其美
基于DP及表驱动的指令选择器都有各自的优缺点。前者——应用一个规则的全部代价在代码生成期间计算——具有能支持动态代价的好处,即一个模式的代价依赖于上下文而不是静态不变。相比用更长预处理时间换取更快代码生成的纯表驱动的同类,它要慢得多。不过,因为这些表,这样的指令选择器有大得多的倾向,生成它们非常费时;对于病态语法,这可能是不可行的。另外,特定规则的代价必须是固定的。
Ertl等【81】发现了一个方法,整合了这两个技术的优点以补偿它们各自缺点。直觉上是这样的:不是预先生成所有的状态,在一棵给定的输入树上仅生成必要的状态以执行指令选择。这通过在代码生成期间按需创建状态来实现。当遇到一棵新的子树时,使用动态规划创建处理该子树所要求的的状态。然后对在输入程序中可能出现的其他相同的子树重用这些状态,这样分摊了生成状态的开销。因此,不像之前状态计算作为编译编译器的一部分——因而必须为所有可能的输入树计算状态——在这个方法中的状态仅需要处理单棵子树。这导致短得多的状态生成时间及更小表——实际上,它与单纯的基于DP的解决方案出于同等水平——使得它能够处理更大、更复杂的机器描述。另外,相比一个完全表驱动指令选择器,在重用状态时开销是最小的。Ertl等还通过一旦根节点代价改变,就重写计算及排序哈希表中的状态,扩展了这个想法来处理动态代价。尽管这导致了额外的开销,它仍然比纯粹基于DP的实现要快。
3.8 . 其他基于树的做法
. 其他基于树的做法
Ganapathi【103】尝试整合树重写、语法分析、自动化驱动树模式匹配,并以逻辑编程语言Prolog实现了一个系统进行研究。这个方案允许指令选择被扩展为DAG(下一章会更多地讨论这个话题),但在最坏情形下执行时间是指数级的。
Giegerich与Schmal【110】把指令选择的问题重新阐述为“一个派生层次的问题”(problem of a hierarchic derivor),还把同时代的某些做法重新措辞为这样的问题。以简短的术语来说,这需要指定及实现一个机制“γ:T(Q) → T(Z)”,其中T(Q)与T(Z)分别表示以中间及机器语言表示程序的代数项(term algebras)。因此,γ可以被视为指令选择器的结果。不过,机器描述通常包含规则,其中依照Q来表达Z中的每条机器指令;因此我们可以把机器说明视为一个同态“δ:T(Z) → T(Q)”。指令选择生成器的任务就是通过反置δ来推导γ(即通过模式匹配技术)。要获得最优的指令选择,每当某个“q∈T(Q)”具有数个“z∈T(Z)”使得“δ(q) = z”,生成器还必须把δ−1的构造与一个选择函数ξ交错。感兴趣的读者建议参考论文。
通过提供一个代数框架,Giegerich与Schmal的目的是允许形式化描述代码生成的方方面面——不仅是指令选择,还有指令调度及寄存器分配,以简化机器描述并使得完整性及正确性的证明成为可能。Despland等【63】提出了类似的,基于重写技术的做法,Dold等【67,246】使用抽象状态机,发展了证明这样描述的正确性的技术。不过,这些思想没有引起注意,因为文章的引用数充其量是有限的。
在一个解决硬件检验的尝试里,Nowak与Marwedel【179】发展了一个方法,其中机器被塑造成一张图,在这张机器图上匹配输入程序(表示为树)。这里提到他们的论文仅是为了完整性,因为该做法把代码生成整合为一个整体(即还包括了调度及寄存器分配)但甚少关注指令选择。
Hatcher【125】开发了一个称为UCG的系统实现了一个类似于Pelegrí-Llopart与Graham的做法,但依赖于逻辑方程,而不是BURS理论。这两个记法是紧密联系的,两者都应用了一组预定义的规则来把输入程序重写为单个目标项。不过,在作为逻辑方程给出的机器描述中,其所有的转换规则都基于一组内置的操作。内置操作具有一个代价及表示为代码流出的隐含语义。一个规则的代价等于该规则中使用的所有内置规则代价的总和,因此避免了手动为每条规则使用代价。此外,在UCG中没有预定义的内置操作,而是作为逻辑方程的部分给出。这为描述机器提供了一个非常通用的机制。通过把描述带有代价的匹配状态重新计算为表,对于给定的输入程序也实现了规则的最佳使用。不过,这个工作似乎没有效果或极有限。
指令选择问题的另一个重新阐述由Ferdinand等【88】给出。Ferdinand等把该问题简化为一个有限树自动机,并通过应用该领域已有的理论,概括了之前由Hoffmann与O’Donnell以及Pelegrí-Llopart与Graham发明的基于状态的模式匹配算法。Ferdinand等还展示了基于子集构造的几个新算法,它们从指令选择生成有限树自动机。不过,论文缺少足够的实验数据以及与同时代做法的比较,这使得判断其重要性变得困难。后来Borchardt【27】通过以树系列换能器(tree series transducers)替换树自动机扩展了这项工作,但在这里其重要性也是不清楚的。
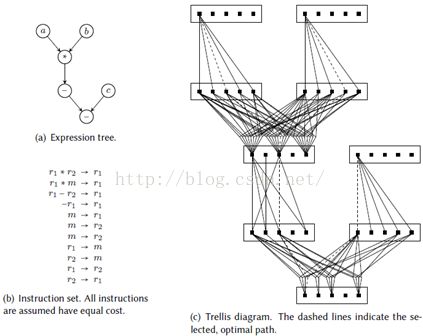
指向数字信号处理器,Wess【236】特别地提出一个使用栅格图以整合指令选择与寄存器分配的方法。输入树首先被转换为一个栅格图,对于表达式树中任意给定节点,它实质上捕捉所有可用机器指令及寄存器的使用。栅格图中的每个节点包含一个最优值数组(OVA),其中每个元素表示保存在内存或一个特定寄存器的数值。元素的值表示从叶子到该节点的最低累计代价。如果保存在寄存器中,该元素还表示其他哪些寄存器可用,这意味着该数组的大小是2n−1+1(目标寄存器必须可用,并假定每条指令仅写一个寄存器),其中n是目标机器上寄存器的数目。例如,对于一个有两个寄存器 r1与r2的机器,OVA是

其中TL(i)代表数值的目标位置,而RA(i)代表可用的寄存器(例子取自【236】)。使用这个设置,在栅格图中为表达式树的每个中间节点生成一个节点。对每个叶子节点产生两个栅格图节点来处理使用前首先需要转换到另一个位置的输入值的情形。将en(i)表示为在节点n处的OVA元素i。对于一元操作节点,如果存在一个实现这个一元操作且由em(i) 产生en(j)的值的指令序列,在en(i)与em(j)之间生成一条边。类似的,对于二元操作节点,如果存在这样一个对应的指令序列,从en(i)及nm(j)到eo(k)生成一对边。 这可以推广到n元操作。那么对一棵特定的表达式树查找最优代码就简化为查找从每个叶子到根节点的一条路径,使得最终值保存在一个位置,该位置对应的OVA元素在根节点是最小的。图3.7给出了一个例子。因为栅格图依赖于目标机器,重指向通过修改栅格图形成的方式来完成。尽管栅格图允许处理非对称寄存器以及同时进行指令选择与寄存器分配,其处理时间是状态数的指数倍。Fröhlich等【101】进行了改善,使栅格图按需构建。不过,不能模仿复杂的指令,因为这个做法假设表达式与机器指令间是一一映射的。
图3.17:对于正文中描述的2寄存器的目标机器,应用于表达式-(a * b) – c的一个栅格图。假定变量a,b及c一开始保存在内存中。
由Shu等【210】应用遗传算法理论【198】开发了一个非常规的技术。想法是把一个解决方案表示为一个DNA字符串,称为染色体,然后分裂、合并及突变现有的解决方案(希望)以更好的一个方案结束。至于指令选择的问题,Shu等把染色体表示为二进制字符串,其中1表示选择一个特定的模式。因此每个染色体的长度等于在一棵给定树中匹配的模式实例的数目。每个染色体由一个有限函数评估,这个函数被定义为
其中k是某个大于1的常量,f1是选中模式的个数,f2是被多个选中模式所覆盖的节点数。因此目标是最大化适应值。这通过使比特字符串受制于标准GA操作来实现(即合理成比例复制(fitness-proportionate reproduction),单点交叉(single-point crossover),一点突变(one-bit mutations)等;参考Goldberg【112】)。不过,论文中的实验数据是贫弱的:测试案例限制在仅从两个算法得到的中等大小的基本块(至多50个节点);这个做法的重要性不清楚。
Bravenboer与Visser【32】应用基于规则的程序转换系统的策略(近期的调查参考【230】)来解决指令选择。使用一个称为Stratego的系统【231】,模式选择器可以被定义为机器描述的部分,允许它被裁剪为指令集。在他们的论文里,称这为提供了一个重写策略。该系统允许方法的建模,比如穷举搜索、最大咀嚼及动态规划。不过,纯表驱动技术如合并线下代价分析显然是不支持的。因此,理论上Stratego可以合并几个模式选择技术,但Bravenboer与Visser没有提供一个有用的例子。
3.9. 应用[1]
多年以来,应用树覆盖的代码生成系统在许多编译器中得到广泛的使用。让我们看一些例子。Araujo与Malik【16】使用OLIVE尝试把指令选择与调度及寄存器分配整合起来。由Leupers与Marwedel【160,169】开发的RECORD编译器使用IBURG,类似于Kreuzer等【151】开发的REDACO,工作在栅格图上的编译器。Pagode编译器,由Canalda等【37】开发,应用了BURS理论的一种形式。Spam,一个应用了OLIVE,在Princeton开发的DSP定点处理器编译器。CoSy编译器应用BEG的一个改进版本[2]。Boulytchev【28】改写Burg来辅助指令集选择。最后,Lburg用在lcc(Little C Compiler)里,由Hanson与Fraser【122】编写,还有Brandner等【31】,他们开发了一个结构化架构描述语言,从中可以自动推导机器指令。
3.10. 总结
在本章我们看了若干基于树覆盖,或以这样那样方式工作在树上的做法。相比宏扩展,这些做法允许使用更复杂的模式,因此产生更有效的指令选择器;通过应用动态规划,可以在线性时间产生最优代码。几个技术还将线下代价分析整合入表生成器,进一步加速了代码生成。换而言之,这些做法是非常快非常高效的,并支持许多机器的代码生成。因此,树覆盖成为最著名的指令选择方法——即使也许不再最适用。
不过,所有这些方法具有两个内在的缺点。第一个缺点与表达式建模相关。因为树的本质,公共子表达式不能被正确地建模。例如,以下代码
[1] 本节主要参考了Leuper与Marwedel【159】之前的调查。
[2] 根据【159】及【44】。
不能被构建为一棵树,它没有(i)重复的操作,即比如= (y,+(+(a, b),+(a, b))),或者(ii)分裂为一个树林,即比如= (x, (+(a, b))及= (y,+(x, x))。前者导致指令重复,而后者可能导致关于数据位置糟糕的决定,因为两棵树之间的联系丢失了。因此,基于树覆盖的指令仅当输入树不包含公共子表达式时保证最优选择——在通常情形下不合理的假设,因为这样的表达式远非罕见。另外,这个限制阻止了具有多个输出的机器指令的建模(即同时计算商和余数的divmod指令,或任何设置条件码或状态标记的指令)。
第二个缺点是树不能模拟控制流。例如,一个for语句要求一个回边,这样违反了树的定义。由于这个原因,基于树覆盖的指令选择器仅工作在基本块内的表达式树上,并使用一个单独的方法为控制流流出代码。这结果妨碍了包含任何类型控制流的复杂机器指令的匹配;这样的指令必须要么从机器描述中移除,要么通过属性函数手动处理。另外,在一个局部块域上最优的决策在一个全局函数域上可能是次优的。另一个相关的缺点是覆盖多棵树的机器指令不能被自动匹配或选择,比如SIMD指令。这归咎于状态标记,它一次仅能遍历一棵树;模式选择也一样。最后,本章中描述的做法没有一个可以处理好不符合典型假设的机器指令(即使用了某些额外的资源限制)。
因此,尽管树覆盖方法优于宏展开,以复杂性增加为代价,极大地提高了代码质量,但它假定了在实践中根本不成立的程序结构与机器行为。此外,所有这样的方法都局限在基本块内工作,这可能导致对整个函数而言次优的结果。在下一章,我们将看对付这些问题的方法。