poj1236|poj3177 tarjan,强联通,有向/无向
强连通是指内部任意点出发都能到达其余各点。
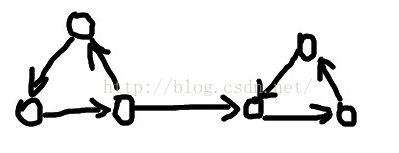
至于这题为什么要用连通块缩点,看完下面这张图就明白了。。
#include<iostream>
#include<algorithm>
#include<string>
#include<map>//int dx[4]={0,0,-1,1};int dy[4]={-1,1,0,0};
#include<set>//int gcd(int a,int b){return b?gcd(b,a%b):a;}
#include<vector>
#include<cmath>
#include<stack>
#include<string.h>
#include<stdlib.h>
#include<cstdio>
#define lowbit(x) (x) & (-x)
#define mod 1000000007
#define ll long long
using namespace std;
#define maxn 105
int n;
vector<int> x[maxn];
int in[maxn],out[maxn];
//tarjan【强连通缩点】模板,【有向】
int dfn_clock,cnt;
int low[maxn],dfn[maxn],instack[maxn],suo[maxn];
stack<int> st;
void init_tarjan(){
for(int i=0;i<n;++i){
instack[i]=1;
}
while(!st.empty()) st.pop();
memset(dfn,0,sizeof(dfn));
dfn_clock=1;
cnt=0; //缩完后图上有几个点
}
void tarjan(int p){
dfn[p]=low[p]=dfn_clock++;
st.push(p);
for(int i=0;i<x[p].size();++i){
int w=x[p][i];
if(!dfn[w]){
tarjan(w);
low[p]=min(low[p],low[w]);
}
else if(instack[w]){
low[p]=min(low[p],dfn[w]);
}
}
if(low[p]==dfn[p]){
while(!st.empty()){
int w=st.top();
suo[w]=cnt; //这个强联通里的点都是这个下标
st.pop();
instack[w]=0;
if(w==p)
break;
}
cnt++;
}
}
int main(){
cin>>n;
init_tarjan(); //别忘
int a;
for(int i=0;i<n;++i){
while(cin>>a&&a!=0){
a--;
x[i].push_back(a); //从i指向a有一条边
}
}
//开始用【tarjan】缩点了!!
for(int i=0;i<n;++i){
if(!dfn[i])
tarjan(i);
}//结束
for(int i=0;i<n;++i){
for(int j=0;j<x[i].size();++j){
int w=x[i][j];
if(suo[i]==suo[w]) continue; //同一个强联通里的,i,w已经看作一个点,再分就没意义了
out[suo[i]]++;
in[suo[w]]++;
}
}
int s1=0,s2=0;
//下面只要计算【缩点后】入度为0的点和出度为0的点各有几个
for(int i=0;i<cnt;++i){
if(in[i]==0)
s1++;
if(out[i]==0)
s2++;
}
if(cnt==1) //整个图缩点后只剩一个点,特判
cout<<1<<endl<<0<<endl;
else
cout<<s1<<endl<<max(s1,s2)<<endl; //缩点后图上入度为零的点都是起点,入度和出度可以用线互消
return 0;
}
【poj3177】给一个无向图,图中每个点都能到达其余各点。现问最少加几条边,使得图中任意两点可以用完全不相同的两条路径到达(一段都不能重合)。
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
//tarjan【双连通缩点】模板,【无向】
const int maxn=5005;//点数
const int maxm=10005*2;//边数,因为是无向图,所以这个值要*2
struct Edge{
int to,next;
bool cut;//是否是桥标记
}edge[maxm];
int head[maxn],tot;
int low[maxn],dfn[maxn],st[maxn],suo[maxn];//suo数组的值是1~cnt
int dfn_clock,top;
int cnt;//边双连通块数
bool instack[maxn];
int du[maxn];//缩点后形成树,每个点的度数
int bridge;//桥的数目
void addedge(int u,int v){
edge[tot].to=v;edge[tot].next=head[u];edge[tot].cut=false;
head[u]=tot++;
}
void init(){
memset(du,0,sizeof(du));
tot=0;
memset(head,-1,sizeof(head));
memset(dfn,0,sizeof(dfn));
memset(instack,false,sizeof(instack));
dfn_clock=top=cnt=0;
}
void tarjan(int u,int pre){
int v;
low[u]=dfn[u]=++dfn_clock;
st[top++]=u;
instack[u]=true;
for(int i=head[u];i!=-1;i=edge[i].next){
v=edge[i].to;
if(v==pre)continue;
if( !dfn[v] ){
tarjan(v,u);
if( low[u]>low[v] )low[u]=low[v];
if(low[v]>dfn[u]){
bridge++;
edge[i].cut=true;
edge[i^1].cut=true;
}
}
else if( instack[v] && low[u]>dfn[v] )
low[u]=dfn[v];
}
if(low[u]==dfn[u]){
do{
v=st[--top];
instack[v]=false;
suo[v]=cnt;
}
while( v!=u );
cnt++;
}
}
int main(){
int n,m;
int u,v;
while(scanf("%d%d",&n,&m)!=EOF) {
init();
while(m--){
scanf("%d%d",&u,&v);
u--;v--;
addedge(u,v);
addedge(v,u);
}
//开始用【tarjan】缩点了!!
for(int i=0;i<n;++i){
if(!dfn[i])
tarjan(i,-1);
}//结束
for(int i=0;i<n;i++)
for(int j=head[i];j!=-1;j=edge[j].next)
if(edge[j].cut)
du[suo[i]]++; //计算每个点的度数
int ans=0;
for(int i=0;i<cnt;i++)
if(du[i]==1)
ans++;
printf("%d\n",(ans+1)/2);
}
return 0;
}