主席树 —— HDU 2665 Kth number

对应 hdu 题目：点击打开链接

Kth number

Time Limit: 15000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 7226    Accepted Submission(s): 2311

Problem Description

Give you a sequence and ask you the kth big number of a inteval.

 

Input

The first line is the number of the test cases. 
For each test case, the first line contain two integer n and m (n, m <= 100000), indicates the number of integers in the sequence and the number of the quaere. 
The second line contains n integers, describe the sequence. 
Each of following m lines contains three integers s, t, k. 
[s, t] indicates the interval and k indicates the kth big number in interval [s, t]

 

Output

For each test case, output m lines. Each line contains the kth big number.

 

Sample Input

   
   
   
   

    
    
    
    1 
10 1 
1 4 2 3 5 6 7 8 9 0 
1 3 2 
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    2
   
   
   
   

 

题意：

        T组数据， 每组数据第一行有两个数 n，m。接下来一行有 n 个数， 接下来 m 行每行有3个数 l， r， k ，表示求区间[l，r] 内第 k 小的数。

思路：

        这里选用的数据结构是主席树，从一个实例开始分析：

        求数组 a[] = {0，7，9，5，100，6，12，1} （设起始下标为 1 ）在区间 [3, 7] 内的第 3 小的数，我们容易看到区间 [3, 7] 内的数为 {9，5，100，6，12}，排下序就是 {5，6，9，12，100} ，第 3 小为 9 ，显而易见；然而，用主席树是这样做的：

        1）离散化

        对数组 a[] 进行升序排序得到数组 b[]

        b[]   =   0，1，5，6，7，9，12，100

       下标 =   1，2，3，4，5，6， 7，  8

        用 b[] 数组中的数对应的下标定义数组 a[]，即 0 对应的下标为 1，7对应的下标为 5 ... 得到

        c[] = {1，5，6，3，8，4，7，2}

        2）建立线段树

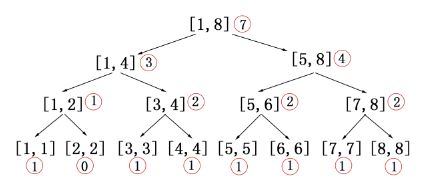
        先分析一个简单的问题，以数组 c[] 的值域（即1~8，这必然是数组长度，同时这也说明了要离散化的原因，因为如果不离散化的话，区间会非常大！）为区间建立线段树，线段树区间维护的是该区间内的值在数组 c[] 中出现了多少个。 

        我们得到：

        其中红色圆圈内的数表示对应区间范围内包含了多少个数组 c[] 里的数，只要懂线段树，就不难计算数组 c[] 中第 k 小的数，比如求数组 c[] 中第 6 小的数，它就应该沿着 [1,8] -> [5, 8] -> [5, 6] -> [6, 6] 找到第 6 小的数为 6，通数组过b[] 映射得到数组 a[] 中第 6 小的数为 b[6] = 9。

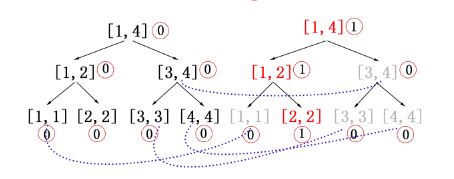
        主席树也是利用这样的方式计算区间第 k 小，只是需要用到的线段树不是一颗，而是 n 颗，而且树的结构完全一样，怎样建树？以数组 c[] 的每个前缀建立如上图的线段树！比如前缀 {1， 5} 建立的线段树和前缀 {1，5，6，3，8，4，7} 建立的线段树分别为：

       数组 c[] = {1，5，6，3，8，4，7，2} 。对于右图，数组 c[] 中前 7 个数在 1~8 中出现了 7 个（即前 7 个数），在 1~4 中出现了 3 个（即 1，3，4），在 5~8 中出现了 4 个（即 5，6，7，8）以此类推 ... 细心点可以发现，它们的圆圈为 1 的叶子刚好是对应的前缀的值。

       我们把左图称为插入了数组 c[] 中区间 [1, 2] 的元素的线段树，右图称为插入了数组 c[] 中区间 [1, 7] 的元素的线段树，我们用右边的树 - 左边的树 （对应区间圈内的数相减），将得到一颗插入了数组 c[] 中区间 [3, 7] 的元素的线段树：  

        然后在这棵树上查找第 3 小的数，将沿着 [1,8] -> [5,8] -> [5,6] -> [6,6] 找到 6，映射到原数组 a[] 就是 b[6] = 9。

        为什么可以相减？由于线段树是开在值域上，区间长度是一定的，所以结构也必然是完全相同的，看着上图，再对照着数组 c[] 中区间 [3, 7] 的数，再仔细想想，就能明白~ 

        这样的思路是正确的，但如果真想把每个前缀都建立一颗完整的线段树是不现实的，空间复杂度太大！这里就要用到可持久化的思想。简单来说就是这样：

        对于 A[] = {2，1，4，3} 这个例子，对每个前缀建树的过程如下：

        第 0 颗，空树，因为还没有添加元素。

       

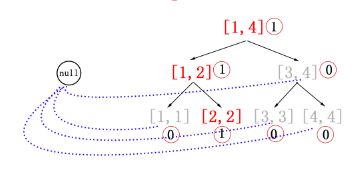
        第 1 颗，即前 1 个元素（值为 2 ），

        我们沿着前一颗树往下找到该元素所在的叶子，我们不是为该前缀建立一颗完整的树，而是对路径经过的每一个孩子都建立一个结点，它的值为前一棵树的值 + 1，另一个孩子的都它前一颗树相同，我们只需要在往下走建立新树的过程中把跟前一颗树完全一样的结点用指针指一下就行了，如图；之后的树以此类推。

        

        这样建树的话，每棵树只需要 logn(树的深度) 个结点，n 棵树的空间复杂度为 n*logn ，是可以接受的。

        这里其实空树的话是可以只用一个结点表示的，因为反正它是空的，结果都是 0。因此也可以按下面的方法建树。

        这道区间第 k 小问题也是主席树的基础应用。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 100010
int node_count;

int lson[20*N];
int rson[20*N];
int count[20*N];
int a[N];
int b[N];
int tree[N];

int q_cmp(void const *_a, void const *_b)
{
    int *a = (int *)_a;
    int *b = (int *)_b;
    return *a - *b;
}

void init()
{
    node_count = 0;
    lson[0] = rson[0] = count[0] = 0;
    memset(tree, 0, sizeof(tree));
}

void build(int *rt, int per_rt, int left, int right, int key)
{
    int mid;
    *rt = ++node_count;
    count[*rt] = count[per_rt] + 1;
    if(left == right){
        lson[*rt] = rson[*rt] = 0;
        return;
    }
    mid = left + (right - left) / 2;
    if(key <= b[mid]){
        build(&lson[*rt], lson[per_rt], left, mid, key);
        rson[*rt] = rson[per_rt];
    }
    else{
        build(&rson[*rt], rson[per_rt], mid + 1, right, key);
        lson[*rt] = lson[per_rt];
    }
}

int query(int lrt, int rrt, int left, int right, int k)
{
    int mid, ct;
    if(left == right)
        return b[left];
    mid = left + (right - left) / 2;
    ct = count[lson[rrt]] - count[lson[lrt]];
    if(k <= ct)
        return query(lson[lrt], lson[rrt], left, mid, k);
    else
        return query(rson[lrt], rson[rrt], mid + 1, right, k - ct);
}

int main()
{
#if 0
    freopen("in.txt","r",stdin);
#endif
    int T;
    scanf("%d", &T);
    while(T--){
		int i;
		int n, m;
		int b_n;
		init();
        scanf("%d%d", &n, &m);
        for(i = 0; i < n; i++){
            scanf("%d", a + i);
            b[i] = a[i];
        }
        qsort(b, n, sizeof(int), q_cmp);
        b_n = 0;
        for(i = 1; i < n; i++)
            if(b[i] != b[b_n]) b[++b_n] = b[i];
        b_n++;
        for(i = 0; i < n; i++)
            build(&tree[i+1], tree[i], 0, b_n - 1, a[i]);
        for(i = 0; i < m; i++){
            int ans;
            int l, r, k;
            scanf("%d%d%d", &l, &r, &k);
            ans = query(tree[l-1], tree[r], 0, b_n - 1, k);
            printf("%d\n", ans);
        }
    }
    return 0;
}