HDU 4565 So Easy! 共轭构造+矩阵快速幂

题意：

A sequence S _n is defined as: 

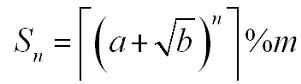这么一个等式，要你算Sn，其中  0< a, m < 2  ¹⁵ , (a-1)  ² < b < a ² , 0 < b, n < 2  ^31；

^{那么计算的时候最大的困难就是向上取整，于是就利用(a-1) 2< b < a2的性质，对向上取整里面添加一个（a-根号b）^n，然后就可以把向上取整直接计算了了。}

^{为什么要这样想呢？ 我们可以发现a+根号b 这个式子的次方是既有整数部分，又有小数部分，同时a-根号b的n次方这个保证是一个小数，且加上去以后，整个括号里面，就变成了整数。整数！你在逗我么？没有。因为你多项式展开，发现a+根号b和a-根号b，对应的位置刚好可以正负完全抵消，剩下的只有整数部分了！这个答案不就是我们需要的向上取整的数吗？没错所以在接一个快速幂。over~}

^{ps:注意初始化的时候int有乘法，不要溢出，及时化成long long。因为这个错误wa了5发TAT。}

^代码：

#include <cstdio>
typedef long long LL;
struct Mat{
    LL m[2][2];
};
inline void E(Mat &s){
    s.m[0][0]=1LL;s.m[0][1]=0LL;
    s.m[1][0]=0LL;s.m[1][1]=1LL;
}
inline void C(Mat &s){
    s.m[0][0]=s.m[0][1]=s.m[1][0]=s.m[1][1]=0LL;
}
inline Mat productMod(Mat a,Mat b,LL Mod){
    Mat s;
    C(s);

    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            if(a.m[i][j])
                for(int k=0;k<2;k++)
                    s.m[i][k] = (s.m[i][k] + a.m[i][j]*b.m[j][k])%Mod;
    return s;
}
inline Mat powMod(Mat a,int b,int Mod){
    Mat s;
    E(s);

    while(b){
        if(b&1) s=productMod(s,a,Mod);
        a=productMod(a,a,Mod);
        b>>=1;
    }
    return s;
}
/**
S<n+1> = 2a*S<n> - (a^2-b)*S<n-1>

m00 = 2a;       m01 = 1;
m10 = (b-a^2);  m11 = 0;
*/

int main()
{
//    freopen("data.in","r",stdin);
    int a,b,n,m;
    while(scanf("%d%d%d%d",&a,&b,&n,&m)!=EOF){
        Mat L,R,re;
        int ans;
        L.m[0][0] = (2LL*(a*a+b))%m;//! 每一个都要存为LL 注意乘法不要溢出
        L.m[0][1] = (2LL*a)%m;
        L.m[1][0] = L.m[1][1] = 0LL;
        R.m[0][0] = (2LL*a)%m;
        R.m[0][1] = 1LL;
        R.m[1][0] = (((LL)b-a*a)%m+m)%m;
        R.m[1][1] = 0LL;
        R = powMod(R,n-1,m);
        re = productMod(L,R,m);
        ans = re.m[0][1];
        printf("%d\n",ans);
    }
    return 0;
}