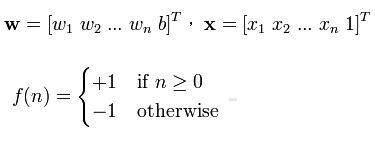人工神经网络（ANN）

来自http://blog.csdn.net/wasd6081058/article/details/7909733

本文将主要参考Tom M.Mitchell的《机器学习》一书说明一下人工神经网络，组织结构是这样的：先讨论人工神经网络最基本的组成单元：感知器和sigmoid单元，然后介绍由这些基本组成的多层次网络的反向算法。

前言：

人工神经网络（Artificial  Neural  Networks)在一定程度上收到了生物学的启发，利用大脑神经元的特征构建出人工神经元来进行数学建模或者计算。神经网络是一种运算模型，由大量的结点和结点之间的连接组成，它除了输入结点以外，每个结点都代表着一种特殊的输出函数，称为激励函数。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重（weight），这相当于人工神经网络的记忆。

第一节. 感知器，线性单元和sigmoid单元

   我们的大脑是有最基本的神经元组成的，这些神经元就是对不同的刺激产生不同的脉冲，我们人类的大脑大约由10^11个神经元互相连接组成，正是由这些种类繁多的神经元，才使得人类有如此神奇的大脑。而我们的人工神经网络也是由一种基本的单元组成，不同的组成单元会使得人工神经网络表现能力各由不同，这里我们将介绍三种基本组成单元：感知器，线性单元和sigmoid单元，它们的结构都如下，唯一的不同在于这个输出函数（也称激励函数）是个什么类型的，下面我将简单的介绍下各个基本组成单元。

1.1感知器

    感知器是以实数值向量最为输入，计算这些输入的线性组合，若结果大于0，就为1，否则输出-1.函数形式如下

       这类感知器的表现能力是很有限的，它可以表示所有的原子布尔函数：与，或，与非和或非，但是却不能表示异或函数。比如说对于输入x1,x2现在感知器要输出他们与关系，它就可以表示出来，感知器有三个变量w0,w1,w2, f(x) = w0+w1*x1+w2*x2, 我可以让w0 = -0.8， w1 = w2 = 0.5,那么大姐可以分别对x1,x2取0和1看一下这个结果，比如x1 = 0,x2 = 1,那么F(x) = -0.8 + 0.5 *1 + 0.5 * 0 = -0.3, f(x) < 0 ,所以取0，结果正确，大家可以试着把其他三种情况带进去试一下。而异或关系它就没办法表示了，看下图：

你根本不可能划一根线把上面的0和1分开。

我们的目标就是通过样例训练基本单元，更新它们对应的权值，算法很简单：

for 所有的样例输入X

 更新每一个权重wi <---- wi + *wi

其中*wi  = a( t - 0 ) xi, t为样例的目标输出，而0是感知器的输出，a是一个小的常数叫学习速率。

这么简单的一个式子怎么就可以训练出正确的权值呢？

  为了有一个直观的理解，我举一个例子，若感知器正确分类，则 t - o为零，权值wi不

会调整；若目标输出为+1，而感知器输出为-1，也就是感知器低估了目标输出，此时

t - 0为 2，那么wi会增加 ； 反过来，若目标输出t为-1，感知器输出为+1，感知器高估

了目标的输出，此时t - o = -2，相应的wi就会减少。这样，通过有限次的使用感知器训

练法则，我们的权值向量就会收敛到一个能正确分类的权向量了，当然这个学习速度a

也要够小。

1.2 线性单元

线性单元和上面的感知器基本类似，也是f(x) =WX(注意大写为向量表示)，而它没有了这个阀值得判定，即f(n) = 1, ifWX > 0,这样它就比感知器要强大很多，当出现线性不可分的时候，感知器是毫无办法，没办法收敛,而线性单元会找到目标的最佳近似。它比感知器强大的地方在与它对问题空间的表示是连续的。

由于搜索空间为连续的，我们可以利用梯度下降来训练我们的权值W，其实现在的问题是我们能否找到一组权值W使得我们对样例的分类误差最小，那么我们应该怎样度量这个误差呢？

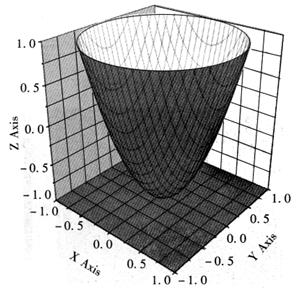
这里有一个很常用的度量方式E（W） = 1/2∑（t - d)^2 ,即所有样例的目标输出与线性单元输出之差平方的和最小。这是关于W的二次函数，大致图像可以表示成这样：

我们现在就是要找这个最小的那个点，在高中我们学过求抛物线的最小值，我们会进行求导，而这个梯度其实就是描述的是向量空间上的变化率。训练线性单元的梯度下降算法如下：

1.3sigmoid单元

线性单元的特点使的多个线性单元的组合产生的是一个线性函数，而如果我们想要表示非线性函数的网络时(现实生活中往往是非线性的)，就需要我们的非线性单元sigmoid单元，它和感知器非常的类似，图像如下：

其中x就是线性单元的输出。sigmoid函数有一个很好的性质就是它的导数很容易用它的输出表示：f'(x)=f(x)*[1-f(x)]，这个性质将再我们下面的反向传播算法中用到。

第二节 反向传播算法

对于有一系列确定的单元组成的多层网络，反向传播算法可用来学习这个网络的权值，它也是采用梯度下降的方法去最小化误差的平方。由于样例只对网络的输出提供了目标值，所以缺乏直接的目标值来计算隐藏单元的误差值，因此我们可通过如下方式计算：对受隐藏单元h影响的每个单元的误差进行加权求和，这样就刻化出了隐藏单元和输出值的关系。

这是针对只含一个隐秘层的算法：

其中上图的O代表的是sigmoid函数，t代表样例的目标输出。

反向传播算法实现了一种对可能的网络权值空间的梯度下降搜索，而对于多层网络来说，误差的曲面可能包含多个局部极小值（而不是像我们上图那样只有局部最小值就是全局最小值），反向传播算法只能保证收敛到局部最小值，但在现实应用中，人们发现局部最小值得问题并没有那么严重，你可以这样理解：网络的权越多（即维度越高），也就越为梯度下降提供更多的逃逸路线，让梯度下降离开相对该权值的局部最小值。