快速排序
快速排序是由C.A.R Hoare在1960年发明的,并被选为20世纪十大算法。在不要求稳定的应用场景中,快速排序是一种性能不错的、通用的排序算法。
在阅读完Robert Sedgewick的《算法》之后,尝试把几种快速排序整理在一起并总结。快速排序的精髓在于切分位置(Partition)的选取,本文希望把重点放在几种切分的区别上,淡化快速排序的原理和概念。本文所有源码来源于[1],都是从小到大排序。
0.快速排序两大实现方法
在《算法导论》中,快速排序有两种方法Hoare-Partition和Lomuto-Partition。简单的说,抛开中轴数(pivot)选取的不同不说,他们都有两个指针,Hoare的指针一头一尾,各往中间移动;Lomuto两个指针都是从前往后移动[4]。
Hoare-Partition(A, p, r)
x = A[p]
i = p - 1
j = r + 1
while true
repeat
j = j - 1
until A[j] <= x
repeat
i = i + 1
until A[i] >= x
if i < j
swap( A[i], A[j] )
else
return j
Lomuto-Partition(A, p, r)
x = A[r]
i = p - 1
for j = p to r - 1
if A[j] <= x
i = i + 1
swap( A[i], A[j] )
swap( A[i+1], A[r] )
return i + 11.Lomuto-Partition
QuickKR.java的实现参考了《The C Programming Language》一书,属于Lomuto方法。这是一种简单的快速排序实现,可以用在自己的小程序中,不适合用作对外发布库函数。对于某些特殊情况,它有继续优化的空间:[2,4]
- poor locality
应该是指局部访问性差,程序的重点在于内循环,即QuickKR.java的第28行,需要交换两个值,且下标last和i都是会变的,这样会造成CPU缓存命中率低 - 在特殊情况下,时间复杂度会恶化为O(n*n)
在元素都相同的情况下,切分会是lo(比较时无等号)或hi(比较时有等号);
在近似有序的情况下,切分会在lo附近。
切分最理想应该在lo和hi的中间,这样可达到O(nlogn)的复杂度。
//QuickKR.java
/****************************************************************************** * Compilation: javac QuickKR.java * Execution: java QuickKR N * Dependencies: StdIn.java StdOut.java * * Generate N random real numbers between 0 and 1 and quicksort them. * Uses version of quicksort from K+R. * * Reference: The C Programming Language by Brian W. Kernighan and * Dennis M. Ritchie, p. 87. * * Warning: goes quadratic if many duplicate keys. * ******************************************************************************/
public class QuickKR {
public static void sort(Comparable[] a) {
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
exch(a, lo, (lo + hi) / 2); // use middle element as partition
int last = lo;
for (int i = lo + 1; i <= hi; i++)
if (less(a[i], a[lo])) exch(a, ++last, i);
exch(a, lo, last);
sort(a, lo, last-1);
sort(a, last+1, hi);
}
/*************************************************************************** * Helper sorting functions. ***************************************************************************/
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
/*************************************************************************** * Check if array is sorted - useful for debugging. ***************************************************************************/
private static boolean isSorted(Comparable[] a) {
for (int i = 1; i < a.length; i++)
if (less(a[i], a[i-1])) return false;
return true;
}
// print array to standard output
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.println(a[i]);
}
}
/** * Reads in a sequence of strings from standard input; quicksorts them; * and prints them to standard output in ascending order. * Shuffles the array and then prints the strings again to * standard output, but this time, using the select method. */
public static void main(String[] args) {
String[] a = StdIn.readAllStrings();
QuickKR.sort(a);
show(a);
}
}2.0 Hoare-Partition
Quick.java是《算法》中的基本实现,属于Hoare方法,为什么说基本实现呢。因为后面的许多改进都是基于这个的。Quick.java(Hoare)优化了QuickKR.java(Lomuto)的局限性。
- 保持数据随机性
防止出现切分位置在头尾的情况 - 不跳过重复元素
Quick.java中有两个比较指针,一头一尾。在有重复元素的应用中,如果指针遇到跟比较元素相同的就跳过的话,会使得切分位置偏离中心点;如果遇到相同的就停下,虽然这样可能会不必要地将一些等值元素交换,但切分位置会被优化 - 内循环简洁
内循环(第73行至第78行)包含一个递增索引和固定值的比较,非常简洁,增大CPU缓存命中率
//Quick.java
/****************************************************************************** * Compilation: javac Quick.java * Execution: java Quick < input.txt * Dependencies: StdOut.java StdIn.java * Data files: http://algs4.cs.princeton.edu/23quicksort/tiny.txt * http://algs4.cs.princeton.edu/23quicksort/words3.txt * * Sorts a sequence of strings from standard input using quicksort. * * % more tiny.txt * S O R T E X A M P L E * * % java Quick < tiny.txt * A E E L M O P R S T X [ one string per line ] * * % more words3.txt * bed bug dad yes zoo ... all bad yet * * % java Quick < words3.txt * all bad bed bug dad ... yes yet zoo [ one string per line ] * * * Remark: For a type-safe version that uses static generics, see * * http://algs4.cs.princeton.edu/23quicksort/QuickPedantic.java * ******************************************************************************/
/** * The <tt>Quick</tt> class provides static methods for sorting an * array and selecting the ith smallest element in an array using quicksort. * <p> * For additional documentation, see <a href="http://algs4.cs.princeton.edu/21elementary">Section 2.1</a> of * <i>Algorithms, 4th Edition</i> by Robert Sedgewick and Kevin Wayne. * * @author Robert Sedgewick * @author Kevin Wayne */
public class Quick {
// This class should not be instantiated.
private Quick() { }
/** * Rearranges the array in ascending order, using the natural order. * @param a the array to be sorted */
public static void sort(Comparable[] a) {
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
assert isSorted(a);
}
// quicksort the subarray from a[lo] to a[hi]
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
assert isSorted(a, lo, hi);
}
// partition the subarray a[lo..hi] so that a[lo..j-1] <= a[j] <= a[j+1..hi]
// and return the index j.
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo;
int j = hi + 1;
Comparable v = a[lo];
while (true) {
// find item on lo to swap
while (less(a[++i], v))
if (i == hi) break;
// find item on hi to swap
while (less(v, a[--j]))
if (j == lo) break; // redundant since a[lo] acts as sentinel
// check if pointers cross
if (i >= j) break;
exch(a, i, j);
}
// put partitioning item v at a[j]
exch(a, lo, j);
// now, a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
return j;
}
/** * Rearranges the array so that a[k] contains the kth smallest key; * a[0] through a[k-1] are less than (or equal to) a[k]; and * a[k+1] through a[N-1] are greater than (or equal to) a[k]. * @param a the array * @param k find the kth smallest */
public static Comparable select(Comparable[] a, int k) {
if (k < 0 || k >= a.length) {
throw new IndexOutOfBoundsException("Selected element out of bounds");
}
StdRandom.shuffle(a);
int lo = 0, hi = a.length - 1;
while (hi > lo) {
int i = partition(a, lo, hi);
if (i > k) hi = i - 1;
else if (i < k) lo = i + 1;
else return a[i];
}
return a[lo];
}
/*************************************************************************** * Helper sorting functions. ***************************************************************************/
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
/*************************************************************************** * Check if array is sorted - useful for debugging. ***************************************************************************/
private static boolean isSorted(Comparable[] a) {
return isSorted(a, 0, a.length - 1);
}
private static boolean isSorted(Comparable[] a, int lo, int hi) {
for (int i = lo + 1; i <= hi; i++)
if (less(a[i], a[i-1])) return false;
return true;
}
// print array to standard output
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.println(a[i]);
}
}
/** * Reads in a sequence of strings from standard input; quicksorts them; * and prints them to standard output in ascending order. * Shuffles the array and then prints the strings again to * standard output, but this time, using the select method. */
public static void main(String[] args) {
String[] a = StdIn.readAllStrings();
Quick.sort(a);
show(a);
// shuffle
StdRandom.shuffle(a);
// display results again using select
StdOut.println();
for (int i = 0; i < a.length; i++) {
String ith = (String) Quick.select(a, i);
StdOut.println(ith);
}
}
}2.1 对Quick.java的改进
- 用哨兵取消边界测试
左哨兵:第78行其实可以直接省略,因为有a[lo]作为左边的哨兵,在lo必定会停下;右哨兵:在第一次切分数组前,将最大的元素放置于a[length-1],在后续子问题的切分中,可将右数组的最左元素作为左数组的右哨兵。 - 小规模数组切换至插入排序
对于小数组,快速排序比插入排序慢,M可取5~15
if(hi<= lo + M){
Insertion.sort(a, lo, hi);
return;
}- 三取样切分(Median-of-three partitioning)
目前的切分元素是随机选择的,三取样希望选取小范围里的中位数。在QuickX.java(在[1]中有完整代码)中,当排序元素<=40时,选取前中后三个元素的中位数;当N较大时,使用Tukey ninther法[],9个候选元素等间隔排开,然后得出前段中位数m1,中段中位数m2,后段中位数m3,再计算m1-3的中位数。这里要注意,Tukey ninther方法计算出的中位数并不是9个等间隔候选元素的中位数。
// use median-of-3 as partitioning element
else if (N <= 40) {
int m = median3(a, lo, lo + N/2, hi);
exch(a, m, lo);
}
// use Tukey ninther as partitioning element
else {
int eps = N/8;
int mid = lo + N/2;
int m1 = median3(a, lo, lo + eps, lo + eps + eps);
int m2 = median3(a, mid - eps, mid, mid + eps);
int m3 = median3(a, hi - eps - eps, hi - eps, hi);
int ninther = median3(a, m1, m2, m3);
exch(a, ninther, lo);
}- 三向切分(three-way partitioning)
3-way partitioning最早是由Dijkstra(就是最短路径那个人)在1976年的《A Discipline of Programming》一书出提出,当时提出这个算法是为了解决“荷兰国旗问题”,又由于快速排序中的partitioning步骤非常像荷兰国旗问题中的步骤,于是就将荷兰国旗问题中的partitioning用到快速排序中[5,8]。
在实践中,Dijkstra的方法很少使用,因为在没有相等元素的情况下,Dijkstra对于每个元素都要进行交换,且其子问题的规模并没有比父问题小很多,其交换次数要3倍于优化过的2路的Quick.java[4,5]。那在实践中,用的是哪个算法呢。在C++ standard library和Java 6 runtime library中,sort函数使用的是”fat partitioning”,这个方法由Bentley和Mcllroy提出[6]。在有较多重复值时,Bentley-McIlroy的方法比Dijkstra多了交换的步骤(第40~43行);在无重复值的情况下,Bentley-McIlroy方法相较于2路的Quick.java,由于头尾只有少量的等值元素需要交换,所以额外的开销很小。因此,Bentley-McIlroy更适合作为库函数,因为我们不能去预测用户的数据是怎么样的。

// Dijkstra 3-way partitioning 上述左图
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int lt = lo, gt = hi;
Comparable v = a[lo];
int i = lo+1;
while (i <= gt)
{
int cmp = a[i].compareTo(v);
if (cmp < 0) exch(a, lt++, i++);
else if (cmp > 0) exch(a, i, gt--);
else i++;
}
sort(a, lo, lt - 1);
sort(a, gt + 1, hi);
}
// Bentley-McIlroy 3-way partitioning 上述右图
private static void sort(Comparable[] a, int lo, int hi) {
int i = lo, j = hi+1;
int p = lo, q = hi+1;
Comparable v = a[lo];
while (true) {
while (less(a[++i], v))
if (i == hi) break;
while (less(v, a[--j]))
if (j == lo) break;
// pointers cross
if (i == j && eq(a[i], v))
exch(a, ++p, i);
if (i >= j) break;
exch(a, i, j);
if (eq(a[i], v)) exch(a, ++p, i);
if (eq(a[j], v)) exch(a, --q, j);
}
i = j + 1;
for (int k = lo; k <= p; k++)
exch(a, k, j--);
for (int k = hi; k >= q; k--)
exch(a, k, i++);
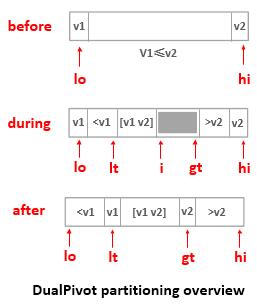
}2.2 Dual-Pivot Quicksort
在Java 7 runtime library中,使用的是Dual-Pivot Quicksort[7],有两个中轴数,由Vladimir Yaroslavskiy等人提出。
3 .趣味应用
Bentley and McIlroy的三路切分的快速排序在Java库中工作的不错,即使输入的数据是近似有序的。M. D. MCILROY在1999年的一篇论文中提出一种方法[9],可以产生一组数据,使得快速排序的性能恶化到最差,这个方法被叫做killer adversary(快速排序的无敌对手)。64点的最差输入如下:
G. J. E. Rawlins在《Compared to what? an introduction to the analysis of algorithms》(1991年)这本书上提出了一个螺帽和螺钉的配对问题:有N个螺钉和N个螺帽,一个螺帽只能和一个螺钉配对,一个螺钉也只能和一个螺帽配对。现在只能任意去配对一组,然后去观察哪个比较大(若螺帽大,套在螺钉上就显得松;若螺钉大,就钻不进螺帽),但是不能直接比较两个螺帽或两个螺钉,有没有有效的解决方法?[10]
【Reference】
[1]《Algorithms》4th Edition http://algs4.cs.princeton.edu/23quicksort
[2]快速排序性能可视化 http://www.sorting-algorithms.com/quick-sort
[3]Tukey ninther方法 http://www.johndcook.com/blog/2009/06/23/tukey-median-ninther/
[4]Quicksort Partitioning: Hoare vs. Lomuto http://cs.stackexchange.com/questions/11458/quicksort-partitioning-hoare-vs-lomuto/11550#11550
[5]QuickSort Dijkstra 3-Way Partitioning: why the extra swapping? http://cs.stackexchange.com/questions/22389/quicksort-dijkstra-3-way-partitioning-why-the-extra-swapping
[6]fat partitioning http://pauillac.inria.fr/~maranget/X/421/09/bentley93engineering.pdf
[7]Java 7 runtime library http://docs.oracle.com/javase/7/docs/api/java/util/Arrays.html#sort%28int%5B%5D%29
[8]台湾中央研究院,穆信成 http://www.iis.sinica.edu.tw/~scm/ncs/2010/10/dutch-national-flag-problem/
[9]A Killer Adversary for Quicksort http://www.cs.dartmouth.edu/~doug/mdmspe.pdf
[10]Matching Nuts and Bolts - Solution http://www.wisdom.weizmann.ac.il/~naor/PUZZLES/nuts_solution.html
20世纪十大算法:http://www.uta.edu/faculty/rcli/TopTen/topten.pdf
浅谈算法和数据结构: 四 快速排序http://www.cnblogs.com/yangecnu/p/Introduce-Quick-Sort.html
QuicksortIsOptimal,作者:Robert Sedgewick,Jon Bentley http://www.sorting-algorithms.com/static/QuicksortIsOptimal.pdf
