编写C语言版本的卷积神经网络CNN之二：CNN网络的总体结构

原创文章

转载请注册来源 http://blog.csdn.net/tostq

      上一节我们总体介绍项目并说明Minst手写数字数据库的使用，这一节我们将重点介绍CNN网络总体结构。

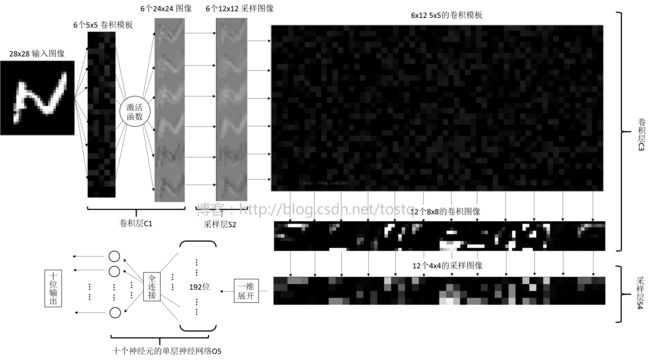
      上图我们已经非常熟悉，其为Yann在1998年介绍的LeNet-5网络的结构，其刚被提出，就在学术和工业领域上得到广泛应用，而本文的CNN卷积网络却是如下图所示（博主自己画的，画这个图还是挺麻烦的：L，不清晰请原谅），和LeNet-5相比主要有以下三点不同：

      （1）LeNet-5给输入图像增加了一圈黑边，使输入图像大小变成了32x32，这样的目的是为了在下层卷积过程中保留更多原图的信息。

      （2）LeNet-5的卷积层C3只有16个模板，得到16个输出，而本文的卷积层C3由于是全连接，所以有6*12个模板，得到12个输出图像

      （3）LeNet-5多了两种，分别是C5到F6的全连接神经网络层，和F6到OUTPUT高斯连接网络层。而本文的直接由采样层S4直接经过一层全连接神经网络层到OUTPUT。

      下面我们将重点介绍各层的结构及数据的前向传播。

一、各层的解释

（1） 卷积层C1

      输入为28x28的灰度图像，灰度图像分别同6个5x5的模板进行卷积操作，分别得到了6个24x24的卷积图像，图像里的每个像素加上一个权重，并经过一个激活函数，得到该层的输出。

      所以该层的相关参数为：6个5x5的模板参数w，6个模板对应的权重参数b，共6x5x5+6个参数

Tips:

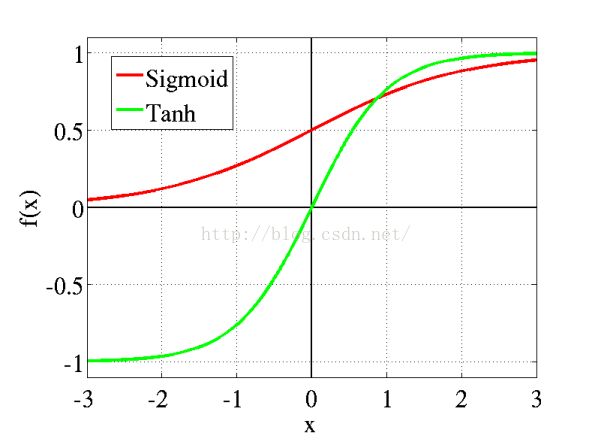
      关于激活函数：激活函数我们在学习神经网络时就已经接触过了，其主要有两个目的，第一是将数据钳制在一定范围内（如Sigmoid函数将数据压缩在-1到1之间），不太高也不太低，第二是用来加入非线性因素的，因为线性模型的表达能力不够。传统神经网络中最常用的两个激活函数Sigmoid系和Tanh系，而Sigmoid系（Logistic-Sigmoid、Tanh-Sigmoid）被视为神经网络的核心所在。本文的例子就是Sigmoid系。

      近年来，在深度学习领域中效果最好，应用更为广泛的是ReLu激活函数，其相较于Sigmoid系，主要变化有三点：①单侧抑制 ②相对宽阔的兴奋边界 ③稀疏激活性。特别是在神经科学方面，除了新的激活频率函数之外，神经科学家还发现了的稀疏激活性广泛存在于大脑的神经元， 神经元编码工作方式具有稀疏性和分布性。 大脑同时被激活的神经元只有1~4%。  从信号方面来看，即神经元同时只对输入信号的少部分选择性响应，大量信号被刻意的屏蔽了，这样可以提高学习的精度，更好更快地提取稀疏特征。而 在经验规则的初始化W之后，传统的Sigmoid系函数同时近乎有一半的神经元被激活，这不符合神经科学的研究，而且会给深度网络训练带来巨大问题。 Softplus照顾到了新模型的前两点，却没有稀疏激活性。因而，校正函数max(0,x)即ReLu函数成了最大赢家。

（2）采样层S2及S4（Pooling层）

      采样层S又名Pooling层，Pooling主要是为了减少数据处理的维度，常见的pooling方法有max pooling和average pooling等。

       max pooling 就是选择当前块内最大像素值来表示当前局部块

       average pooling 就是选择当前块的像素值平均值来代替

      本文的选择Pooling方法是average pooling，而使用广泛效果较好的方法却是max pooling。（看到这里，你可能会吐槽，为什么不用效果好，因为平均计算相比而言，有那么一丢丢简单！）

（3） 卷积层C3

      这里的卷积层是一个全连接的卷积层。输出的卷积公式如下，这里I表示图像，W表示卷积模板，b表示偏重，φ表示激活函数，i表示输入图像序号（i=1~6），j表示该层输出图像序号（j=1~12）

      由此可以看到在卷积层C3中输入为6个12x12的图像，输出为12个8x8的图像

      所需要训练的参数有6x12个5x5的卷积模板w和12个偏重b（每个模板对应的偏重都是相同的）

      而实际上由于神经网络的稀疏结构和减少训练时间的需要，该卷积层一般不是利用全连接的，就比如前面介绍LeNet-5网络，只需要利用16个卷积模板就可以了，而不是全连接的6x12个，其连接方法如下，其最终得到16个输出图像。

      这里X表示选择卷积，比如第0张输出图像是由第0、1、2张输入图像分别同第0个卷积模板卷积相加，再加上偏重，经过激活函数得到的。而第15张图像是由第0、1、2、3、4、5张输入图像分别同第15个卷积模板卷积相加得到的。

（4）输出层O5：

      采样层S4后，我们将得到12张4*4的图像，将所有图像展开成一维，就得到了12*4*4=192位的向量。

输出层是由输入192位，输出10位的全连接单层神经网络，共有10个神经元构成，每个神经元都同192位输入相连，即都有192位的输入和1位输出，其处理公式如下，这里j表示输出神经元的序号，i表示输入的序号。

      所以该层参数共有192*10个权重w，和10个偏重b

二、卷积神经网络的相关数据结构

      这个卷积网络主要有五层网络，主要结构是卷积层、采样层（Pooling）、卷积层、采样层（Pooling）和全连接的单层神经网络层（输出层），所以我们建立了三个基本层的结构及一个总的卷积网络结构。

      这里结构内除了必要的权重参数，而需要记录该层输入输出数据y，及需要传递到下一层的局部梯度d。

（1）卷积层

// 卷积层
typedef struct convolutional_layer{
    int inputWidth;   //输入图像的宽
    int inputHeight;  //输入图像的长
    int mapSize;      //特征模板的大小，模板一般都是正方形

    int inChannels;   //输入图像的数目
    int outChannels;  //输出图像的数目

    // 关于特征模板的权重分布，这里是一个四维数组
    // 其大小为inChannels*outChannels*mapSize*mapSize大小
    // 这里用四维数组，主要是为了表现全连接的形式，实际上卷积层并没有用到全连接的形式
    // 这里的例子是DeapLearningToolboox里的CNN例子，其用到就是全连接
    float**** mapData;     //存放特征模块的数据
    float**** dmapData;    //存放特征模块的数据的局部梯度

    float* basicData;   //偏置，偏置的大小，为outChannels
    bool isFullConnect; //是否为全连接
    bool* connectModel; //连接模式（默认为全连接）

    // 下面三者的大小同输出的维度相同
    float*** v; // 进入激活函数的输入值
    float*** y; // 激活函数后神经元的输出

    // 输出像素的局部梯度
    float*** d; // 网络的局部梯度,δ值  
}CovLayer;

（2）采样层

// 采样层 pooling
typedef struct pooling_layer{
    int inputWidth;   //输入图像的宽
    int inputHeight;  //输入图像的长
    int mapSize;      //特征模板的大小

    int inChannels;   //输入图像的数目
    int outChannels;  //输出图像的数目

    int poolType;     //Pooling的方法
    float* basicData;   //偏置

    float*** y; // 采样函数后神经元的输出,无激活函数
    float*** d; // 网络的局部梯度,δ值
}PoolLayer;

（3）全连接的单层神经网络

// 输出层 全连接的神经网络
typedef struct nn_layer{
    int inputNum;   //输入数据的数目
    int outputNum;  //输出数据的数目

    float** wData; // 权重数据，为一个inputNum*outputNum大小
    float* basicData;   //偏置，大小为outputNum大小

    // 下面三者的大小同输出的维度相同
    float* v; // 进入激活函数的输入值
    float* y; // 激活函数后神经元的输出
    float* d; // 网络的局部梯度,δ值

    bool isFullConnect; //是否为全连接
}OutLayer;

（4）各层共同组成一个完整的卷积网络

typedef struct cnn_network{
    int layerNum;
    CovLayer* C1;
    PoolLayer* S2;
    CovLayer* C3;
    PoolLayer* S4;
    OutLayer* O5;

    float* e; // 训练误差
    float* L; // 瞬时误差能量
}CNN;

（5） 另外还有一个用于存放训练参量的结构

typedef struct train_opts{
    int numepochs; // 训练的迭代次数
    float alpha; // 学习速率
}CNNOpts;

三、卷积神经网络的初始化

       卷积神经网络的初始化主要包含了各数据的 空间 初始化及权重的随机赋值，没有什么复杂，按照结构分配空间就可以了，这里不再详细赘述了，可以直接参考代码内cnnsetup()函数

四、卷积神经网络的前向传播过程

       前向传播过程实际上就是指输入图像数据，得到输出结果的过程，而后向传播过程就是将输出结果的误差由后向前传递给各层，各层依次调整权重的过程。所以前向传播过程相比而是比较直观，而且简单的。

前向传播过程在项目中主要是由cnnff函数完成，下面我们将按层介绍其过程

（1）卷积层C1

       卷积层C1共有6个卷积模板，每个模板同输入图像卷积将会得到一个输出，即共6个输出，以下是图像的卷积公式：

       C1层的相关代码，这里cov函数是卷积函数，在mat.cpp是具体的定义，activation_Sigma是激活函数

    int outSizeW=cnn->S2->inputWidth;
    int outSizeH=cnn->S2->inputHeight;
    // 第一层的传播
    int i,j,r,c;
    // 第一层输出数据
    nSize mapSize={cnn->C1->mapSize,cnn->C1->mapSize};
    nSize inSize={cnn->C1->inputWidth,cnn->C1->inputHeight};
    nSize outSize={cnn->S2->inputWidth,cnn->S2->inputHeight};
    for(i=0;i<(cnn->C1->outChannels);i++){
        for(j=0;j<(cnn->C1->inChannels);j++){
            float** mapout=cov(cnn->C1->mapData[j][i],mapSize,inputData,inSize,valid);
            addmat(cnn->C1->v[i],cnn->C1->v[i],outSize,mapout,outSize);
            for(r=0;r<outSize.r;r++)
                free(mapout[r]);
            free(mapout);
        }
        for(r=0;r<outSize.r;r++)
            for(c=0;c<outSize.c;c++)
                cnn->C1->y[i][r][c]=activation_Sigma(cnn->C1->v[i][r][c],cnn->C1->basicData[i]);
    }

（2）采样层S2，avgPooling是平均Pooling函数

   

 // 第二层的输出传播S2，采样层
    outSize.c=cnn->C3->inputWidth;
    outSize.r=cnn->C3->inputHeight;
    inSize.c=cnn->S2->inputWidth;
    inSize.r=cnn->S2->inputHeight;
    for(i=0;i<(cnn->S2->outChannels);i++){
        if(cnn->S2->poolType==AvePool)
            avgPooling(cnn->S2->y[i],outSize,cnn->C1->y[i],inSize,cnn->S2->mapSize);
    }

（3）卷积层C3，同C1很类似    

// 第三层输出传播,这里是全连接
    outSize.c=cnn->S4->inputWidth;
    outSize.r=cnn->S4->inputHeight;
    inSize.c=cnn->C3->inputWidth;
    inSize.r=cnn->C3->inputHeight;
    mapSize.c=cnn->C3->mapSize;
    mapSize.r=cnn->C3->mapSize;
    for(i=0;i<(cnn->C3->outChannels);i++){
        for(j=0;j<(cnn->C3->inChannels);j++){
            float** mapout=cov(cnn->C3->mapData[j][i],mapSize,cnn->S2->y[j],inSize,valid);
            addmat(cnn->C3->v[i],cnn->C3->v[i],outSize,mapout,outSize);
            for(r=0;r<outSize.r;r++)
                free(mapout[r]);
            free(mapout);
        }
        for(r=0;r<outSize.r;r++)
            for(c=0;c<outSize.c;c++)
                cnn->C3->y[i][r][c]=activation_Sigma(cnn->C3->v[i][r][c],cnn->C3->basicData[i]);
    }

（4）采样层S4，同S2很类似  

// 第四层的输出传播
    inSize.c=cnn->S4->inputWidth;
    inSize.r=cnn->S4->inputHeight;
    outSize.c=inSize.c/cnn->S4->mapSize;
    outSize.r=inSize.r/cnn->S4->mapSize;
    for(i=0;i<(cnn->S4->outChannels);i++){
        if(cnn->S4->poolType==AvePool)
            avgPooling(cnn->S4->y[i],outSize,cnn->C3->y[i],inSize,cnn->S4->mapSize);
    }

（5）输出层O5

    // 输出层O5的处理
    // 首先需要将前面的多维输出展开成一维向量
    float* O5inData=(float*)malloc((cnn->O5->inputNum)*sizeof(float)); 
    for(i=0;i<(cnn->S4->outChannels);i++)
        for(r=0;r<outSize.r;r++)
            for(c=0;c<outSize.c;c++)
                O5inData[i*outSize.r*outSize.c+r*outSize.c+c]=cnn->S4->y[i][r][c];

    nSize nnSize={cnn->O5->inputNum,cnn->O5->outputNum};
    nnff(cnn->O5->v,O5inData,cnn->O5->wData,cnn->O5->basicData,nnSize);
    for(i=0;i<cnn->O5->outputNum;i++)
        cnn->O5->y[i]=activation_Sigma(cnn->O5->v[i],cnn->O5->basicData[i]);
    free(O5inData);
}

 项目代码地址： https://github.com/tostq/DeepLearningC/tree/master/CNN