Theano-Deep Learning Tutorials 笔记:Convolutional Neural Networks (LeNet)
教程地址：http://www.deeplearning.net/tutorial/lenet.html
Motivation
Convolutional Neural Networks（卷积神经网络）是受动物视觉系统启发而设计的，本节主要讲解了LeNet-5 [LeCun98]这个网络结构的实现，当时美国许多银行使用这个系统来进行手写支票的识别。
卷积神经网络的详细介绍可以看：http://blog.csdn.net/zouxy09/article/details/8781543
Sparse Connectivity
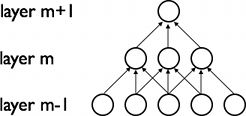
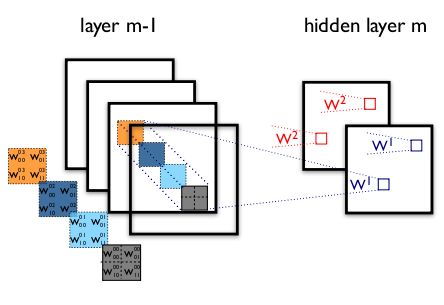
局部连接（局部感受野）：某层神经元，只与前一层部分神经元相连（这是受动物视觉系统启发，某些神经细胞只负责接收部分区域的信息），如图，m层最左神经元只与m-1层左边3个神经元相连，而第4个与它距离较远，不属于它的管辖范围，所以不需要连接。
注意：随着层数越来越多，信息处理也越来越却与全局信息：如第二层神经元只接受处理（第一层）3个神经元的信息，而第三层神经元接受了（第一层）5个神经元的信息（信息更全局化了）
Shared Weights
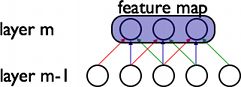
权值（参数）共享：图中红、蓝、绿颜色相同的连接就代表了共享的参数，过程类似图像处理中的空间滤波模板（核），一个模板（模板中的参数共享）与图像卷积（在图像上滑动提取特征）得到一个feature map，这些特征和具体在图像中的位置无关，就是说图像中哪里都可能有这些特征。
权值共享大大减少了参数数量，提高了CNN在视觉问题上的泛化能力（参数少了，模型更简单了，更不容易过拟合了）。
Details and Notation
注意：每个feature map对应一个filter，filter可以理解为卷积核，类似图像处理中各种空间滤波的(3*3，8*8)的模板。
我的另一篇UFLDL教程答案(8):Exercise:Convolution and Pooling里也有说明。
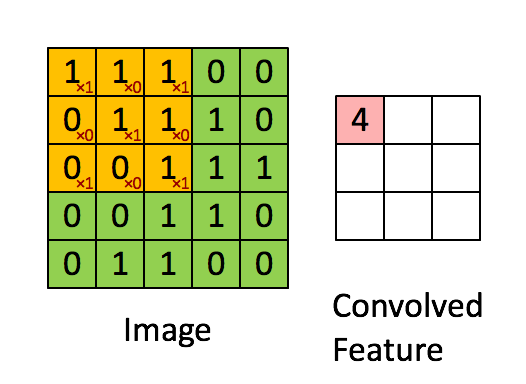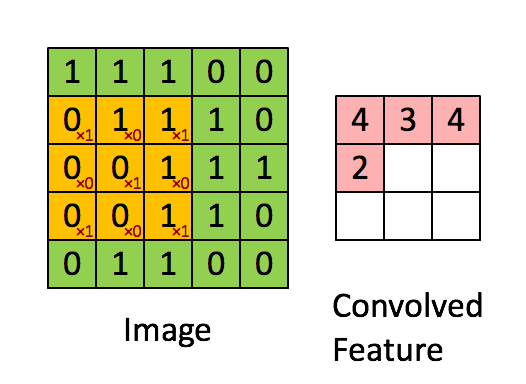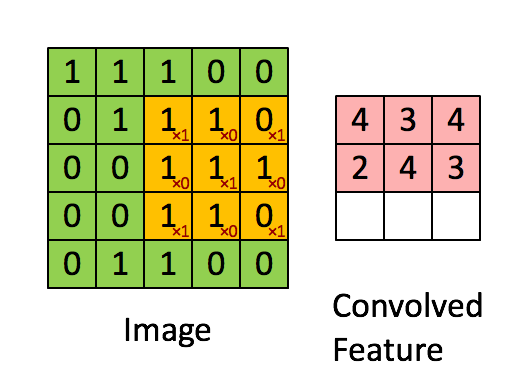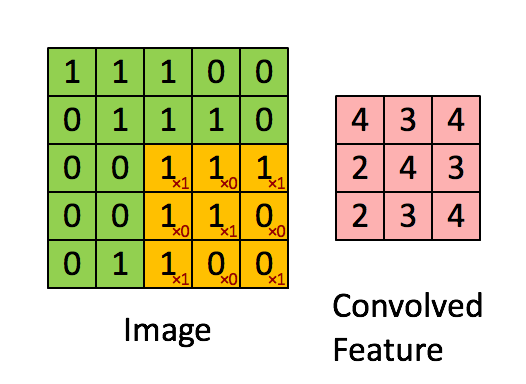
绿色为原图，黄色为filter(卷积核)，粉红色为feature map。当然，图中情况激活函数不是tanh而是直接等于，而且偏置b也为0。但是上图说明了为啥叫卷积神经网络。
If we denote the k-th feature map at a given layer as
, whosefilters are determined by the weights 
and bias
, then the feature map is obtained as follows (for non-linearities):
* 表示卷积：![o[m,n] = f[m,n]*g[m,n] = \sum_{u=-\infty}^{\infty} \sum_{v=-\infty}^{\infty} f[u,v] g[m-u,n-v]](http://img.e-com-net.com/image/info5/fe30bb7e1917414787222b7ba9a514d2.png){kind=small}
，就是上面GIF图那样。
每个隐层都有许多个feature map，，每层的参数 W 是一个4维张量（本层第几个feature map，前一层第几个feature map，前一层多少行，前一层多少列）。参数 b 是一个向量，有多少个feature map 就多少维。
注意观察图中，w的4维序号：
denotes the weight connecting each pixel of thek-th feature mapat layer m, with the pixel atcoordinates (i,j) of thel-th feature map of layer (m-1).
The Convolution Operator
有Theano，卷积很容易实现：使用 theano.tensor.signal.conv2d 即可，输入为2个4维张量（这里说成4维数组更好，说成张量确实不准确，但是tensor翻译确实是张量）：
a 4D tensor corresponding to a mini-batch of input images：（mini-batch size, number of input feature maps, image height, image width）
a 4D tensor corresponding to the weight matrix ：（number of feature maps at layer m, number of feature maps at layer m-1, filter height, filter width）
本例输入为120*160的RGB3通道图像（即3个feature map），filter 为 9*9 。
import theano
from theano import tensor as T
from theano.tensor.nnet import conv
import numpy
rng = numpy.random.RandomState(23455)
# instantiate 4D tensor for input
input = T.tensor4(name='input')
# initialize shared variable for weights.
w_shp = (2, 3, 9, 9)
w_bound = numpy.sqrt(3 * 9 * 9)
W = theano.shared( numpy.asarray(
rng.uniform(
low=-1.0 / w_bound,
high=1.0 / w_bound,
size=w_shp),
dtype=input.dtype), name ='W')
# initialize shared variable for bias (1D tensor) with random values
# IMPORTANT: biases are usually initialized to zero. However in this
# particular application, we simply apply the convolutional layer to
# an image without learning the parameters. We therefore initialize
# them to random values to "simulate" learning.
b_shp = (2,)
b = theano.shared(numpy.asarray(
rng.uniform(low=-.5, high=.5, size=b_shp),
dtype=input.dtype), name ='b')
# build symbolic expression that computes the convolution of input with filters in w
conv_out = conv.conv2d(input, W)
# build symbolic expression to add bias and apply activation function, i.e. produce neural net layer output
# A few words on ``dimshuffle`` :
# ``dimshuffle`` is a powerful tool in reshaping a tensor;
# what it allows you to do is to shuffle dimension around
# but also to insert new ones along which the tensor will be
# broadcastable;
# dimshuffle('x', 2, 'x', 0, 1)
# This will work on 3d tensors with no broadcastable
# dimensions. The first dimension will be broadcastable,
# then we will have the third dimension of the input tensor as
# the second of the resulting tensor, etc. If the tensor has
# shape (20, 30, 40), the resulting tensor will have dimensions
# (1, 40, 1, 20, 30). (AxBxC tensor is mapped to 1xCx1xAxB tensor)
# More examples:
# dimshuffle('x') -> make a 0d (scalar) into a 1d vector
# dimshuffle(0, 1) -> identity
# dimshuffle(1, 0) -> inverts the first and second dimensions
# dimshuffle('x', 0) -> make a row out of a 1d vector (N to 1xN)
# dimshuffle(0, 'x') -> make a column out of a 1d vector (N to Nx1)
# dimshuffle(2, 0, 1) -> AxBxC to CxAxB
# dimshuffle(0, 'x', 1) -> AxB to Ax1xB
# dimshuffle(1, 'x', 0) -> AxB to Bx1xA
output = T.nnet.sigmoid(conv_out + b.dimshuffle('x', 0, 'x', 'x'))
# create theano function to compute filtered images
f = theano.function([input], output)
注释详细解释了，dimshuffle 函数，此函数的使用主要是让 b 的维度与 conv_out 一致，即与 input 维度一致 [mini-batch size, number of input feature maps, image height, image width]。b本来为2维向量，b.dimshuffle('x', 0, 'x', 'x'))，把2维调整到了 0 那里，对应上了 number of input feature maps。感觉这个好难用语言解释。。。
权重初值：
依然是均匀分布随机抽样，[-1/fan-in, 1/fan-in]，fan-in 是一个隐藏层神经元的输入数量（feature map数 * filter权重个数=3*9*9）；多层感知器里是使用的前一层所有神经元个数，但CNN中就得考虑 the number of input feature maps（3） and the size of the receptive fields（9*9）。
做一个小实验：
import numpy
import pylab
from PIL import Image
# open random image of dimensions 639x516
img = Image.open(open('doc/images/3wolfmoon.jpg'))
# dimensions are (height, width, channel)
img = numpy.asarray(img, dtype='float64') / 256.
# put image in 4D tensor of shape (1, 3, height, width)
img_ = img.transpose(2, 0, 1).reshape(1, 3, 639, 516)
filtered_img = f(img_)
# plot original image and first and second components of output
pylab.subplot(1, 3, 1); pylab.axis('off'); pylab.imshow(img)
pylab.gray();
# recall that the convOp output (filtered image) is actually a "minibatch",
# of size 1 here, so we take index 0 in the first dimension:
pylab.subplot(1, 3, 2); pylab.axis('off'); pylab.imshow(filtered_img[0, 0, :, :])
pylab.subplot(1, 3, 3); pylab.axis('off'); pylab.imshow(filtered_img[0, 1, :, :])
pylab.show()
结果：随机取的权重却得到了边缘检测器般的效果！
MaxPooling
最大值池化（也有平均值池化）：把图片分为几个块，每个块缩为一个像素，像素值取块中像素的最大值。
Another important concept of CNNs is max-pooling, which is a form ofnon-linear down-sampling. Max-pooling partitions the input image into a set ofnon-overlapping rectangles and, for each such sub-region, outputs the maximum value.
池化的原因：
（1）减少像素数量，使后续网络层的计算简化。
（2）池化使CNN有了变换不变性，由于池化取了块内的最大值，如果图像出现不太明显的平移和旋转，这个最大值是不变的，这也就实现了变换不变性。
使用函数 theano.tensor.signal.downsample.max_pool_2d 实现池化，输入为 N dimensional tensor (where N >= 2)，performs max-pooling overthe 2 trailing dimensions of the tensor。
池化的例子：
from theano.tensor.signal import downsample
input = T.dtensor4('input')
maxpool_shape = (2, 2)
pool_out = downsample.max_pool_2d(input, maxpool_shape, ignore_border=True)
f = theano.function([input],pool_out)
invals = numpy.random.RandomState(1).rand(3, 2, 5, 5)
print 'With ignore_border set to True:'
print 'invals[0, 0, :, :] =\n', invals[0, 0, :, :]
print 'output[0, 0, :, :] =\n', f(invals)[0, 0, :, :]
pool_out = downsample.max_pool_2d(input, maxpool_shape, ignore_border=False)
f = theano.function([input],pool_out)
print 'With ignore_border set to False:'
print 'invals[1, 0, :, :] =\n ', invals[1, 0, :, :]
print 'output[1, 0, :, :] =\n ', f(invals)[1, 0, :, :]
结果如下：
With ignore_border set to True:
invals[0, 0, :, :] =
[[ 4.17022005e-01 7.20324493e-01 1.14374817e-04 3.02332573e-01 1.46755891e-01]
[ 9.23385948e-02 1.86260211e-01 3.45560727e-01 3.96767474e-01 5.38816734e-01]
[ 4.19194514e-01 6.85219500e-01 2.04452250e-01 8.78117436e-01 2.73875932e-02]
[ 6.70467510e-01 4.17304802e-01 5.58689828e-01 1.40386939e-01 1.98101489e-01]
[ 8.00744569e-01 9.68261576e-01 3.13424178e-01 6.92322616e-01 8.76389152e-01]]
output[0, 0, :, :] =
[[ 0.72032449 0.39676747]
[ 0.6852195 0.87811744]]
With ignore_border set to False:
invals[1, 0, :, :] =
[[ 0.01936696 0.67883553 0.21162812 0.26554666 0.49157316]
[ 0.05336255 0.57411761 0.14672857 0.58930554 0.69975836]
[ 0.10233443 0.41405599 0.69440016 0.41417927 0.04995346]
[ 0.53589641 0.66379465 0.51488911 0.94459476 0.58655504]
[ 0.90340192 0.1374747 0.13927635 0.80739129 0.39767684]]
output[1, 0, :, :] =
[[ 0.67883553 0.58930554 0.69975836]
[ 0.66379465 0.94459476 0.58655504]
[ 0.90340192 0.80739129 0.39767684]]
注意，ignore_border 为 true，false 的功能。
The Full Model: LeNet
前面几层使用的4D tensors，到后面需要转成2D matrix，以便与之前实现的多层感知器兼容。
卷积可以通过下面几种方式实现：
- theano.tensor.nnet.conv2d, which is the most common one in almost all of the recent published convolutional models. In this operation, each output feature map is connected to each input feature map by a different 2D filter, and its value isthe sum of the individual convolution of all inputs through the corresponding filter.
- The convolution used in the original LeNet model: In this work, each output feature map isonly connected to a subset of input feature maps.
- The convolution used in signal processing: theano.tensor.signal.conv.conv2d, which works only on single channel inputs.
这里，我用使用的是第一种，连接前一层的所有feature map，而不是连接部分feature map（第二种是连接部分）。
最初LeNet使用第二种方式的原因：1.减少计算量，但现在计算机性能已经明显提高了，不需要这样了；2.slightly reduce the number of free parameters，这一点的意思是减少自由参数，防止过拟合，但我们可以用其他正则化方法来防止过拟合。
Putting it All Together
具体看教程，有可下载的完整代码，使用到了前几节的代码
网络使用的随机初值，并没有像UFLDL那样用自编码器逐层训练卷积层权值；也没有体现反向传导，而是用的Theano黑科技对每层参数直接求导，然后梯度下降更新参数。错误率只有 0.930000 % ，比UFLDL的两层自编码加一层softmax（正确率为97.74%）性能差一些。
Tips and Tricks
Choosing Hyperparameters
CNN的hyper-parameters比MLP更多，之前在MLP中提到的learning rates and regularization constants依然适用。下面介绍CNN特有的各种参数选择：
Number of filters（等于feature map的数量）
Assume layer 
contains feature maps and
pixel positions (i.e., number of positions times number of feature maps), and there are
filters at layer
of shape. Then computing a feature map (applying an filter at all
pixel positions where the filter can be applied) costs
. The total cost is times that.
For a standard MLP, the cost would only be 
where there are different neurons at level.
所以CNN中每层 filter（一个 filter 产生一个feature map） 的数量应该比MLP中隐层神经元的个数少很多才行。
feature map 的大小在逐层减小（由于池化），所以低层网络 filter 的数量应该少一些，高层网络应该多一些。实际上，为了保证各层计算量差不多，the number of features map 和 the number of pixel positions 的乘积应该基本保持不变。这个乘积其实就是这层神经元的数量，也就是说每层神经元数量基本不变 to preserve the information about the input。
The number of feature maps directly controlscapacity and so that depends on the number of available examples and the complexity of the task.
Filter Shape
filter shapes的选择和数据集关系较大。
MNIST数据为28*28，第一层用5*5 filter 比较好；而对于其他自然图像（一般几百*几百像素），filter 12x12 or 15x15 比较合适。
The trick is thus to find the right level of “granularity” (i.e. filter shapes) in order tocreate abstractions at the proper scale, given a particular dataset.
Max Pooling Shape
通常是2x2 or no max-pooling。很大的图像可以用4x4 pooling。但要注意，这相当于维度减少了16倍，有可能损失了过多的信息。
Tips
可以通过以下两种技巧使结果更好：
1.对数据进行白化处理（PCA白化）
2.随着迭代次数衰减学习率