凸包之三道模板应用题

虽然有了现成的凸包算法，但是还有一些求得凸点前期或后期类问题需要自己解决。在这里来个小小的总结。
先贴出求凸包的算法:

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N=5e4+10;
struct point{
    int x,y;
}p[N];
int dis(point a,point b){
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
int cross(point p0,point p1,point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
int cmp1(point p1,point p2){
    return p1.x<p2.x||(p1.x==p2.x&&p1.y<p2.y);
}
int cmp2(point p1,point p2){
    int c=cross(p[0],p1,p2);
    if(c==0) return dis(p[0],p1)<dis(p[0],p2);
    return c>0;
}
point sta[N];
int top;
void convex(int n){
    top=0;
    sort(p,p+n,cmp1);
    sort(p+1,p+n,cmp2);
    sta[top++]=p[0];
    sta[top++]=p[1];
    for(int i=2;i<n;i++){
        if(cross(sta[top-2],sta[top-1],p[i])>0) sta[top++]=p[i];
        else {
            top--;
            while(top>=2&&cross(sta[top-2],sta[top-1],p[i])<=0) top--;
            sta[top++]=p[i];
        }
    }
}

int rotating()  //旋转卡壳
{
    int q=1,ans=0;
    sta[top]=sta[0];
    for(int i=0;i<top;i++)
    {
        while(cross(sta[i],sta[i+1],sta[q+1])>cross(sta[i],sta[i+1],sta[q]))
            q=(q+1)%top;
        ans=max(ans,max(dis(sta[i],sta[q]),dis(sta[i+1],sta[q+1])));
    }
    return ans;
}

SPOJ MTRIAREA - Maximum Triangle Area

http://www.spoj.com/problems/MTRIAREA/en/
题目：Given n distinct points on a plane, your task is to find the triangle that have the maximum area, whose vertices are from the given points.
分析：用凸包算法求得所有的凸点后直接寻找可以构成最大三角形的三个点。所以重点在于怎么找那三个点。
求最远点对算法带来灵感，由两个固定的点可以求出第三个离这条边最远的点，那么我们求出第三个点后再更新第二个点，最后更新第一个点。恩，就这样找那三个点。（较高效的三重循环）

寻找最大的面积：

double area(){
    double res=0;
    for(int i=0;i<top;i++){
        int j=(i+1)%top;
        int k=(j+1)%top;
        while(i!=j && k!=j){
        　　　while(k!=i && cross(ans[i],ans[j],ans[k+1])>cross(ans[i],ans[j],ans[k])) k=(k+1)%top;
             double temp=fabs(cross(ans[i],ans[j],ans[k]))/2;
             res=max(res,temp);
             j=(j+1)%top;
        }
    }
    return res;
}

hdu 5251 矩形面积

http://acm.hdu.edu.cn/showproblem.php?pid=5251
大意：给出n个矩形，求最小的矩形盖住所有的矩形其面积。

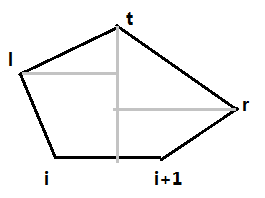
分析：先求出凸包，然后寻找相应的最小（最大）矩形。核心代码需结合上图理解：
已知相邻两点由旋转卡壳求出最远点，令len表示相邻点的距离，ｔ和ｉ、ｉ＋１的叉积除以len就是高度。设p离那个高最远，那么即是点积最大，同样用类似于求最远点的方法求得宽度。不过这次使用点积而不是叉积。就这样不断更新最大值——高×宽。

double work()
{
    int t,r,l;
    double res=999999999;
    t=r=1;
    if(top<3)
        return 0;
    for(int i=0; i<top; i++)
    {
        while(xmul(ans[i],ans[i+1],ans[t+1])>eps+xmul(ans[i],ans[i+1],ans[t]))
            t=(t+1)%top;
        while(dmul(ans[i],ans[i+1],ans[r+1])>eps+dmul(ans[i],ans[i+1],ans[r]))
            r=(r+1)%top;
        if(!i) l=r;
        while(dmul(ans[i],ans[i+1],ans[l+1])<=eps+dmul(ans[i],ans[i+1],ans[l]))
            l=(l+1)%top;
        double d=dis(ans[i],ans[i+1]);
        double tmp=xmul(ans[i],ans[i+1],ans[t])*
                   ( dmul(ans[i],ans[i+1],ans[r])-
                     dmul(ans[i],ans[i+1],ans[l]) )/d;
        res=min(res,tmp);
    }
    return res;
}

UVA 10652 Board Wrapping

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&category=533&problem=1593&mosmsg=Submission+received+with+ID+17384911
大意：给出ｎ个矩形的中心坐标、宽、高和旋转角度（宽轴和ｘ轴的夹角），求解所有的矩形的面积的和与最小包含他们的多边形的面积比，以百分数表示。
分析：由x,y,w,h,angle可以推算出所有的顶点坐标。即由坐标旋转的知识
（相关博文：http://blog.csdn.net/thearcticocean/article/details/50644718）
推得所有的四个顶点。

Vector Rotate(Vector A, double rad) {  
    return Vector(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}

p[pc++] = o + Rotate(Vector(-w/2, -h/2), ang);
p[pc++] = o + Rotate(Vector(w/2, -h/2), ang);
p[pc++] = o + Rotate(Vector(-w/2, h/2), ang);
p[pc++] = o + Rotate(Vector(w/2, h/2), ang);

计算多边形面积，使用叉积来个顶点循环即可（相关博文：http://blog.csdn.net/thearcticocean/article/details/47272197）

double area(point* p, int n) {
    double area = 0;
    for(int i = 1; i < n-1; i++) {
        area += cross(p[i]-p[0], p[i+1]-p[0]);
    }
    return area / 2;
}

恩，剩下的就是套模板了。

other

假设已知两条直线相交，且已知必须的四个点。那么我们可以通过如下方法求得交点：

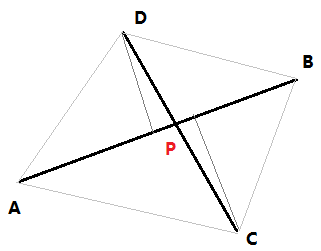
假设两线段是AB和CD，交点是P。（下面有许多变量替换）

xp−xDxp−xC=SABDSABC=xmul(A,B,D)xmul(A,B,C)=mdmc(xp−xD)mc=(xp−xC)mdxp=xD×mc−xC×mdmc−md

同理，可以求解p的y坐标。
yp=yD×mc−yC×mdmc−md

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

const double eps=1e-7;
struct point {
    double x,y;
    point(){};
    point(double _x,double _y) { x=_x;  y=_y; }
    void show(){
        printf("%.2lf %.2lf\n",x,y);
    }
};
double xmul(point p0,point p1,point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
point intersec(point A,point B,point C,point D){
    double md=xmul(A,B,D), mc=xmul(A,B,C);
    double x=(D.x*mc-C.x*md)/(mc-md);
    double y=(D.y*mc-C.y*md)/(mc-md);
    return point(x,y);
}
int main()
{
    freopen("cin1.txt","r",stdin);
    int n;
    cin>>n;
    while(n--){
        point A,B,C,D;
        scanf("%lf%lf%lf%lf",&A.x,&A.y,&B.x,&B.y);
        scanf("%lf%lf%lf%lf",&C.x,&C.y,&D.x,&D.y);
        intersec(A,B,C,D).show();
    }
    return 0;
}