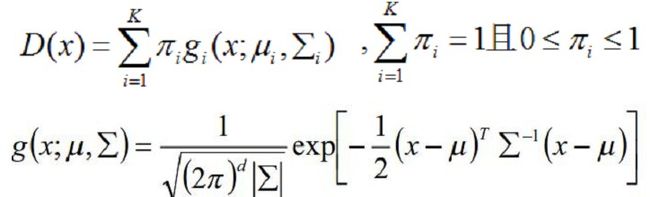Gruph-cut
所谓图像分割指的是根据灰度、颜色、纹理和形状等特征把图像划分成若干互不交迭的区域，并使这些特征在同一区域内呈现出相似性，而在不同区域间呈现出明显的差异性。我们先对目前主要的图像分割方法做个概述，后面再对个别方法做详细的了解和学习。
1、基于阈值的分割方法
阈值法的基本思想是基于图像的灰度特征来计算一个或多个灰度阈值，并将图像中每个像素的灰度值与阈值相比较，最后将像素根据比较结果分到合适的类别中。因此，该类方法最为关键的一步就是按照某个准则函数来求解最佳灰度阈值。
2、基于边缘的分割方法
所谓边缘是指图像中两个不同区域的边界线上连续的像素点的集合，是图像局部特征不连续性的反映，体现了灰度、颜色、纹理等图像特性的突变。通常情况下，基于边缘的分割方法指的是基于灰度值的边缘检测，它是建立在边缘灰度值会呈现出阶跃型或屋顶型变化这一观测基础上的方法。
阶跃型边缘两边像素点的灰度值存在着明显的差异，而屋顶型边缘则位于灰度值上升或下降的转折处。正是基于这一特性，可以使用微分算子进行边缘检测，即使用一阶导数的极值与二阶导数的过零点来确定边缘，具体实现时可以使用图像与模板进行卷积来完成。
3、基于区域的分割方法
此类方法是将图像按照相似性准则分成不同的区域，主要包括种子区域生长法、区域分裂合并法和分水岭法等几种类型。
种子区域生长法是从一组代表不同生长区域的种子像素开始，接下来将种子像素邻域里符合条件的像素合并到种子像素所代表的生长区域中，并将新添加的像素作为新的种子像素继续合并过程，直到找不到符合条件的新像素为止。该方法的关键是选择合适的初始种子像素以及合理的生长准则。
区域分裂合并法（Gonzalez，2002）的基本思想是首先将图像任意分成若干互不相交的区域，然后再按照相关准则对这些区域进行分裂或者合并从而完成分割任务，该方法既适用于灰度图像分割也适用于纹理图像分割。
分水岭法（Meyer，1990）是一种基于拓扑理论的数学形态学的分割方法，其基本思想是把图像看作是测地学上的拓扑地貌，图像中每一点像素的灰度值表示该点的海拔高度，每一个局部极小值及其影响区域称为集水盆，而集水盆的边界则形成分水岭。该算法的实现可以模拟成洪水淹没的过程，图像的最低点首先被淹没，然后水逐渐淹没整个山谷。当水位到达一定高度的时候将会溢出，这时在水溢出的地方修建堤坝，重复这个过程直到整个图像上的点全部被淹没，这时所建立的一系列堤坝就成为分开各个盆地的分水岭。分水岭算法对微弱的边缘有着良好的响应，但图像中的噪声会使分水岭算法产生过分割的现象。
4、基于图论的分割方法
此类方法把图像分割问题与图的最小割（min cut）问题相关联。首先将图像映射为带权无向图G=<V，E>，图中每个节点N∈V对应于图像中的每个像素，每条边∈E连接着一对相邻的像素，边的权值表示了相邻像素之间在灰度、颜色或纹理方面的非负相似度。而对图像的一个分割s就是对图的一个剪切，被分割的每个区域C∈S对应着图中的一个子图。而分割的最优原则就是使划分后的子图在内部保持相似度最大，而子图之间的相似度保持最小。基于图论的分割方法的本质就是移除特定的边，将图划分为若干子图从而实现分割。目前所了解到的基于图论的方法有GraphCut，GrabCut和Random Walk等。
5、基于能量泛函的分割方法
该类方法主要指的是活动轮廓模型（active contour model）以及在其基础上发展出来的算法，其基本思想是使用连续曲线来表达目标边缘，并定义一个能量泛函使得其自变量包括边缘曲线，因此分割过程就转变为求解能量泛函的最小值的过程，一般可通过求解函数对应的欧拉(Euler．Lagrange)方程来实现，能量达到最小时的曲线位置就是目标的轮廓所在。按照模型中曲线表达形式的不同，活动轮廓模型可以分为两大类：参数活动轮廓模型（parametric active contour model）和几何活动轮廓模型（geometric active contour model）。
参数活动轮廓模型是基于Lagrange框架，直接以曲线的参数化形式来表达曲线，最具代表性的是由Kasset a1(1987)所提出的Snake模型。该类模型在早期的生物图像分割领域得到了成功的应用，但其存在着分割结果受初始轮廓的设置影响较大以及难以处理曲线拓扑结构变化等缺点，此外其能量泛函只依赖于曲线参数的选择，与物体的几何形状无关，这也限制了其进一步的应用。
几何活动轮廓模型的曲线运动过程是基于曲线的几何度量参数而非曲线的表达参数，因此可以较好地处理拓扑结构的变化，并可以解决参数活动轮廓模型难以解决的问题。而水平集（Level Set）方法（Osher，1988）的引入，则极大地推动了几何活动轮廓模型的发展，因此几何活动轮廓模型一般也可被称为水平集方法。
———————————————————————————————————————————————————
上一文对主要的分割方法做了一个概述。那下面我们对其中几个比较感兴趣的算法做个学习。下面主要是Graph Cut，下一个博文我们再学习下Grab Cut，两者都是基于图论的分割方法。另外OpenCV实现了Grab Cut，具体的源码解读见博文更新。接触时间有限，若有错误，还望各位前辈指正，谢谢。
Graph cuts是一种十分有用和流行的能量优化算法，在计算机视觉领域普遍应用于前背景分割（Image segmentation）、立体视觉（stereo vision）、抠图（Image matting）等。
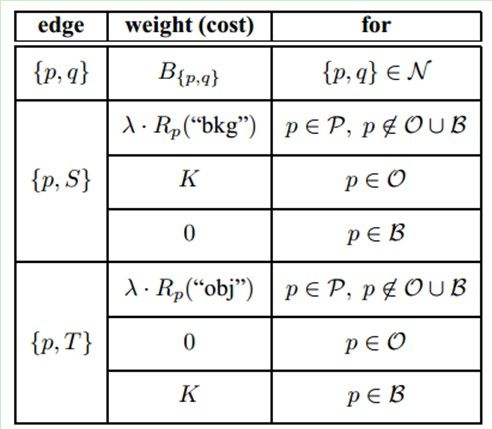
此类方法把图像分割问题与图的最小割（min cut）问题相关联。首先用一个无向图G=<V，E>表示要分割的图像，V和E分别是顶点（vertex）和边（edge）的集合。此处的Graph和普通的Graph稍有不同。普通的图由顶点和边构成，如果边的有方向的，这样的图被则称为有向图，否则为无向图，且边是有权值的，不同的边可以有不同的权值，分别代表不同的物理意义。而Graph Cuts图是在普通图的基础上多了2个顶点，这2个顶点分别用符号”S”和”T”表示，统称为终端顶点。其它所有的顶点都必须和这2个顶点相连形成边集合中的一部分。所以Graph Cuts中有两种顶点，也有两种边。
第一种顶点和边是：第一种普通顶点对应于图像中的每个像素。每两个邻域顶点（对应于图像中每两个邻域像素）的连接就是一条边。这种边也叫n-links。
第二种顶点和边是：除图像像素外，还有另外两个终端顶点，叫S（source：源点，取源头之意）和T（sink：汇点，取汇聚之意）。每个普通顶点和这2个终端顶点之间都有连接，组成第二种边。这种边也叫t-links。
上图就是一个图像对应的s-t图，每个像素对应图中的一个相应顶点，另外还有s和t两个顶点。上图有两种边，实线的边表示每两个邻域普通顶点连接的边n-links，虚线的边表示每个普通顶点与s和t连接的边t-links。在前后景分割中，s一般表示前景目标，t一般表示背景。
图中每条边都有一个非负的权值we，也可以理解为cost（代价或者费用）。一个cut（割）就是图中边集合E的一个子集C，那这个割的cost（表示为|C|）就是边子集C的所有边的权值的总和。
Graph Cuts中的Cuts是指这样一个边的集合，很显然这些边集合包括了上面2种边，该集合中所有边的断开会导致残留”S”和”T”图的分开，所以就称为“割”。如果一个割，它的边的所有权值之和最小，那么这个就称为最小割，也就是图割的结果。而福特-富克森定理表明，网路的最大流max flow与最小割min cut相等。所以由Boykov和Kolmogorov发明的max-flow/min-cut算法就可以用来获得s-t图的最小割。这个最小割把图的顶点划分为两个不相交的子集S和T，其中s ∈S，t∈ T和S∪T=V 。这两个子集就对应于图像的前景像素集和背景像素集，那就相当于完成了图像分割。
也就是说图中边的权值就决定了最后的分割结果，那么这些边的权值怎么确定呢？
图像分割可以看成pixel labeling（像素标记）问题，目标（s-node）的label设为1，背景（t-node）的label设为0，这个过程可以通过最小化图割来最小化能量函数得到。那很明显，发生在目标和背景的边界处的cut就是我们想要的（相当于把图像中背景和目标连接的地方割开，那就相当于把其分割了）。同时，这时候能量也应该是最小的。假设整幅图像的标签label（每个像素的label）为L= {l1,l2,,,, lp }，其中li为0（背景）或者1（目标）。那假设图像的分割为L时，图像的能量可以表示为：
E(L)=aR(L)+B(L)
其中，R(L)为区域项（regional term），B(L)为边界项（boundary term），而a就是区域项和边界项之间的重要因子，决定它们对能量的影响大小。如果a为0，那么就只考虑边界因素，不考虑区域因素。E(L)表示的是权值，即损失函数，也叫能量函数，图割的目标就是优化能量函数使其值达到最小。
区域项：
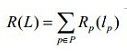，其中Rp(lp)表示为像素p分配标签lp的惩罚，Rp(lp)能量项的权值可以通过比较像素p的灰度和给定的目标和前景的灰度直方图来获得，换句话说就是像素p属于标签lp的概率，我希望像素p分配为其概率最大的标签lp，这时候我们希望能量最小，所以一般取概率的负对数值，故t-link的权值如下：
Rp(1) = -ln Pr(Ip|’obj’)； Rp(0) = -ln Pr(Ip|’bkg’)
由上面两个公式可以看到，当像素p的灰度值属于目标的概率Pr(Ip|’obj’)大于背景Pr(Ip|’bkg’)，那么Rp(1)就小于Rp(0)，也就是说当像素p更有可能属于目标时，将p归类为目标就会使能量R(L)小。那么，如果全部的像素都被正确划分为目标或者背景，那么这时候能量就是最小的。
边界项：
其中，p和q为邻域像素，边界平滑项主要体现分割L的边界属性，B<p,q>可以解析为像素p和q之间不连续的惩罚，一般来说如果p和q越相似（例如它们的灰度），那么B<p,q>越大，如果他们非常不同，那么B<p,q>就接近于0。换句话说，如果两邻域像素差别很小，那么它属于同一个目标或者同一背景的可能性就很大，如果他们的差别很大，那说明这两个像素很有可能处于目标和背景的边缘部分，则被分割开的可能性比较大，所以当两邻域像素差别越大，B<p,q>越小，即能量越小。
好了，现在我们来总结一下：我们目标是将一幅图像分为目标和背景两个不相交的部分，我们运用图分割技术来实现。首先，图由顶点和边来组成，边有权值。那我们需要构建一个图，这个图有两类顶点，两类边和两类权值。普通顶点由图像每个像素组成，然后每两个邻域像素之间存在一条边，它的权值由上面说的“边界平滑能量项”来决定。还有两个终端顶点s（目标）和t（背景），每个普通顶点和s都存在连接，也就是边，边的权值由“区域能量项”Rp(1)来决定，每个普通顶点和t连接的边的权值由“区域能量项”Rp(0)来决定。这样所有边的权值就可以确定了，也就是图就确定了。这时候，就可以通过min cut算法来找到最小的割，这个min cut就是权值和最小的边的集合，这些边的断开恰好可以使目标和背景被分割开，也就是min cut对应于能量的最小化。而min cut和图的max flow是等效的，故可以通过max flow算法来找到s-t图的min cut。目前的算法主要有：
1) Goldberg-Tarjan
2) Ford-Fulkerson
3) 上诉两种方法的改进算法
权值：
Graph cut的3x3图像分割示意图：我们取两个种子点（就是人为的指定分别属于目标和背景的两个像素点），然后我们建立一个图，图中边的粗细表示对应权值的大小，然后找到权值和最小的边的组合，也就是（c）中的cut，即完成了图像分割的功能。
上面具体的细节请参考：
《Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images》（Boykov，iccv01）这篇paper讲怎么用graphcut来做image segmentation。
在Boykov 和 Kolmogorov 俩人的主页上就有大量的code。包括maxflow/min-cut、stereo algorithms等算法：
http://pub.ist.ac.at/~vnk/software.html
http://vision.csd.uwo.ca/code/
康奈尔大学的graphcuts研究主页也有不少信息：
http://www.cs.cornell.edu/~rdz/graphcuts.html
《Image Segmentation: A Survey of Graph-cut Methods》（Faliu Yi，ICSAI 2012）
———————————————————————————————————————————————————
上一文对GraphCut做了一个了解，而现在我们聊到的GrabCut是对其的改进版，是迭代的Graph Cut。OpenCV中的GrabCut算法是依据《"GrabCut" - Interactive Foreground Extraction using Iterated Graph Cuts》这篇文章来实现的。该算法利用了图像中的纹理（颜色）信息和边界（反差）信息，只要少量的用户交互操作即可得到比较好的分割结果。那下面我们来了解这个论文的一些细节。另外OpenCV实现的GrabCut的源码解读见下一个博文。接触时间有限，若有错误，还望各位前辈指正，谢谢。
GrabCut是微软研究院的一个课题，主要功能是分割和抠图。个人理解它的卖点在于：
（1）你只需要在目标外面画一个框，把目标框住，它就可以完成良好的分割：
（2）如果增加额外的用户交互（由用户指定一些像素属于目标），那么效果就可以更完美：
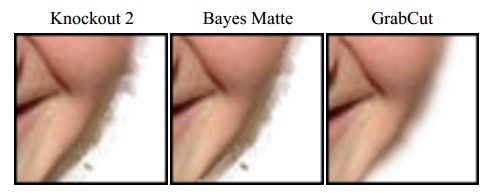
（3）它的Border Matting技术会使目标分割边界更加自然和perfect：
当然了，它也有不完美的地方，一是没有任何一个算法可以放之四海而皆准，它也不例外，如果背景比较复杂或者背景和目标相似度很大，那分割就不太好了；二是速度有点慢。当然了，现在也有不少关于提速的改进。
OK，那看了效果，我们会想，上面这些效果是怎么达到的呢？它和Graph Cut有何不同？
（1）Graph Cut的目标和背景的模型是灰度直方图，Grab Cut取代为RGB三通道的混合高斯模型GMM；
（2）Graph Cut的能量最小化（分割）是一次达到的，而Grab Cut取代为一个不断进行分割估计和模型参数学习的交互迭代过程；
（3）Graph Cut需要用户指定目标和背景的一些种子点，但是Grab Cut只需要提供背景区域的像素集就可以了。也就是说你只需要框选目标，那么在方框外的像素全部当成背景，这时候就可以对GMM进行建模和完成良好的分割了。即Grab Cut允许不完全的标注（incomplete labelling）。
1、颜色模型
我们采用RGB颜色空间，分别用一个K个高斯分量（一取般K=5）的全协方差GMM（混合高斯模型）来对目标和背景进行建模。于是就存在一个额外的向量k = {k1, . . ., kn, . . ., kN}，其中kn就是第n个像素对应于哪个高斯分量，kn∈ {1, . . . K}。对于每个像素，要不来自于目标GMM的某个高斯分量，要不就来自于背景GMM的某个高斯分量。
所以用于整个图像的Gibbs能量为（式7）：
其中，U就是区域项，和上一文说的一样，你表示一个像素被归类为目标或者背景的惩罚，也就是某个像素属于目标或者背景的概率的负对数。我们知道混合高斯密度模型是如下形式：
所以取负对数之后就变成式（9）那样的形式了，其中GMM的参数θ就有三个：每一个高斯分量的权重π、每个高斯分量的均值向量u（因为有RGB三个通道，故为三个元素向量）和协方差矩阵∑（因为有RGB三个通道，故为3x3矩阵）。如式（10）。也就是说描述目标的GMM和描述背景的GMM的这三个参数都需要学习确定。一旦确定了这三个参数，那么我们知道一个像素的RGB颜色值之后，就可以代入目标的GMM和背景的GMM，就可以得到该像素分别属于目标和背景的概率了，也就是Gibbs能量的区域能量项就可以确定了，即图的t-link的权值我们就可以求出。那么n-link的权值怎么求呢？也就是边界能量项V怎么求？
边界项和之前说的Graph Cut的差不多，体现邻域像素m和n之间不连续的惩罚，如果两邻域像素差别很小，那么它属于同一个目标或者同一背景的可能性就很大，如果他们的差别很大，那说明这两个像素很有可能处于目标和背景的边缘部分，则被分割开的可能性比较大，所以当两邻域像素差别越大，能量越小。而在RGB空间中，衡量两像素的相似性，我们采用欧式距离（二范数）。这里面的参数β由图像的对比度决定，可以想象，如果图像的对比度较低，也就是说本身有差别的像素m和n，它们的差||zm-zn||还是比较低，那么我们需要乘以一个比较大的β来放大这种差别，而对于对比度高的图像，那么也许本身属于同一目标的像素m和n的差||zm-zn||还是比较高，那么我们就需要乘以一个比较小的β来缩小这种差别，使得V项能在对比度高或者低的情况下都可以正常工作。常数γ为50（经过作者用15张图像训练得到的比较好的值）。OK，那这时候，n-link的权值就可以通过式（11）来确定了，这时候我们想要的图就可以得到了，我们就可以对其进行分割了。
2、迭代能量最小化分割算法
Graph Cut的算法是一次性最小化的，而Grab Cut是迭代最小的，每次迭代过程都使得对目标和背景建模的GMM的参数更优，使得图像分割更优。我们直接通过算法来说明：
2.1、初始化
（1）用户通过直接框选目标来得到一个初始的trimap T，即方框外的像素全部作为背景像素TB，而方框内TU的像素全部作为“可能是目标”的像素。
（2）对TB内的每一像素n，初始化像素n的标签αn=0，即为背景像素；而对TU内的每个像素n，初始化像素n的标签αn=1，即作为“可能是目标”的像素。
（3）经过上面两个步骤，我们就可以分别得到属于目标（αn=1）的一些像素，剩下的为属于背景（αn=0）的像素，这时候，我们就可以通过这个像素来估计目标和背景的GMM了。我们可以通过k-mean算法分别把属于目标和背景的像素聚类为K类，即GMM中的K个高斯模型，这时候GMM中每个高斯模型就具有了一些像素样本集，这时候它的参数均值和协方差就可以通过他们的RGB值估计得到，而该高斯分量的权值可以通过属于该高斯分量的像素个数与总的像素个数的比值来确定。
2.2、迭代最小化
（1）对每个像素分配GMM中的高斯分量（例如像素n是目标像素，那么把像素n的RGB值代入目标GMM中的每一个高斯分量中，概率最大的那个就是最有可能生成n的，也即像素n的第kn个高斯分量）：
（2）对于给定的图像数据Z，学习优化GMM的参数（因为在步骤（1）中我们已经为每个像素归为哪个高斯分量做了归类，那么每个高斯模型就具有了一些像素样本集，这时候它的参数均值和协方差就可以通过这些像素样本的RGB值估计得到，而该高斯分量的权值可以通过属于该高斯分量的像素个数与总的像素个数的比值来确定。）：
（3）分割估计（通过1中分析的Gibbs能量项，建立一个图，并求出权值t-link和n-link，然后通过max flow/min cut算法来进行分割）：
（4）重复步骤（1）到（3），直到收敛。经过（3）的分割后，每个像素属于目标GMM还是背景GMM就变了，所以每个像素的kn就变了，故GMM也变了，所以每次的迭代会交互地优化GMM模型和分割结果。另外，因为步骤（1）到（3）的过程都是能量递减的过程，所以可以保证迭代过程会收敛。
（5）采用border matting对分割的边界进行平滑等等后期处理。
2.3、用户编辑（交互）
（1）编辑：人为地固定一些像素是目标或者背景像素，然后再执行一次2.2中步骤（3）；
（2）重操作：重复整个迭代算法。（可选，实际上这里是程序或者软件抠图的撤销作用）
总的来说，其中关键在于目标和背景的概率密度函数模型和图像分割可以交替迭代优化的过程。更多的细节请参考原文。
《“GrabCut” — Interactive Foreground Extraction using Iterated Graph Cuts》
http://research.microsoft.com/en-us/um/people/ablake/papers/ablake/siggraph04.pdf
OpenCV实现了这个算法（没有后面的border matting过程），下一文我们再解读下它的源代码。
———————————————————————————————————————————————————
上一文对GrabCut做了一个了解。OpenCV中的GrabCut算法是依据《"GrabCut" - Interactive Foreground Extraction using Iterated Graph Cuts》这篇文章来实现的。现在我对源码做了些注释，以便我们更深入的了解该算法。一直觉得论文和代码是有比较大的差别的，个人觉得脱离代码看论文，最多能看懂70%，剩下20%或者更多就需要通过阅读代码来获得了，那还有10%就和每个人的基础和知识储备相挂钩了。
接触时间有限，若有错误，还望各位前辈指正，谢谢。原论文的一些浅解见上一博文：
http://blog.csdn.net/zouxy09/article/details/8534954
一、GrabCut函数使用
在OpenCV的源码目录的samples的文件夹下，有grabCut的使用例程，请参考：
opencv\samples\cpp\grabcut.cpp。
而grabCut函数的API说明如下：
void cv::grabCut( InputArray _img, InputOutputArray _mask, Rect rect,
InputOutputArray _bgdModel, InputOutputArray _fgdModel,
int iterCount, int mode )
/*
****参数说明：
img——待分割的源图像，必须是8位3通道（CV_8UC3）图像，在处理的过程中不会被修改；
mask——掩码图像，如果使用掩码进行初始化，那么mask保存初始化掩码信息；在执行分割的时候，也可以将用户交互所设定的前景与背景保存到mask中，然后再传入grabCut函数；在处理结束之后，mask中会保存结果。mask只能取以下四种值：
GCD_BGD（=0），背景；
GCD_FGD（=1），前景；
GCD_PR_BGD（=2），可能的背景；
GCD_PR_FGD（=3），可能的前景。
如果没有手工标记GCD_BGD或者GCD_FGD，那么结果只会有GCD_PR_BGD或GCD_PR_FGD；
rect——用于限定需要进行分割的图像范围，只有该矩形窗口内的图像部分才被处理；
bgdModel——背景模型，如果为null，函数内部会自动创建一个bgdModel；bgdModel必须是单通道浮点型（CV_32FC1）图像，且行数只能为1，列数只能为13x5；
fgdModel——前景模型，如果为null，函数内部会自动创建一个fgdModel；fgdModel必须是单通道浮点型（CV_32FC1）图像，且行数只能为1，列数只能为13x5；
iterCount——迭代次数，必须大于0；
mode——用于指示grabCut函数进行什么操作，可选的值有：
GC_INIT_WITH_RECT（=0），用矩形窗初始化GrabCut；
GC_INIT_WITH_MASK（=1），用掩码图像初始化GrabCut；
GC_EVAL（=2），执行分割。
*/
二、GrabCut源码解读
其中源码包含了gcgraph.hpp这个构建图和max flow/min cut算法的实现文件，这个文件暂时没有解读，后面再更新了。
/*M///////////////////////////////////////////////////////////////////////////////////////
//
// IMPORTANT: READ BEFORE DOWNLOADING, COPYING, INSTALLING OR USING.
//
// By downloading, copying, installing or using the software you agree to this license.
// If you do not agree to this license, do not download, install,
// copy or use the software.
//
//
// Intel License Agreement
// For Open Source Computer Vision Library
//
// Copyright (C) 2000, Intel Corporation, all rights reserved.
// Third party copyrights are property of their respective owners.
//
// Redistribution and use in source and binary forms, with or without modification,
// are permitted provided that the following conditions are met:
//
// * Redistribution's of source code must retain the above copyright notice,
// this list of conditions and the following disclaimer.
//
// * Redistribution's in binary form must reproduce the above copyright notice,
// this list of conditions and the following disclaimer in the documentation
// and/or other materials provided with the distribution.
//
// * The name of Intel Corporation may not be used to endorse or promote products
// derived from this software without specific prior written permission.
//
// This software is provided by the copyright holders and contributors "as is" and
// any express or implied warranties, including, but not limited to, the implied
// warranties of merchantability and fitness for a particular purpose are disclaimed.
// In no event shall the Intel Corporation or contributors be liable for any direct,
// indirect, incidental, special, exemplary, or consequential damages
// (including, but not limited to, procurement of substitute goods or services;
// loss of use, data, or profits; or business interruption) however caused
// and on any theory of liability, whether in contract, strict liability,
// or tort (including negligence or otherwise) arising in any way out of
// the use of this software, even if advised of the possibility of such damage.
//
//M*/
#include "precomp.hpp"
#include "gcgraph.hpp"
#include <limits>
using namespace cv;
/*
This is implementation of image segmentation algorithm GrabCut described in
"GrabCut — Interactive Foreground Extraction using Iterated Graph Cuts".
Carsten Rother, Vladimir Kolmogorov, Andrew Blake.
*/
/*
GMM - Gaussian Mixture Model
*/
class GMM
{
public:
static const int componentsCount = 5;
GMM( Mat& _model );
double operator()( const Vec3d color ) const;
double operator()( int ci, const Vec3d color ) const;
int whichComponent( const Vec3d color ) const;
void initLearning();
void addSample( int ci, const Vec3d color );
void endLearning();
private:
void calcInverseCovAndDeterm( int ci );
Mat model;
double* coefs;
double* mean;
double* cov;
double inverseCovs[componentsCount][3][3]; //协方差的逆矩阵
double covDeterms[componentsCount]; //协方差的行列式
double sums[componentsCount][3];
double prods[componentsCount][3][3];
int sampleCounts[componentsCount];
int totalSampleCount;
};
//背景和前景各有一个对应的GMM（混合高斯模型）
GMM::GMM( Mat& _model )
{
//一个像素的（唯一对应）高斯模型的参数个数或者说一个高斯模型的参数个数
//一个像素RGB三个通道值，故3个均值，3*3个协方差，共用一个权值
const int modelSize = 3/*mean*/ + 9/*covariance*/ + 1/*component weight*/;
if( _model.empty() )
{
//一个GMM共有componentsCount个高斯模型，一个高斯模型有modelSize个模型参数
_model.create( 1, modelSize*componentsCount, CV_64FC1 );
_model.setTo(Scalar(0));
}
else if( (_model.type() != CV_64FC1) || (_model.rows != 1) || (_model.cols != modelSize*componentsCount) )
CV_Error( CV_StsBadArg, "_model must have CV_64FC1 type, rows == 1 and cols == 13*componentsCount" );
model = _model;
//注意这些模型参数的存储方式：先排完componentsCount个coefs，再3*componentsCount个mean。
//再3*3*componentsCount个cov。
coefs = model.ptr<double>(0); //GMM的每个像素的高斯模型的权值变量起始存储指针
mean = coefs + componentsCount; //均值变量起始存储指针
cov = mean + 3*componentsCount; //协方差变量起始存储指针
for( int ci = 0; ci < componentsCount; ci++ )
if( coefs[ci] > 0 )
//计算GMM中第ci个高斯模型的协方差的逆Inverse和行列式Determinant
//为了后面计算每个像素属于该高斯模型的概率（也就是数据能量项）
calcInverseCovAndDeterm( ci );
}
//计算一个像素（由color=（B,G,R）三维double型向量来表示）属于这个GMM混合高斯模型的概率。
//也就是把这个像素像素属于componentsCount个高斯模型的概率与对应的权值相乘再相加，
//具体见论文的公式（10）。结果从res返回。
//这个相当于计算Gibbs能量的第一个能量项（取负后）。
double GMM::operator()( const Vec3d color ) const
{
double res = 0;
for( int ci = 0; ci < componentsCount; ci++ )
res += coefs[ci] * (*this)(ci, color );
return res;
}
//计算一个像素（由color=（B,G,R）三维double型向量来表示）属于第ci个高斯模型的概率。
//具体过程，即高阶的高斯密度模型计算式，具体见论文的公式（10）。结果从res返回
double GMM::operator()( int ci, const Vec3d color ) const
{
double res = 0;
if( coefs[ci] > 0 )
{
CV_Assert( covDeterms[ci] > std::numeric_limits<double>::epsilon() );
Vec3d diff = color;
double* m = mean + 3*ci;
diff[0] -= m[0]; diff[1] -= m[1]; diff[2] -= m[2];
double mult = diff[0]*(diff[0]*inverseCovs[ci][0][0] + diff[1]*inverseCovs[ci][1][0] + diff[2]*inverseCovs[ci][2][0])
+ diff[1]*(diff[0]*inverseCovs[ci][0][1] + diff[1]*inverseCovs[ci][1][1] + diff[2]*inverseCovs[ci][2][1])
+ diff[2]*(diff[0]*inverseCovs[ci][0][2] + diff[1]*inverseCovs[ci][1][2] + diff[2]*inverseCovs[ci][2][2]);
res = 1.0f/sqrt(covDeterms[ci]) * exp(-0.5f*mult);
}
return res;
}
//返回这个像素最有可能属于GMM中的哪个高斯模型（概率最大的那个）
int GMM::whichComponent( const Vec3d color ) const
{
int k = 0;
double max = 0;
for( int ci = 0; ci < componentsCount; ci++ )
{
double p = (*this)( ci, color );
if( p > max )
{
k = ci; //找到概率最大的那个，或者说计算结果最大的那个
max = p;
}
}
return k;
}
//GMM参数学习前的初始化，主要是对要求和的变量置零
void GMM::initLearning()
{
for( int ci = 0; ci < componentsCount; ci++)
{
sums[ci][0] = sums[ci][1] = sums[ci][2] = 0;
prods[ci][0][0] = prods[ci][0][1] = prods[ci][0][2] = 0;
prods[ci][1][0] = prods[ci][1][1] = prods[ci][1][2] = 0;
prods[ci][2][0] = prods[ci][2][1] = prods[ci][2][2] = 0;
sampleCounts[ci] = 0;
}
totalSampleCount = 0;
}
//增加样本，即为前景或者背景GMM的第ci个高斯模型的像素集（这个像素集是来用估
//计计算这个高斯模型的参数的）增加样本像素。计算加入color这个像素后，像素集
//中所有像素的RGB三个通道的和sums（用来计算均值），还有它的prods（用来计算协方差），
//并且记录这个像素集的像素个数和总的像素个数（用来计算这个高斯模型的权值）。
void GMM::addSample( int ci, const Vec3d color )
{
sums[ci][0] += color[0]; sums[ci][1] += color[1]; sums[ci][2] += color[2];
prods[ci][0][0] += color[0]*color[0]; prods[ci][0][1] += color[0]*color[1]; prods[ci][0][2] += color[0]*color[2];
prods[ci][1][0] += color[1]*color[0]; prods[ci][1][1] += color[1]*color[1]; prods[ci][1][2] += color[1]*color[2];
prods[ci][2][0] += color[2]*color[0]; prods[ci][2][1] += color[2]*color[1]; prods[ci][2][2] += color[2]*color[2];
sampleCounts[ci]++;
totalSampleCount++;
}
//从图像数据中学习GMM的参数：每一个高斯分量的权值、均值和协方差矩阵；
//这里相当于论文中“Iterative minimisation”的step 2
void GMM::endLearning()
{
const double variance = 0.01;
for( int ci = 0; ci < componentsCount; ci++ )
{
int n = sampleCounts[ci]; //第ci个高斯模型的样本像素个数
if( n == 0 )
coefs[ci] = 0;
else
{
//计算第ci个高斯模型的权值系数
coefs[ci] = (double)n/totalSampleCount;
//计算第ci个高斯模型的均值
double* m = mean + 3*ci;
m[0] = sums[ci][0]/n; m[1] = sums[ci][1]/n; m[2] = sums[ci][2]/n;
//计算第ci个高斯模型的协方差
double* c = cov + 9*ci;
c[0] = prods[ci][0][0]/n - m[0]*m[0]; c[1] = prods[ci][0][1]/n - m[0]*m[1]; c[2] = prods[ci][0][2]/n - m[0]*m[2];
c[3] = prods[ci][1][0]/n - m[1]*m[0]; c[4] = prods[ci][1][1]/n - m[1]*m[1]; c[5] = prods[ci][1][2]/n - m[1]*m[2];
c[6] = prods[ci][2][0]/n - m[2]*m[0]; c[7] = prods[ci][2][1]/n - m[2]*m[1]; c[8] = prods[ci][2][2]/n - m[2]*m[2];
//计算第ci个高斯模型的协方差的行列式
double dtrm = c[0]*(c[4]*c[8]-c[5]*c[7]) - c[1]*(c[3]*c[8]-c[5]*c[6]) + c[2]*(c[3]*c[7]-c[4]*c[6]);
if( dtrm <= std::numeric_limits<double>::epsilon() )
{
//相当于如果行列式小于等于0，（对角线元素）增加白噪声，避免其变
//为退化（降秩）协方差矩阵（不存在逆矩阵，但后面的计算需要计算逆矩阵）。
// Adds the white noise to avoid singular covariance matrix.
c[0] += variance;
c[4] += variance;
c[8] += variance;
}
//计算第ci个高斯模型的协方差的逆Inverse和行列式Determinant
calcInverseCovAndDeterm(ci);
}
}
}
//计算协方差的逆Inverse和行列式Determinant
void GMM::calcInverseCovAndDeterm( int ci )
{
if( coefs[ci] > 0 )
{
//取第ci个高斯模型的协方差的起始指针
double *c = cov + 9*ci;
double dtrm =
covDeterms[ci] = c[0]*(c[4]*c[8]-c[5]*c[7]) - c[1]*(c[3]*c[8]-c[5]*c[6])
+ c[2]*(c[3]*c[7]-c[4]*c[6]);
//在C++中，每一种内置的数据类型都拥有不同的属性, 使用<limits>库可以获
//得这些基本数据类型的数值属性。因为浮点算法的截断，所以使得，当a=2，
//b=3时 10*a/b == 20/b不成立。那怎么办呢？
//这个小正数（epsilon）常量就来了，小正数通常为可用给定数据类型的
//大于1的最小值与1之差来表示。若dtrm结果不大于小正数，那么它几乎为零。
//所以下式保证dtrm>0，即行列式的计算正确（协方差对称正定，故行列式大于0）。
CV_Assert( dtrm > std::numeric_limits<double>::epsilon() );
//三阶方阵的求逆
inverseCovs[ci][0][0] = (c[4]*c[8] - c[5]*c[7]) / dtrm;
inverseCovs[ci][1][0] = -(c[3]*c[8] - c[5]*c[6]) / dtrm;
inverseCovs[ci][2][0] = (c[3]*c[7] - c[4]*c[6]) / dtrm;
inverseCovs[ci][0][1] = -(c[1]*c[8] - c[2]*c[7]) / dtrm;
inverseCovs[ci][1][1] = (c[0]*c[8] - c[2]*c[6]) / dtrm;
inverseCovs[ci][2][1] = -(c[0]*c[7] - c[1]*c[6]) / dtrm;
inverseCovs[ci][0][2] = (c[1]*c[5] - c[2]*c[4]) / dtrm;
inverseCovs[ci][1][2] = -(c[0]*c[5] - c[2]*c[3]) / dtrm;
inverseCovs[ci][2][2] = (c[0]*c[4] - c[1]*c[3]) / dtrm;
}
}
//计算beta，也就是Gibbs能量项中的第二项（平滑项）中的指数项的beta，用来调整
//高或者低对比度时，两个邻域像素的差别的影响的，例如在低对比度时，两个邻域
//像素的差别可能就会比较小，这时候需要乘以一个较大的beta来放大这个差别，
//在高对比度时，则需要缩小本身就比较大的差别。
//所以我们需要分析整幅图像的对比度来确定参数beta，具体的见论文公式（5）。
/*
Calculate beta - parameter of GrabCut algorithm.
beta = 1/(2*avg(sqr(||color[i] - color[j]||)))
*/
static double calcBeta( const Mat& img )
{
double beta = 0;
for( int y = 0; y < img.rows; y++ )
{
for( int x = 0; x < img.cols; x++ )
{
//计算四个方向邻域两像素的差别，也就是欧式距离或者说二阶范数
//（当所有像素都算完后，就相当于计算八邻域的像素差了）
Vec3d color = img.at<Vec3b>(y,x);
if( x>0 ) // left >0的判断是为了避免在图像边界的时候还计算，导致越界
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y,x-1);
beta += diff.dot(diff); //矩阵的点乘，也就是各个元素平方的和
}
if( y>0 && x>0 ) // upleft
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y-1,x-1);
beta += diff.dot(diff);
}
if( y>0 ) // up
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y-1,x);
beta += diff.dot(diff);
}
if( y>0 && x<img.cols-1) // upright
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y-1,x+1);
beta += diff.dot(diff);
}
}
}
if( beta <= std::numeric_limits<double>::epsilon() )
beta = 0;
else
beta = 1.f / (2 * beta/(4*img.cols*img.rows - 3*img.cols - 3*img.rows + 2) ); //论文公式（5）
return beta;
}
//计算图每个非端点顶点（也就是每个像素作为图的一个顶点，不包括源点s和汇点t）与邻域顶点
//的边的权值。由于是无向图，我们计算的是八邻域，那么对于一个顶点，我们计算四个方向就行，
//在其他的顶点计算的时候，会把剩余那四个方向的权值计算出来。这样整个图算完后，每个顶点
//与八邻域的顶点的边的权值就都计算出来了。
//这个相当于计算Gibbs能量的第二个能量项（平滑项），具体见论文中公式（4）
/*
Calculate weights of noterminal vertices of graph.
beta and gamma - parameters of GrabCut algorithm.
*/
static void calcNWeights( const Mat& img, Mat& leftW, Mat& upleftW, Mat& upW,
Mat& uprightW, double beta, double gamma )
{
//gammaDivSqrt2相当于公式（4）中的gamma * dis(i,j)^(-1)，那么可以知道，
//当i和j是垂直或者水平关系时，dis(i,j)=1，当是对角关系时，dis(i,j)=sqrt(2.0f)。
//具体计算时，看下面就明白了
const double gammaDivSqrt2 = gamma / std::sqrt(2.0f);
//每个方向的边的权值通过一个和图大小相等的Mat来保存
leftW.create( img.rows, img.cols, CV_64FC1 );
upleftW.create( img.rows, img.cols, CV_64FC1 );
upW.create( img.rows, img.cols, CV_64FC1 );
uprightW.create( img.rows, img.cols, CV_64FC1 );
for( int y = 0; y < img.rows; y++ )
{
for( int x = 0; x < img.cols; x++ )
{
Vec3d color = img.at<Vec3b>(y,x);
if( x-1>=0 ) // left //避免图的边界
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y,x-1);
leftW.at<double>(y,x) = gamma * exp(-beta*diff.dot(diff));
}
else
leftW.at<double>(y,x) = 0;
if( x-1>=0 && y-1>=0 ) // upleft
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y-1,x-1);
upleftW.at<double>(y,x) = gammaDivSqrt2 * exp(-beta*diff.dot(diff));
}
else
upleftW.at<double>(y,x) = 0;
if( y-1>=0 ) // up
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y-1,x);
upW.at<double>(y,x) = gamma * exp(-beta*diff.dot(diff));
}
else
upW.at<double>(y,x) = 0;
if( x+1<img.cols && y-1>=0 ) // upright
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y-1,x+1);
uprightW.at<double>(y,x) = gammaDivSqrt2 * exp(-beta*diff.dot(diff));
}
else
uprightW.at<double>(y,x) = 0;
}
}
}
//检查mask的正确性。mask为通过用户交互或者程序设定的，它是和图像大小一样的单通道灰度图，
//每个像素只能取GC_BGD or GC_FGD or GC_PR_BGD or GC_PR_FGD 四种枚举值，分别表示该像素
//（用户或者程序指定）属于背景、前景、可能为背景或者可能为前景像素。具体的参考：
//ICCV2001“Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images”
//Yuri Y. Boykov Marie-Pierre Jolly
/*
Check size, type and element values of mask matrix.
*/
static void checkMask( const Mat& img, const Mat& mask )
{
if( mask.empty() )
CV_Error( CV_StsBadArg, "mask is empty" );
if( mask.type() != CV_8UC1 )
CV_Error( CV_StsBadArg, "mask must have CV_8UC1 type" );
if( mask.cols != img.cols || mask.rows != img.rows )
CV_Error( CV_StsBadArg, "mask must have as many rows and cols as img" );
for( int y = 0; y < mask.rows; y++ )
{
for( int x = 0; x < mask.cols; x++ )
{
uchar val = mask.at<uchar>(y,x);
if( val!=GC_BGD && val!=GC_FGD && val!=GC_PR_BGD && val!=GC_PR_FGD )
CV_Error( CV_StsBadArg, "mask element value must be equel"
"GC_BGD or GC_FGD or GC_PR_BGD or GC_PR_FGD" );
}
}
}
//通过用户框选目标rect来创建mask，rect外的全部作为背景，设置为GC_BGD，
//rect内的设置为 GC_PR_FGD（可能为前景）
/*
Initialize mask using rectangular.
*/
static void initMaskWithRect( Mat& mask, Size imgSize, Rect rect )
{
mask.create( imgSize, CV_8UC1 );
mask.setTo( GC_BGD );
rect.x = max(0, rect.x);
rect.y = max(0, rect.y);
rect.width = min(rect.width, imgSize.width-rect.x);
rect.height = min(rect.height, imgSize.height-rect.y);
(mask(rect)).setTo( Scalar(GC_PR_FGD) );
}
//通过k-means算法来初始化背景GMM和前景GMM模型
/*
Initialize GMM background and foreground models using kmeans algorithm.
*/
static void initGMMs( const Mat& img, const Mat& mask, GMM& bgdGMM, GMM& fgdGMM )
{
const int kMeansItCount = 10; //迭代次数
const int kMeansType = KMEANS_PP_CENTERS; //Use kmeans++ center initialization by Arthur and Vassilvitskii
Mat bgdLabels, fgdLabels; //记录背景和前景的像素样本集中每个像素对应GMM的哪个高斯模型，论文中的kn
vector<Vec3f> bgdSamples, fgdSamples; //背景和前景的像素样本集
Point p;
for( p.y = 0; p.y < img.rows; p.y++ )
{
for( p.x = 0; p.x < img.cols; p.x++ )
{
//mask中标记为GC_BGD和GC_PR_BGD的像素都作为背景的样本像素
if( mask.at<uchar>(p) == GC_BGD || mask.at<uchar>(p) == GC_PR_BGD )
bgdSamples.push_back( (Vec3f)img.at<Vec3b>(p) );
else // GC_FGD | GC_PR_FGD
fgdSamples.push_back( (Vec3f)img.at<Vec3b>(p) );
}
}
CV_Assert( !bgdSamples.empty() && !fgdSamples.empty() );
//kmeans中参数_bgdSamples为：每行一个样本
//kmeans的输出为bgdLabels，里面保存的是输入样本集中每一个样本对应的类标签（样本聚为componentsCount类后）
Mat _bgdSamples( (int)bgdSamples.size(), 3, CV_32FC1, &bgdSamples[0][0] );
kmeans( _bgdSamples, GMM::componentsCount, bgdLabels,
TermCriteria( CV_TERMCRIT_ITER, kMeansItCount, 0.0), 0, kMeansType );
Mat _fgdSamples( (int)fgdSamples.size(), 3, CV_32FC1, &fgdSamples[0][0] );
kmeans( _fgdSamples, GMM::componentsCount, fgdLabels,
TermCriteria( CV_TERMCRIT_ITER, kMeansItCount, 0.0), 0, kMeansType );
//经过上面的步骤后，每个像素所属的高斯模型就确定的了，那么就可以估计GMM中每个高斯模型的参数了。
bgdGMM.initLearning();
for( int i = 0; i < (int)bgdSamples.size(); i++ )
bgdGMM.addSample( bgdLabels.at<int>(i,0), bgdSamples[i] );
bgdGMM.endLearning();
fgdGMM.initLearning();
for( int i = 0; i < (int)fgdSamples.size(); i++ )
fgdGMM.addSample( fgdLabels.at<int>(i,0), fgdSamples[i] );
fgdGMM.endLearning();
}
//论文中：迭代最小化算法step 1：为每个像素分配GMM中所属的高斯模型，kn保存在Mat compIdxs中
/*
Assign GMMs components for each pixel.
*/
static void assignGMMsComponents( const Mat& img, const Mat& mask, const GMM& bgdGMM,
const GMM& fgdGMM, Mat& compIdxs )
{
Point p;
for( p.y = 0; p.y < img.rows; p.y++ )
{
for( p.x = 0; p.x < img.cols; p.x++ )
{
Vec3d color = img.at<Vec3b>(p);
//通过mask来判断该像素属于背景像素还是前景像素，再判断它属于前景或者背景GMM中的哪个高斯分量
compIdxs.at<int>(p) = mask.at<uchar>(p) == GC_BGD || mask.at<uchar>(p) == GC_PR_BGD ?
bgdGMM.whichComponent(color) : fgdGMM.whichComponent(color);
}
}
}
//论文中：迭代最小化算法step 2：从每个高斯模型的像素样本集中学习每个高斯模型的参数
/*
Learn GMMs parameters.
*/
static void learnGMMs( const Mat& img, const Mat& mask, const Mat& compIdxs, GMM& bgdGMM, GMM& fgdGMM )
{
bgdGMM.initLearning();
fgdGMM.initLearning();
Point p;
for( int ci = 0; ci < GMM::componentsCount; ci++ )
{
for( p.y = 0; p.y < img.rows; p.y++ )
{
for( p.x = 0; p.x < img.cols; p.x++ )
{
if( compIdxs.at<int>(p) == ci )
{
if( mask.at<uchar>(p) == GC_BGD || mask.at<uchar>(p) == GC_PR_BGD )
bgdGMM.addSample( ci, img.at<Vec3b>(p) );
else
fgdGMM.addSample( ci, img.at<Vec3b>(p) );
}
}
}
}
bgdGMM.endLearning();
fgdGMM.endLearning();
}
//通过计算得到的能量项构建图，图的顶点为像素点，图的边由两部分构成，
//一类边是：每个顶点与Sink汇点t（代表背景）和源点Source（代表前景）连接的边，
//这类边的权值通过Gibbs能量项的第一项能量项来表示。
//另一类边是：每个顶点与其邻域顶点连接的边，这类边的权值通过Gibbs能量项的第二项能量项来表示。
/*
Construct GCGraph
*/
static void constructGCGraph( const Mat& img, const Mat& mask, const GMM& bgdGMM, const GMM& fgdGMM, double lambda,
const Mat& leftW, const Mat& upleftW, const Mat& upW, const Mat& uprightW,
GCGraph<double>& graph )
{
int vtxCount = img.cols*img.rows; //顶点数，每一个像素是一个顶点
int edgeCount = 2*(4*vtxCount - 3*(img.cols + img.rows) + 2); //边数，需要考虑图边界的边的缺失
//通过顶点数和边数创建图。这些类型声明和函数定义请参考gcgraph.hpp
graph.create(vtxCount, edgeCount);
Point p;
for( p.y = 0; p.y < img.rows; p.y++ )
{
for( p.x = 0; p.x < img.cols; p.x++)
{
// add node
int vtxIdx = graph.addVtx(); //返回这个顶点在图中的索引
Vec3b color = img.at<Vec3b>(p);
// set t-weights
//计算每个顶点与Sink汇点t（代表背景）和源点Source（代表前景）连接的权值。
//也即计算Gibbs能量（每一个像素点作为背景像素或者前景像素）的第一个能量项
double fromSource, toSink;
if( mask.at<uchar>(p) == GC_PR_BGD || mask.at<uchar>(p) == GC_PR_FGD )
{
//对每一个像素计算其作为背景像素或者前景像素的第一个能量项，作为分别与t和s点的连接权值
fromSource = -log( bgdGMM(color) );
toSink = -log( fgdGMM(color) );
}
else if( mask.at<uchar>(p) == GC_BGD )
{
//对于确定为背景的像素点，它与Source点（前景）的连接为0，与Sink点的连接为lambda
fromSource = 0;
toSink = lambda;
}
else // GC_FGD
{
fromSource = lambda;
toSink = 0;
}
//设置该顶点vtxIdx分别与Source点和Sink点的连接权值
graph.addTermWeights( vtxIdx, fromSource, toSink );
// set n-weights n-links
//计算两个邻域顶点之间连接的权值。
//也即计算Gibbs能量的第二个能量项（平滑项）
if( p.x>0 )
{
double w = leftW.at<double>(p);
graph.addEdges( vtxIdx, vtxIdx-1, w, w );
}
if( p.x>0 && p.y>0 )
{
double w = upleftW.at<double>(p);
graph.addEdges( vtxIdx, vtxIdx-img.cols-1, w, w );
}
if( p.y>0 )
{
double w = upW.at<double>(p);
graph.addEdges( vtxIdx, vtxIdx-img.cols, w, w );
}
if( p.x<img.cols-1 && p.y>0 )
{
double w = uprightW.at<double>(p);
graph.addEdges( vtxIdx, vtxIdx-img.cols+1, w, w );
}
}
}
}
//论文中：迭代最小化算法step 3：分割估计：最小割或者最大流算法
/*
Estimate segmentation using MaxFlow algorithm
*/
static void estimateSegmentation( GCGraph<double>& graph, Mat& mask )
{
//通过最大流算法确定图的最小割，也即完成图像的分割
graph.maxFlow();
Point p;
for( p.y = 0; p.y < mask.rows; p.y++ )
{
for( p.x = 0; p.x < mask.cols; p.x++ )
{
//通过图分割的结果来更新mask，即最后的图像分割结果。注意的是，永远都
//不会更新用户指定为背景或者前景的像素
if( mask.at<uchar>(p) == GC_PR_BGD || mask.at<uchar>(p) == GC_PR_FGD )
{
if( graph.inSourceSegment( p.y*mask.cols+p.x /*vertex index*/ ) )
mask.at<uchar>(p) = GC_PR_FGD;
else
mask.at<uchar>(p) = GC_PR_BGD;
}
}
}
}
//最后的成果：提供给外界使用的伟大的API：grabCut
/*
****参数说明：
img——待分割的源图像，必须是8位3通道（CV_8UC3）图像，在处理的过程中不会被修改；
mask——掩码图像，如果使用掩码进行初始化，那么mask保存初始化掩码信息；在执行分割
的时候，也可以将用户交互所设定的前景与背景保存到mask中，然后再传入grabCut函
数；在处理结束之后，mask中会保存结果。mask只能取以下四种值：
GCD_BGD（=0），背景；
GCD_FGD（=1），前景；
GCD_PR_BGD（=2），可能的背景；
GCD_PR_FGD（=3），可能的前景。
如果没有手工标记GCD_BGD或者GCD_FGD，那么结果只会有GCD_PR_BGD或GCD_PR_FGD；
rect——用于限定需要进行分割的图像范围，只有该矩形窗口内的图像部分才被处理；
bgdModel——背景模型，如果为null，函数内部会自动创建一个bgdModel；bgdModel必须是
单通道浮点型（CV_32FC1）图像，且行数只能为1，列数只能为13x5；
fgdModel——前景模型，如果为null，函数内部会自动创建一个fgdModel；fgdModel必须是
单通道浮点型（CV_32FC1）图像，且行数只能为1，列数只能为13x5；
iterCount——迭代次数，必须大于0；
mode——用于指示grabCut函数进行什么操作，可选的值有：
GC_INIT_WITH_RECT（=0），用矩形窗初始化GrabCut；
GC_INIT_WITH_MASK（=1），用掩码图像初始化GrabCut；
GC_EVAL（=2），执行分割。
*/
void cv::grabCut( InputArray _img, InputOutputArray _mask, Rect rect,
InputOutputArray _bgdModel, InputOutputArray _fgdModel,
int iterCount, int mode )
{
Mat img = _img.getMat();
Mat& mask = _mask.getMatRef();
Mat& bgdModel = _bgdModel.getMatRef();
Mat& fgdModel = _fgdModel.getMatRef();
if( img.empty() )
CV_Error( CV_StsBadArg, "image is empty" );
if( img.type() != CV_8UC3 )
CV_Error( CV_StsBadArg, "image mush have CV_8UC3 type" );
GMM bgdGMM( bgdModel ), fgdGMM( fgdModel );
Mat compIdxs( img.size(), CV_32SC1 );
if( mode == GC_INIT_WITH_RECT || mode == GC_INIT_WITH_MASK )
{
if( mode == GC_INIT_WITH_RECT )
initMaskWithRect( mask, img.size(), rect );
else // flag == GC_INIT_WITH_MASK
checkMask( img, mask );
initGMMs( img, mask, bgdGMM, fgdGMM );
}
if( iterCount <= 0)
return;
if( mode == GC_EVAL )
checkMask( img, mask );
const double gamma = 50;
const double lambda = 9*gamma;
const double beta = calcBeta( img );
Mat leftW, upleftW, upW, uprightW;
calcNWeights( img, leftW, upleftW, upW, uprightW, beta, gamma );
for( int i = 0; i < iterCount; i++ )
{
GCGraph<double> graph;
assignGMMsComponents( img, mask, bgdGMM, fgdGMM, compIdxs );
learnGMMs( img, mask, compIdxs, bgdGMM, fgdGMM );
constructGCGraph(img, mask, bgdGMM, fgdGMM, lambda, leftW, upleftW, upW, uprightW, graph );
estimateSegmentation( graph, mask );
}
}