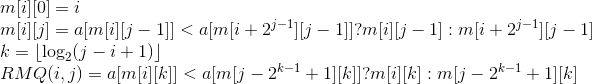Range Minimum Query(RMQ)

对于长度为n的数列A，回答若干询问RMQ(A,i,j)(i,j<=n)，返回数列A中下标在i,j里的最小(大）值，也就是说，RMQ问题是指求区间最值的问题。

1.Sparse Table(ST)算法

动规：M[i][j]是以i开始，长度为2^j的子数组的最小值的索引。

#include<iostream> 
#include<cmath>
using namespace std;    
const int n=10;

void pretreatment(int a[n],int m[][n])
{
    int i,j;
    for(i=0;i<n;++i)m[i][0]=i;
    for(j=1;1<<j<=n;++j)
    {
        for(i=0;i<=n-(1<<j);++i)
        {
            m[i][j]=a[m[i][j-1]]<a[m[i+(1<<(j-1))][j-1]]?m[i][j-1]:m[i+(1<<(j-1))][j-1];
        }
    }
}

int RMQ(int a[],int m[][n],int i,int j)
{
    int k=int(log(double(j-i+1))/log(double(2)));
    return a[m[i][k]]<a[m[j-(1<<k)+1][k]]?m[i][k]:m[j-(1<<k)+1][k];
}

int main()  
{   
    int a[n]={2,4,3,1,6,7,8,9,1,7};
    int m[n][n];
    pretreatment(a,m);
    cout<<RMQ(a,m,2,7)<<endl;
    return 0;  
}