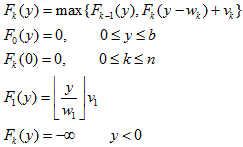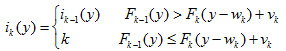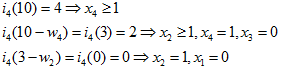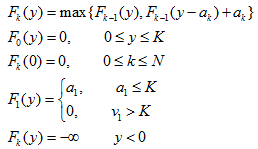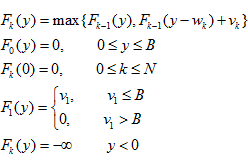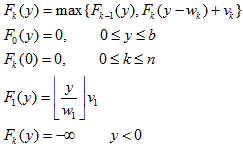背包问题

研究生课程系列文章参见索引《在信科的那些课》

题目

一个旅行者准备随身携带一个背包，可以放入背包的物品有n种，每种物品的重量和价值分别为wj, vj . 如果背包的最大重量限制是b, 怎样选择放入背包的物品以使得背包的价值最大?

目标函数：

约束条件：

算法设计

设Fk(y) 表示只允许装前k 种物品,背包总重不超过y 时背包的最大价值。Fk(y)有两种情况：不装第k件物品或至少装1件第k种物品。

如果不装第k件物品，那么只能用前k-1件物品装入背包，背包的限制重量仍为y，所以最大价值是Fk-1(y)；

如果装1件第k件物品，那么装入的第k件物品价值为vk，重量为wk，剩下的物品仍要在前k件里选择（因为每件物品可以装多件，如果只能装1件就是在前k-1件里选择）。于是问题规约为背包限制重量y-wk的情况下前k件物品取得最大价值，即Fk(y-wk)+vk。 递推方程与边界条件：

上式初值比较多，F0(y)是不装物品的最大价值；F1(y)是只能装第一件物品时，最多装|_y/w1_|件；递推式Fk(y-wk)，y-wk有可能得到负值，即不能再装物品，所以设置最小数以保证在优化问题中淘汰这种情况。

算法实现

标记函数：实现是需要一个ik(y)记录优化函数Fk(y)用到物品的最大标号。计算Fk(y)时，如果Fk-1(y)>Fk(y-wk)+vk，即没有加入第k件物品，ik(y)即为Fk-1(y)的物品最大标号；反正，加入第k件物品，ik(y)记为k。标记函数递归关系：

代码如下：

void Knapsack(int v[N],int w[N],int F[][B+1],int tagi[][B+1]){
    for(int k=0;k<=N;k++){
        F[k][0]=0;
        tagi[k][0]=0;
    }
    for(int y=0;y<=B;y++){
        F[0][y]=0;
        F[1][y]=(int)(y/w[0])*v[0];//只能装第一件物品时
        tagi[0][y]=0;
    }

    for(int k=1;k<=N;k++){
        for(int y=1;y<=B;y++){
            if(y-w[k-1]<0){
                F[k][y]=F[k-1][y];
                tagi[k][y]=tagi[k-1][y];
            }
            else{
                //允许装入k件物品，价值的两种情况：
                //不装第k件物品或至少装1件第k件物品
                F[k][y]=F[k-1][y]>F[k][y-w[k-1]]+v[k-1] ? F[k-1][y]:(F[k][y-w[k-1]]+v[k-1]);
                tagi[k][y]=F[k-1][y]>F[k][y-w[k-1]]+v[k-1]?tagi[k-1][y]:k;
            }
        }
    }
}

实例及解的追踪

试验下面的例子：

v1=1，v2=3，v3=5，v4=9，w1=2，w2=3，w3=4，w4=7，b=10

运行结果如下图：

我们需要在标记函数ik(y)中把实际解，及每个物品分别装入多少件追踪出来。

由最后i4(10)开始，i4(10)=4，表示此时第4件物品至少装入1件，占用重量w4=7，于是背包剩余重量为10-7=3；继续查询i4(3)，由i4(3)=2，表示剩余物品最大标号为2，第2件物品至少装入1件。剩余重量为0，即不能再装入物品。用公式表示 追踪解的过程：

根据实例，可以理出追踪解的思路，代码如下：

void TrackSolution(int v[N],int w[N],int tagi[][B+1]){
    //x[i-1]标记第i件物品的件数
    int x[N];
    for(int i=0;i<N;i++)
        x[i]=0;
    int y=B,j=tagi[N][B];
    while (tagi[j][y]!=0){
         j=tagi[j][y];
        //标记函数最下角ik(y)标记的物品取一件
        x[j-1]=1;
        y=y-w[j-1];
        while (tagi[j][y]==j){
            y=y-w[j];
            x[j-1]=x[j-1]+1;
        }
    }
}

运行结果：

其他题目

背包问题是很经典的动态规划问题，很多问题都是背包的变种，比如下面两个题目：

• 设P是一台Internet上的Web服务器。T={1,2,...,n}是n个下载请求集合，ai为正整数，表示下载请求i所申请的带宽，已知服务器的最大带宽是正整数K。我们的目标是使带宽得到最大限度的利用，即确定T的一个子集S，使得，且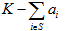达到最小。设计一个算法求服务器下载问题。
• 设有n项任务，加工时间分别表示为正整数t1，t2，...，tn。现有2台同样的机器，从0时刻可以安排对这些任务的加工，知道T时刻所有任务完成，总加工时间为T。设计算法使得总加工时间T最小的调度方案。

第一个题目其实就是0-1背包问题，即看做价值和重量相等（都为ai）的物品装入背包，每件物品最多选1件，总重不能超过K，总价值最大的问题。设Fk(y)表示只允许前k个下载请求，最大带宽不超过y时利用最大限度的带宽数。 递推关系和边界条件如下：

注意0-1背包和背包问题的递推关系主要区别是：当选择第k件物品时，Fk(y)表示为Fk-1(y-wk)+vk，而非Fk(y-wk)+vk，即只能在前k-1件物品里继续选择。另外F1(y)的边界函数也不同。

至于第二个题目，其实就是使得一条加工线上的加工时间不超过T/2时加工时间尽可能大的问题，和第一个问题是一样的。

代码下载： http://download.csdn.net/detail/xiaowei_cqu/4775367

参考资料：屈婉玲 刘田等 《算法设计与分析》

研究生课程系列文章参见索引《在信科的那些课》

之前整理了屈奶奶讲的背包问题，感谢cyh24童鞋留言，传我一份武林秘籍《背包问题九讲》，实践了一下文档里对空间复杂度的改进。

0-1背包问题

通过之前的分析，Fk(y) 表示只允许装前k 种物品,背包总重不超过y 时背包的最大价值。得到0-1背包的递推公式和边界条件：

对空间的优化主要在Fk(y)，原本我们用两个循环实现：

for(int k=1;k<=N;k++){
    for(int y=1;y<=B;y++){
        if(y-w[k-1]<0){
            F[k][y]=F[k-1][y];
            tagi[k][y]=tagi[k-1][y];
        }
        else{
            //允许装入k件物品，价值的两种情况：
            //不装第k件物品或至少装1件第k件物品
            F[k][y]=F[k-1][y]>F[k][y-w[k-1]]+v[k-1] ? F[k-1][y]:(F[k][y-w[k-1]]+v[k-1]);
            tagi[k][y]=F[k-1][y]>F[k][y-w[k-1]]+v[k-1]?tagi[k-1][y]:k;
        }
    }
}

实际并一定不需要F[N][B]的空间，如果内层循环以B...0递推，即下面的形式：

for(int k=1;k<=N;k++){
    for(int y=B;y>0;y--){
        F[y]=max{F[y],F[y-w[i]]+v[i]};
    }
}

因为是以B...0倒序递推，则F[y]此时就是F[k-1][y]的值,而F[y-w]还未改变，仍为F[k-1][y-w]的值。因此可以用一维数组存储原来的优化函数信息。代码如下：

void ZeroOnePack(int F[],int tagi[],int v, int w,int k){
    for(int i=B;i>0;i--){
        if(i-w>=0&&F[i]<=(F[i-w]+v)){
            F[i]=F[i-w]+v;
            tagi[i]=k;
        }
    }
}

完全背包问题

再看完全背包问题，即每个物品有无限件，不限每个物品装入的个数。得到递推关系和边界条件：

递归公式最主要的区别是Fk(y-wk)+vk，而非原来的Fk-1(y-wk)+vk，即物品可以在前k件中继续挑选。用一维数组时希望此时F[y]的数值即为F[k-1][y]的数值，而F[y-w]的数值为改变之后的F[k-1][y-w]的数值。因此我们可以用顺序0...B（而非逆序B...0）实现：

for(int k=1;k<=N;k++){
    for(int y=0;y>B;y++){
        F[y]=max{F[y],F[y-w[i]]+v[i]};
    }
}

具体代码如下：

void CompletePack(int F[],int tagi[],int v, int w,int k){

    //F[i]=F[i]>(F[i-w]+v)?F[i]:(F[i-w]+v);
    //tagi=F[i]>(F[i-w]+v)?tagi:tagi+1;

    for(int i=1;i<=B;i++){
        if(i-w>=0&&F[i]<=(F[i-w]+v)){
            F[i]=F[i-w]+v;
            tagi[i]=k;
        }
    }
}

测试用例

前面是0-1背包和完全背包的内层循环，还需要一个外层循环调用：

void Knapsack(int F[],int tagi[][B+1],int v[], int w[]){
    for(int i=0;i<B+1;i++){
        F[i]=tagi[0][i]=0;
    }
    for(int i=0;i<N+1;i++)
        tagi[i][0]=0;

    for(int i=0;i<N;i++){
        for(int j=0;j<B+1;j++)
            tagi[i+1][j]=tagi[i][j];
        //0-1背包
        ZeroOnePack(F,tagi[i+1],v[i],w[i],i+1);
        //完全背包
        //CompletePack(F,tagi[i+1],v[i],w[i],i+1);
    }
}

还有 之前文章的例子来测试，输出结果：

代码及文档下载： http://download.csdn.net/detail/xiaowei_cqu/4787977

参考资料：dd_engi等 《背包问题九讲》