poj 1191 棋盘分割（记忆化搜索/动态规划）

程序设计实习递归练习 poj 1191 棋盘分割（记忆化搜索/动态规划）
总时间限制: 1000ms 内存限制: 65536kB

描述
将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

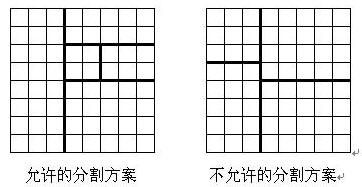
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。
均方差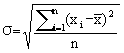，其中平均值=，xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n，求出O’的最小值。

输入
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出
仅一个数，为O’（四舍五入精确到小数点后三位）。

样例输入
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

样例输出
1.633

来源
Noi 99

把方差展开，就会发现只需要令每一块平方和最小，这样一来这个问题就变成常规问题了。
这个题目思路一旦想明白比较简单，但是一些细节处理还是比较麻烦的。思路无非是一开始想到搜索，很快发现子问题重叠度很高，就用记忆化搜索。另一方面，也可以用动态规划的思路来想，一个是递归一个是递推，思路几乎一样，实现起来略有差别。我个人比较喜欢递归的方式，因为记忆化搜索实现框架非常简单，不必像递推实现的动态规划一样自己去安排合理的递推顺序，当然后者代码更高效一些。所以也收录了后者版本的网上的代码作为version 2代码供学习。
但是，本题在框架确定情况下还有两个小细节：
1.一个是搜索的边界问题，仔细思考后可以想明白，但是务必仔细思考。
2.注意！不要在openjudge上使用long double数据类型，不要以为精度越高越好，这里double已经可以了就不要用long double了，因为在poj上似乎long double用printf的”%llf”输出是会莫名其妙WA！我已经WA了很多回了，后来看别人的文章才意识到这个问题。

我做过程本题十分辛酸，时间跨度极大，期间错误犯过很多，调试了很久，因为WA，TLE了太多次，贴一个提交表纪念一下。另外，贴的两个版本代码在#define TEST模式下可以用来测试。其中version 2来自网络，用递推式动态规划实现，vesion 1为我自己的版本，记忆化搜索实现动态规划。

poj提交记录
- 17 Accepted· 05-18
- 16 Accepted 05-18 （version 1 AC）
- 15 Wrong Answer 05-18 （version 1 用了long double错误！）
- 14 Wrong Answer 05-18
- 13 Wrong Answer 05-18
- 12 Accepted 05-18 （version 2测试）
- 11 Wrong Answer 05-18 （version 1边界条件错误）
- 10 Wrong Answer 05-18
- 9 Wrong Answer 05-18
- 8 Wrong Answer 05-18
- 7 Wrong Answer 05-16
- 6 Wrong Answer 05-16
- 5 Wrong Answer 04-29
- 4 Wrong Answer 04-29
- 3 Time Limit Exceeded 04-20（搜索超时）
- 2 Wrong Answer 04-20 （没搜索完整）
- 1 Wrong Answer 04-20 （没搜索完整）

version 1

#include<stdio.h>
#include<math.h>
#include<memory.h>
#include<iostream>

#define TEST
#undef TEST

typedef long long _type;

int map[9][9],sum[9][9];
int n;
_type min[9][9][9][9][15];

void  readIn()
{
    memset(map,0,sizeof(map));
    memset(sum,0,sizeof(sum));
    memset(min,0,sizeof(min));
    scanf("%d",&n);
    for (int i=1;i<=8;i++)
        for (int j=1;j<=8;j++)
            scanf("%d",&map[i][j]);
    for (int i=1;i<=8;i++)
        for (int j=1;j<=8;j++)
            sum[i][j]=map[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];
    for (int iu=1;iu<=8;iu++)
        for (int id=iu;id<=8;id++)
            for (int jl=1;jl<=8;jl++)
                for (int jr=jl;jr<=8;jr++)
                    min[iu][id][jl][jr][1]=(_type)
         (sum[id][jr]+sum[iu-1][jl-1]-sum[id][jl-1]-sum[iu-1][jr])*
         (sum[id][jr]+sum[iu-1][jl-1]-sum[id][jl-1]-sum[iu-1][jr]);
    return;
}

_type f(int iu,int id,int jl,int jr,int plane)
{
    if (iu>id || jl>jr || id-iu+jr-jl+1<plane)
        return (_type)0x20000000;
    if (min[iu][id][jl][jr][plane] || plane==1)
        return min[iu][id][jl][jr][plane];
    _type temp=(_type)0x20000000;
    for (int i=iu;i<id;i++)
        if (f(iu,i,jl,jr,1)+f(i+1,id,jl,jr,plane-1)<temp)
            temp=f(iu,i,jl,jr,1)+f(i+1,id,jl,jr,plane-1);
    for (int i=iu;i<id;i++)
        if (f(iu,i,jl,jr,plane-1)+f(i+1,id,jl,jr,1)<temp)
            temp=f(iu,i,jl,jr,plane-1)+f(i+1,id,jl,jr,1);
    for (int j=jl;j<jr;j++)
        if (f(iu,id,jl,j,1)+f(iu,id,j+1,jr,plane-1)<temp)
            temp=f(iu,id,jl,j,1)+f(iu,id,j+1,jr,plane-1);
    for (int j=jl;j<jr;j++)
        if (f(iu,id,jl,j,plane-1)+f(iu,id,j+1,jr,1)<temp)
            temp=f(iu,id,jl,j,plane-1)+f(iu,id,j+1,jr,1);
    min[iu][id][jl][jr][plane]=temp;
    return temp;
}

int main()
{
    #ifdef TEST
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    while (std::cin.peek()!=EOF){
    memset(min,0,sizeof(min));
    #endif
    readIn();
    printf("%.3lf\n",sqrt(f(1,8,1,8,n)/(n*1.0)-(sum[8][8]*sum[8][8])/(n*n*1.0)));
    #ifdef TEST
    }
    #endif
    return 0;
}

version 2

#include <iostream>
#include <cstdio>
#include <cmath>
#include <iomanip>
#include <memory.h>
#define TEST

using namespace std;

int data[9][9];
int sum[9][9];
double dp[14][9][9][9][9];

//返回左上角坐标(x1,y1)到右下角坐标(x2,y2)区域的棋盘的分值和平方 
double count(int x1, int y1, int x2, int y2)
{
    double ans = (double)(sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]);

    return ans*ans;
}

int main()
{
    #ifdef TEST
    freopen("input.txt","r",stdin);
    freopen("output(anwser).txt","w",stdout);
    while (cin.peek()!=EOF){
    memset(dp,0,sizeof(dp));
    #endif
    int n, total=0;
    //输入数据 
    cin>>n;
    for(int i=1; i<=8; ++i)
      for(int j=1; j<=8; ++j)
      {
            cin>>data[i][j];
            //sum[i][j]表示棋盘(1,1)到(i,j)区域的累计分值 
            sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + data[i][j];
            //total表示整个棋盘的分值之和 
            total += data[i][j];
        }

    //初始化dp数组 
    for(int x1=1; x1<=8; ++x1)
     for(int y1=1; y1<=8; ++y1)
      for(int x2=x1; x2<=8; ++x2)
          for(int y2=y1; y2<=8; ++y2)
             dp[0][x1][y1][x2][y2] = count(x1,y1,x2,y2);

    //自底向上计算dp数据 
    for(int k=1; k<n; ++k)
     for(int x1=1; x1<=8; ++x1)
      for(int y1=1; y1<=8; ++y1)
       for(int x2=x1; x2<=8; ++x2)
          for(int y2=y1; y2<=8; ++y2)
          {
                int t;
                dp[k][x1][y1][x2][y2] = (double)(1<<30);
                for(t=x1; t<x2; ++t)
                {
                    dp[k][x1][y1][x2][y2] = min(dp[k][x1][y1][x2][y2], dp[0][x1][y1][t][y2]+dp[k-1][t+1][y1][x2][y2]);
                    dp[k][x1][y1][x2][y2] = min(dp[k][x1][y1][x2][y2], dp[k-1][x1][y1][t][y2]+dp[0][t+1][y1][x2][y2]);
                }

                for(t=y1; t<y2; ++t)
                {
                    dp[k][x1][y1][x2][y2] = min(dp[k][x1][y1][x2][y2], dp[0][x1][y1][x2][t]+dp[k-1][x1][t+1][x2][y2]);
                    dp[k][x1][y1][x2][y2] = min(dp[k][x1][y1][x2][y2], dp[k-1][x1][y1][x2][t]+dp[0][x1][t+1][x2][y2]);
                }
            }

    //计算方差平方 
    double ans = dp[n-1][1][1][8][8]*1.0/n - ((double)total*1.0/n)*((double)total*1.0/n); 

    //输出方差,精确到小数点后三位 
    cout<<setprecision(3)<<fixed<<sqrt(ans)<<endl;
    #ifdef TEST
    }
    #endif 
    return 0;
}