笔试面试题目6
1. 一串无序的N个数,a1, a2, a3, a4, ... , an,经过简单的操作之后,形成另外一个串,包含这些数字,b1, b2, b3, b4, ..., bn,并且要求 b1<= b2 >= b3 <= b4 >= ...
地找出合适的a和b。
可以先对数组b 进行排序,排序完成之后,遍历数组a[]中元素,使用二分搜索的方法对数组b[]中的元素进行查找
找到合适的元素。
4. 给定两个已经排好序的实数数组a[]和b[],如果对两个数字组合并排序会形成一个新的数组,这个数组会有一个中位数(排在数组中间的那个数),要求使用a[]和b[]找到那个中位数。(答案转自: http://blog.csdn.net/zcsylj/article/details/6802062)
第一题:假设两个有序数组(已经各自排序完成了)长度相等,试写函数找出两个数组合并后的中位数。
解析: 这个题目看起来非常简单。第一题的话: 假设数组长度为n, 那么我就把数组1和数组2直接合并,然后再直接找到中间元素。对于这样的方案,第一题和第一题就没有什么区别了。这样的话时间复杂度就是O(n)。通常在这样的情况下,那些mentor类型的达人就会循循善诱道:“你还有更好的办法吗:)” 如果比线性更高效,直接能想到的就是对数了O(log(n)),这个时间复杂度在这里可能吗?当然还是可能的。来继续看看下面的分析。先找来了一个图(自己画的,简陋了点)
我们先来分析看看:想到对数的效率,首先想到的就是二分查找,对于这个题目二分查找的意义在哪里呢?
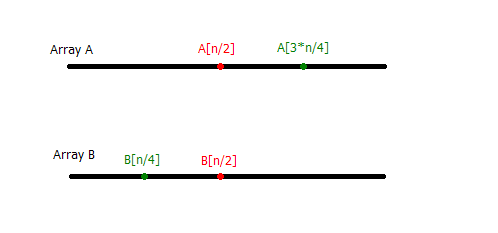
我们找到了A[n/2]和B[n/2]来比较,
如果他们相等,那样的话,我们的搜索结束了,因为答案已经找到了A[n/2]就肯定是排序后的中位数了。
如果我们发现 B[n/2]>A[n/2],说明什么,这个数字应该在 A[n/2]->A[n]这个序列里面,或者在 B[1]-B[n/4]这里面。或者,这里的或者是很重要的,我们可以说,我们已经成功的把问题变成了在排序完成的数组A[n/2]-A[n]和B[0]-B[n/2]里面找到合并以后的中位数,显然递归是个不错的选择了。
类似的,如果B[n/2]<A[n/2]呢?显然就是在A[0]-A[n/2]和B[n/2]-B[n]里面寻找了。
a.如果A[n/2] == B[m/2],那么很显然,我们的讨论结束了。A[n/2]就已经是中位数,这个和他们各自的长度是奇数或者偶数无关。
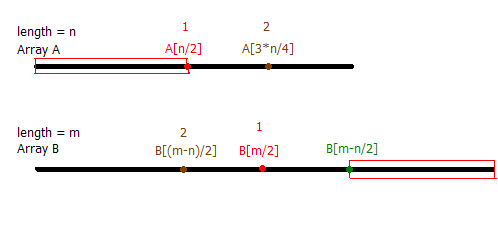
b.如果A[n/2] < B[m/2],那么,我们可以知道这个中位数肯定不在[A[0],A[n/2])这个区间内,同时也不在[B[m/2],B[m]]这个区间里面。这个时候,我们不能冲动地把[A[0],A[n/2])和[B[m/2],B[m]]全部扔掉。我们只需要把[B[m-n/2],B[m]]和[A[0],A[n/2])扔掉就可以了。(如图所示的红色线框),这样我们就把我们的问题成功转换成了如何在A[n/2]->A[n]这个长度为n/2的数组和B[1]-B[m-n/2]这个长度为m-n/2的数组里面找中位数了。问题复杂度即可下降了。
c.只剩下A[n/2] > B[m/2],和b类似的,我们可以把A[n/2]->A[n]这块以及B[1]->B[n/2]这块扔掉了就行,然后继续递归。
我们也可以写下如下的代码:
1-1 1-2 1-3 1-4 1-5 1-6
2-1 2-2 2-3 2-4 2-5 2-6
3-1 3-2 3-3 3-4 3-5 3-6
4-1 4-2 4-3 4-4 4-5 4-6
5-1 5-2 5-3 5-4 5-5 5-6
6-1 6-2 6-3 6-4 6-5 6-6
由此,由上图我们可以预见,第一轮中36匹马分为6组,每一组6匹马,然后每一组跑一次。各组得出名次。
第二轮取出每一组的第一名,跑一场,得到一个排名,然后取出前三名。将前三名对应的组的马挑选出来三匹再赛,挑选规则:
下图中所有图示的红线均表示剩下两个杯子的时候的试摔位置,当杯子破碎后,也就是只剩下一个杯子的时候,只需要从已知范围的最底层向已知范围的最高层逐层试摔。
当有一层的时候,需要一次试摔。
当有两层的时候,需要两次试摔。
当需要三层时候,首先讨论是否可以通过两次试摔完成,可以发现可以,方法如图。
当需要四层时候,首先讨论是否可以通过两次试摔完成,可以发现已经不行,因此至少需要三次试摔。
当需要五层时候,首先讨论是否可以通过小于等于三次试摔完成,如果不行则讨论最多四次试摔的情况。依次类推,如下图:

因此,当有100层的时候,最多需要n次试摔,使得 n+(n-1)+(n-2)+...+1 >= 100,然后对n上取整,因此n=14。最差情况需要14次试摔。试摔方法为:第一次在14层扔,如果没破,在27层(14+13)继续扔,不破在39层(27+12)继续扔,依次类推。如果破了,剩下一个杯子,从已知范围的最底层向已知范围的最高层逐层试摔。
7. 写快速排序算法
问其中一个人一个常识性的问题,例如你是男的吗?从而确定另外一个人是说谎还是说真话,即可得到通往A的路
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void SortData( int data[], int n)
{
for( int i = 0; i < n-1; i++)
{
if(i % 2 == 0) // 偶数
{
if(data[i] > data[i+1])
{
int tmp = data[i];
data[i] = data[i+1];
data[i+1] = tmp;
}
}
else // 奇数
{
if(data[i] < data[i+1])
{
int tmp = data[i];
data[i] = data[i+1];
data[i+1] = tmp;
}
}
}
}
int main()
{
int data[10];
for( int i = 0; i < 10; i++)
{
data[i] = i+1;
}
random_shuffle(data, data+10);
for( int i = 0; i < 10; i++)
{
cout << data[i] << " ";
}
cout << endl;
SortData(data, 10);
for( int i = 0; i < 10; i++)
{
cout << data[i] << " ";
}
cout << endl;
return 0;
}
2. 一串N个元素(不一定是整数),若存在某一个元素出现次数在一半以上,则成为“众数”,现在给你一串N个元素,问怎么快速并且节省时间地判断众数是否存在,如果存在找出这个元素。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
bool HasMorehalfNum( int data[], int n, int &num)
{
int count = 0, cur = 0;
bool isNew = false;
for( int i = 0; i < n; i++)
{
isNew = false;
if(count == 0)
{
cur = data[i];
count = 1;
isNew = true;
}
else if(data[i] == cur)
{
count ++;
}
else if(data[i] != cur)
{
count --;
}
}
if(cout >= 0 && !isNew)
{
num = cur;
return true;
}
return false;
}
int main()
{
int data[] = {2, 3, 2, 2, 5, 4, 2, 2, 1, 2};
int num = -1;
if(HasMorehalfNum( data, 10, num))
{
cout << "The Number is: " << num << endl;
}
else
{
cout << "The Number is not exist!" << endl;
}
return 0;
} 3. 给定两个整数数组a[],b[]和一个公式a^6-a^2*b^2-b^4 = 2009(注意,是a的6次方,a的2次方),要求设计一个算法快速
地找出合适的a和b。
可以先对数组b 进行排序,排序完成之后,遍历数组a[]中元素,使用二分搜索的方法对数组b[]中的元素进行查找
找到合适的元素。
4. 给定两个已经排好序的实数数组a[]和b[],如果对两个数字组合并排序会形成一个新的数组,这个数组会有一个中位数(排在数组中间的那个数),要求使用a[]和b[]找到那个中位数。(答案转自: http://blog.csdn.net/zcsylj/article/details/6802062)
第一题:假设两个有序数组(已经各自排序完成了)长度相等,试写函数找出两个数组合并后的中位数。
解析: 这个题目看起来非常简单。第一题的话: 假设数组长度为n, 那么我就把数组1和数组2直接合并,然后再直接找到中间元素。对于这样的方案,第一题和第一题就没有什么区别了。这样的话时间复杂度就是O(n)。通常在这样的情况下,那些mentor类型的达人就会循循善诱道:“你还有更好的办法吗:)” 如果比线性更高效,直接能想到的就是对数了O(log(n)),这个时间复杂度在这里可能吗?当然还是可能的。来继续看看下面的分析。先找来了一个图(自己画的,简陋了点)

我们先来分析看看:想到对数的效率,首先想到的就是二分查找,对于这个题目二分查找的意义在哪里呢?
我们找到了A[n/2]和B[n/2]来比较,
如果他们相等,那样的话,我们的搜索结束了,因为答案已经找到了A[n/2]就肯定是排序后的中位数了。
如果我们发现 B[n/2]>A[n/2],说明什么,这个数字应该在 A[n/2]->A[n]这个序列里面,或者在 B[1]-B[n/4]这里面。或者,这里的或者是很重要的,我们可以说,我们已经成功的把问题变成了在排序完成的数组A[n/2]-A[n]和B[0]-B[n/2]里面找到合并以后的中位数,显然递归是个不错的选择了。
类似的,如果B[n/2]<A[n/2]呢?显然就是在A[0]-A[n/2]和B[n/2]-B[n]里面寻找了。
再继续想,这个递归什么时候收敛呢?当然一个case就是相等的值出现, 如果不出现等到这个n==1的时候也就结束了。照着这样的思路,我们比较容易写出如下的代码,当然边界的值需要自己思量一下,前面的想法只是想法而已。
int find_median_equal_length( int a[], int b[], int length)
{
if (length == 1)
return a[0];
int i = length / 2;
if (a[i] == b[i])
return a[i];
else if (a[i] < b[i])
return find_median_equal_length( &a[i], &b[0], length-i);
else
return find_median_equal_length( &a[0], &b[i], length-i);
}
马上有人说那不定长的怎么办呢?一样的,我们还是来画个图看看:(我的画图水平肯定提高了)
第二题:假设两个有序数组长度不等,一样的求出中位数
一样的,我们还是把这个两个数组来比较一下,不失一般性,我们假定B数组比A数组长一点。A的长度为n, B的长度为m。比较A[n/2]和B[m/2]时候。类似的,我们还是分成几种情况来讨论:a.如果A[n/2] == B[m/2],那么很显然,我们的讨论结束了。A[n/2]就已经是中位数,这个和他们各自的长度是奇数或者偶数无关。
b.如果A[n/2] < B[m/2],那么,我们可以知道这个中位数肯定不在[A[0],A[n/2])这个区间内,同时也不在[B[m/2],B[m]]这个区间里面。这个时候,我们不能冲动地把[A[0],A[n/2])和[B[m/2],B[m]]全部扔掉。我们只需要把[B[m-n/2],B[m]]和[A[0],A[n/2])扔掉就可以了。(如图所示的红色线框),这样我们就把我们的问题成功转换成了如何在A[n/2]->A[n]这个长度为n/2的数组和B[1]-B[m-n/2]这个长度为m-n/2的数组里面找中位数了。问题复杂度即可下降了。
c.只剩下A[n/2] > B[m/2],和b类似的,我们可以把A[n/2]->A[n]这块以及B[1]->B[n/2]这块扔掉了就行,然后继续递归。
我们也可以写下如下的代码:
int find_median_random_length( int a[], int lengtha, int b[], int lengthb)
{
int ma = lengtha/2;
int nb = lengthb/2;
int l = ma <= nb ? ma: nb;
if (lengtha == 1)
{
if (lengthb%2==0)
{
if (a[0] >= b[nb])
return b[nb];
else if (a[0] <= b[nb-1])
return b[nb-1];
return a[0];
}
else
return b[nb];
}
else if (lengthb == 1)
{
if (lengtha%2==0)
{
if (b[0] >= a[ma])
return a[ma];
else if (b[0]<=a[ma-1])
return a[ma-1];
return b[0];
}
else
return a[ma];
}
if ( a[ma] == b[nb] )
return a[ma];
else if ( a[ma] < b[nb] )
return find_median_random_length(&a[ma],lengtha-l,&b[0],lengthb-l);
else
return find_median_random_length(&a[0],lengtha-l,&b[nb],lengthb-l);
}
在一些特定的case下面测试了一下,结果还是正确的,下面是用的testcase
int _tmain(int argc, _TCHAR* argv[])
{
int a[] = {1,2,3,6,8} ;
int b[] = {6,7,8,9,10};
std::cout<<"median for equal length is : "<<find_median_equal_length(a, b, sizeof(a)/sizeof(a[0]))<<std::endl; ;
int c[] = {1,3,5,7,9,11} ;
int d[] = {2,4,6,8,10,12};
std::cout<<"median for equal length is : "<<find_median_equal_length(c, d, sizeof(c)/sizeof(c[0]))<<std::endl;;
int A[]={1,3,5,7,8,9,10};
int B[]={2,4,6,10,11,12,13,14,17,19,20};
int sizeA = sizeof(A)/sizeof(int);
int sizeB = sizeof(B)/sizeof(int);
std::cout<<"median : "<<find_median_random_length(A,sizeA,B,sizeB)<<std::endl;;
int C[] = {1, 2, 3, 4, 5, 6, 7};
int D[] = {5, 6, 7, 8, 9};
std::cout<<"median : "<<find_median_random_length(C,sizeof(C)/sizeof(C[0]),D,sizeof(D)/sizeof(D[0]))<<std::endl;;
system("pause");
return 0;
}
5. 36匹马,6个跑道,求最少跑几次可以得到前三名,跑的时候不能记录具体的时间,只能记录相对顺序。
1-1 1-2 1-3 1-4 1-5 1-6
2-1 2-2 2-3 2-4 2-5 2-6
3-1 3-2 3-3 3-4 3-5 3-6
4-1 4-2 4-3 4-4 4-5 4-6
5-1 5-2 5-3 5-4 5-5 5-6
6-1 6-2 6-3 6-4 6-5 6-6
由此,由上图我们可以预见,第一轮中36匹马分为6组,每一组6匹马,然后每一组跑一次。各组得出名次。
第二轮取出每一组的第一名,跑一场,得到一个排名,然后取出前三名。将前三名对应的组的马挑选出来三匹再赛,挑选规则:
第一名对应的一组中,挑选出第一轮比赛中的二三名,第二名对应的组中,挑选第一轮比赛中的第二名,这样就有六匹马再赛依次,即可的得出前3名。
6. 有100层楼的一个楼房,另外有一种特殊的玻璃杯子,可以站在任何一层的阳台上往地面扔杯子,现在可以确定从某一层把杯子扔下去就会碎,低于这层的地方扔下去肯定不会碎,但是没有人知道这个层数确切是多少,有人说是5,有人说是50,就像一个传输。现在只给你两个杯子,需要确定那个杯子扔下去会碎的临界层数是多少,问,让你使用一种选择层数的策略使得最坏情况下确定那个临界层数需要扔杯子的次数最小,注意没有摔坏的杯子可以再扔。
答案转自:http://blog.csdn.net/taylor_tao/article/details/7084467
下图中所有图示的红线均表示剩下两个杯子的时候的试摔位置,当杯子破碎后,也就是只剩下一个杯子的时候,只需要从已知范围的最底层向已知范围的最高层逐层试摔。
当有一层的时候,需要一次试摔。
当有两层的时候,需要两次试摔。
当需要三层时候,首先讨论是否可以通过两次试摔完成,可以发现可以,方法如图。
当需要四层时候,首先讨论是否可以通过两次试摔完成,可以发现已经不行,因此至少需要三次试摔。
当需要五层时候,首先讨论是否可以通过小于等于三次试摔完成,如果不行则讨论最多四次试摔的情况。依次类推,如下图:

因此,当有100层的时候,最多需要n次试摔,使得 n+(n-1)+(n-2)+...+1 >= 100,然后对n上取整,因此n=14。最差情况需要14次试摔。试摔方法为:第一次在14层扔,如果没破,在27层(14+13)继续扔,不破在39层(27+12)继续扔,依次类推。如果破了,剩下一个杯子,从已知范围的最底层向已知范围的最高层逐层试摔。
7. 写快速排序算法
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int mypartition( int data[], int start, int end)
{
int pivot = data[end];
int k = start - 1;
for( int i = start; i < end; i++)
{
if(data[i] < pivot)
{
++k;
int tmp = data[k];
data[k] = data[i];
data[i] = tmp;
}
}
++k;
int tmp = data[k];
data[k] = data[end];
data[end] = tmp;
return k;
}
void quicksort( int data[], int start, int end)
{
if( start < end)
{
int pivot = mypartition( data, start, end);
quicksort( data, start, pivot-1);
quicksort( data, pivot+1, end);
}
}
int main()
{
int data[] = {2, 3, 2, 2, 5, 4, 2, 2, 1, 2};
for( int i = 0; i < 10; i++)
{
cout << data[i] << " ";
}
cout << endl;
quicksort(data, 0, 9);
for( int i = 0; i < 10; i++)
{
cout << data[i] << " ";
}
cout << endl;
return 0;
} 8. 有一个岔道口两条路,一条通往A(那里的人只讲真话),另外一条通往B(那里的人只说谎),这事两条路上各走过来一个人都是当地人,且知道对方的来历,你只能问他们其中的一个人一个问题,对方只会回答"是"或“不是”,怎么才能知道那条路通往A
问其中一个人一个常识性的问题,例如你是男的吗?从而确定另外一个人是说谎还是说真话,即可得到通往A的路
9. 输入n,生成(2n+1)阶矩阵;例如,输入1 生成
7 8 9
6 1 2
5 4 3 。即生成螺旋矩阵的程序。
#include <iostream>
#include <vector>
#include <algorithm>
#include <fstream>
using namespace std;
#define N 10
int ar[N][N];
void SpiralArray(int size)
{
int a = size*2+1; //保证边长为奇数
int y = a / 2,x = a / 2; //从中心点开始
for ( int i = 1; i <= a*a; i++)
{
if ( x <= a-y-1 && x >= y) //
{
ar[y][x]=i;
x++;
}
else if (x>a-y-1&&x>y)
{
ar[y][x]=i;
y++;
}
else if (x>a-y-1&&x<=y)
{
ar[y][x]=i;
x--;
}
else if (x<=a-y-1&&x<y)
{
ar[y][x]=i;
y--;
}
}
}
int main()
{
SpiralArray(1);
for(int i = 0; i < 2*1+1; i++)
{
for(int j = 0; j < 2*1+1; j++)
{
cout << ar[i][j] << " ";
}
cout << endl;
}
cout << endl;
return 0;
}
By Andy @ 2013年10月21日