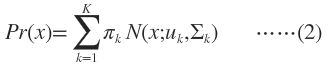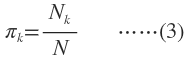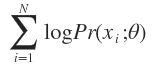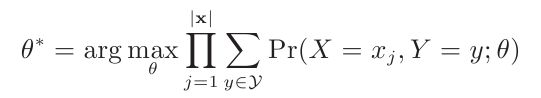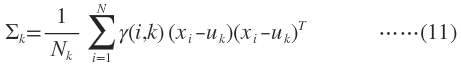EM及高斯混合模型

本文就高斯混合模型（GMM,Gaussian Mixture Model）参数如何确立这个问题，详细讲解期望最大化（EM,Expectation Maximization）算法的实施过程。

单高斯分布模型GSM

多维变量X服从高斯分布时，它的概率密度函数PDF为：

x是维度为d的列向量，u是模型期望，Σ是模型方差。在实际应用中u通常用样本均值来代替，Σ通常用样本方差来代替。很容易判断一个样x本是否属于类别C。因为每个类别都有自己的u和Σ，把x代入（1）式，当概率大于一定阈值时我们就认为x属于C类。

从几何上讲，单高斯分布模型在二维空间应该近似于椭圆，在三维空间上近似于椭球。遗憾的是在很多分类问题中，属于同一类别的样本点并不满足“椭圆”分布的特性。这就引入了高斯混合模型。

高斯混合模型GMM

GMM认为数据是从几个GSM中生成出来的，即

K需要事先确定好，就像K-means中的K一样。 πk 是权值因子。其中的任意一个高斯分布N(x;u_k,Σ_k)叫作这个模型的一个component。这里有个问题，为什么我们要假设数据是由若干个高斯分布组合而成的，而不假设是其他分布呢？实际上不管是什么分布，只K取得足够大，这个XX Mixture Model就会变得足够复杂，就可以用来逼近任意连续的概率密度分布。只是因为高斯函数具有良好的计算性能，所GMM被广泛地应用。

GMM是一种聚类算法，每个component就是一个聚类中心。即在只有样本点，不知道样本分类（含有隐含变量）的情况下，计算出模型参数（π，u和Σ）----这显然可以用EM算法来求解。再用训练好的模型去差别样本所属的分类，方法是：step1随机选择K个component中的一个（被选中的概率是 πk ）；step2把样本代入刚选好的component，判断是否属于这个类别，如果不属于则回到step1。

样本分类已知情况下的GMM

当每个样本所属分类已知时，GMM的参数非常好确定，直接利用Maximum Likelihood。设样本容量为N，属于K个分类的样本数量分别是N₁,N₂,...,N_k，属于第k个分类的样本集合是L(k)。

样本分类未知情况下的GMM

有N个数据点，服从某种分布Pr(x;θ)，我们想找到一组参数θ，使得生成这些数据点的概率最大，这个概率就是

称为似然函数（Lilelihood Function）。通常单个点的概率很小，连乘之后数据会更小，容易造成浮点数下溢，所以一般取其对数，变成

称为log-likelihood function。

GMM的log-likelihood function就是：

这里每个样本x_i所属的类别z_k是不知道的。Z是隐含变量。

我们就是要找到最佳的模型参数，使得(6)式所示的期望最大，“期望最大化算法”名字由此而来。

EM法求解

EM要求解的问题一般形式是

Y是隐含变量。

我们已经知道如果数据点的分类标签Y是已知的，那么求解模型参数直接利用Maximum Likelihood就可以了。EM算法的基本思路是：随机初始化一组参数θ⁽⁰⁾，根据后验概率Pr(Y|X;θ)来更新Y的期望E(Y)，然后用E(Y)代替Y求出新的模型参数θ⁽¹⁾。如此迭代直到θ趋于稳定。

E-Step E就是Expectation的意思，就是假设模型参数已知的情况下求隐含变量Z分别取z₁,z₂,...的期望，亦即Z分别取z₁,z₂,...的概率。在GMM中就是求数据点由各个 component生成的概率。

注意到我们在Z的后验概率前面乘以了一个权值因子α_k，它表示在训练集中数据点属于类别z_k的频率，在GMM中它就是π_k。

 M-Step M就是Maximization的意思，就是用最大似然的方法求出模型参数。现在我们认为上一步求出的r(i,k)就是“数据点x_i由component k生成的概率”。根据公式(3),(4),(5)可以推出：

与K-means比较

相同点：都是可用于聚类的算法；都需要指定K值。

不同点：GMM可以给出一个样本属于某类的概率是多少。