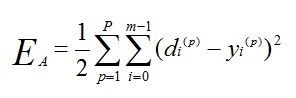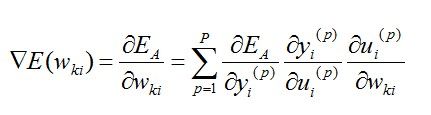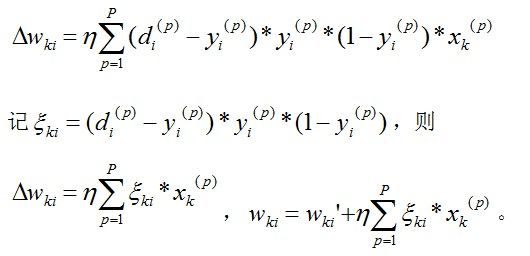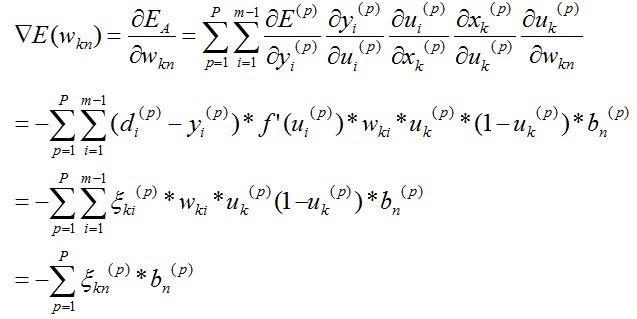BP神经网络算法推导

一：算法推导

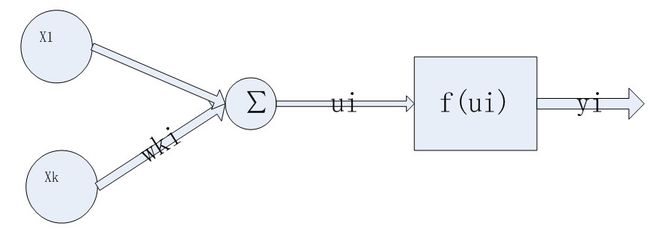
　　神经网络通过模拟人的神经元活动，来构造分类器。它的基本组成单元称为”神经元”，离线情况下如果输入大于某值时，设定神经元处于兴奋状态，产生输出，否则不响应。而这个输入来自于所有其它的神经元。而神经元的响应函数有多种(需要满足可微，这种简单的函数可以拟合任何非线性函数)，本文选择sigmod函数。关于基础知识在此不在多说，这里主要介绍一下BP神经网络，并推导权值和阈值的更新公式。

 

　　BP网络通过前向反馈误差来改变权值和阈值，当网络的输出与实际期望的输出均方误差低于某个阈值或者学习次数满足一定条件时，训练完成。首先给出输出均方误差的公式：

 

 

　　其中，m是输出节点个数，p是训练样本个数。我们就是以最小化这个EA为目标更新网络参数。这里以3层网络为例进行推导，即一个输入层、隐含层、输出层。最小化目标函数采用梯度下降的方法。

1、隐含层到输出层的权值更新

　　K为隐含层节点数，i为输出节点个数。权值更新公式：

 

其中wki表示第k个隐含节点到第i个输出节点之间的权重，η为学习率，是一个使得求解快速收敛的学习因子，为EA关于wki的梯度。即：

因为：

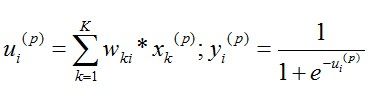，其中，激活函数对x求导后，y'=y(1-y),所以进一步求得：

这就是wki的梯度值。记:

，表示为权值的增量，则权值更新可写成：

其中增量:

所以根据这个式子我们就可以更新权值了。

 

2.输入层到隐含层的权值更新

 

　　同理，误差关于权值的梯度可通过以下式子求解，与上面有点不同的是：输入层与隐含节点之间的权值将影响所有的隐含节点到输出层之间的值，所以此时的权值梯度信息应该对误差在隐含层与输出层之间产生累加效应。废话不多说，直接上图上公式更明了：

其中，

所以这一层的权值增量也可以写成这样的形式：

参考：

 

http://www.cnblogs.com/hellope/archive/2012/07/05/2577814.html

http://baike.baidu.com/view/1753676.htm