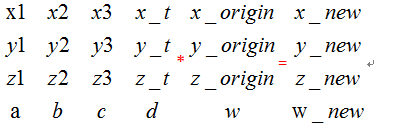3D坐标系、矩阵变换、视景体与裁剪
背景
当前3D图形界主要有两个：微软的Direct 3D以及某组织的OpenGL。曾经一度OpenGL几乎占据所有3D图形领域，这在巨人微软面前简直就是屌丝逆袭。曾几何时微软搞IDE borland公式倒闭了，后来微软搞浏览器，网景公司解散，员工卷铺盖走人了，也就是说微软搞谁，谁倒霉。直到OpenGL的出现，打破了这一魔咒，在与微软竞争的前期，OpenGL几乎甩了微软几条街，并成为事实上的工业标准。后来在微软的大力绞杀下，OpenGL几乎被完全赶出了游戏领域，退居高端图形领域。基本上现在是微软的Direct 3D统治游戏领域，而OpenGL则在高端专业图形领域占绝对统治地位。微软还是微软，OpenGL已经不是以前的OpenGL了，等会。。等会。。这句话咋这么熟悉？想起来了赵本山的小品里说过：你大爷还是你大爷，你大妈已经不是你5年前的大妈了，为什么这么说呢？话说搞OpenGL的那家公司被微软逼疯了，没错。。解散了。。但是OpenGL并没有消失，而是交给某开源组织托管、开发与维护了。哎。。。不说了，都是泪啊。。凡是牵扯到微软，那就是一部血泪史啊。。逼疯了无数企业。。但是话有说回来，商场上比尔盖茨是个侩子手而慈善上这家伙也不小气。。大把大把的捐钱。。
坐标系空间
在OpenGL里面，3D坐标系的X轴自左向右增大，y轴自下向上增大，z轴正方向从屏幕中心指向观察者。
坐标系有以下几种：局部(模型)坐标系、世界坐标系、相机坐标系、屏幕坐标系；对应的矩阵变换则有模型变换、视图(相机)变换、投影变换，其中投影变换分为正视投影、透视投影。而坐标系之间的转换要用到矩阵。世界坐标系相当于是虚拟宇宙，位置固定不变，而局部(模型)坐标系是绘图的一个局部空间，是相对的，相机坐标系是以相机的镜头(或者人的眼睛)来观察物体的视觉空间。在3D中画图是现在局部坐标空间绘制，然后通过矩阵变换转移到世界坐标空间，接着转换到相机空间，然后在投影，最终会在光栅化的二维屏幕上渲染图形。
局部坐标空间又叫模型空间，绘制图形是在模型空间绘制，绘制完成后经过模型变换转换到世界坐标系空间。在OpenGL中渲染三维模型是以图元为最小单位进行渲染的，图元有三角形，四边形等，绝大多数情况下都是以三角形图元渲染。图元如三角形是有3个顶点组成的，那么为什么最小图元不是顶点而是诸如三角形呢？这就好比提到一个化学物质人们会说这个物质是由很多原子组成的，而不会说是由电子、中子、原子核组成，因为电子、中子及原子核是一个有机整体；同样三角形图形的三个顶点也是一个有机整体。
图一
图二
上面图片一是层次细节LOD地形网格，513像素X513像素，不过并没有达到完全的分辨率，而且不同的地方分辨率不同，此是后话。图片二是用OpenGL加载的一个ms3d格式的三维小汽车，这个小汽车是用3d max制作的3ds文件经过MilkShape 3D转换后得到的ms3d文件。这两个三维模型都是以三角形网格渲染而成的，不同的是图一没有进行文理贴图，而是以线框的模式渲染的，这样做是为了更好的看到3D渲染的细节；对应的图二则是以平滑模式渲染并且贴有文理。从本质上来说三维图像的最小单位是顶点，这些顶点以特定的方式送往3D API(典型的如OpenGL 3d api或者D3D api)并以三角形网格的形式进行渲染。当然也可以选择其他多边形如四边形进行渲染，但是三角形渲染最为方便，几乎所有的3D图形都是以三角形为图元进行渲染。从图一可以看出这个地形是有很多小的三角形网格组成的，事实上这个地形网格是以三角形扇的方式组织渲染的。现在我们看到的这两个图形是在屏幕坐标空间观察的，那么他们的第一站其实就是局部(模型)坐标空间，经过一系列3D流水线最终送往二维屏幕进行光栅化处理和渲染。在局部坐标系的物体有N个顶点组成，如果变换到世界坐标系的话需要对所有顶点做变换，共计N次变换。设物体的任一顶点为(loc_x ,loc_y , loc_z)。这个坐标是在局部坐标系下，要想变换到世界坐标空间需要将局部坐标系的原点移动到对应的位置(world_x,world_y,world_z)处，并且同时移动三维模型的所有顶点坐标。很容易得到最终的坐标：(loc_x+world_x,loc_y+world_y,loc_z+world_z)。现在我们先来看一幅图片：
我们惊奇的发现这个计算结果正是我们想要的，没错，你猜对了，在3D图形里面顶点的变换都是通过矩阵完成的，而这个平移变换是最简单的一种矩阵变换，其他的还有旋转、缩放等等。上面的图一、二就是在3D流水线里经过一些列像上述那样的矩阵变换最终才从幕后走向台前展现在大家眼前。由上可以看出每一个顶点经历了16次乘法运算、12次加法运算，共计28N次计算，当然在矩阵变换之间可能还有进行了诸如光照、纹理等操作。假如一个三维场景共有100万个顶点，那么就要做2800万次计算，这还没有加上后面的相机变换、投影变换所做的矩阵运算以及光栅化、渲染等操作。由此可以看出来运算量是非常的大。那么显卡能承受如此巨大的运算量吗？后面会提到，3D 图形库(如OpenGL)会在图形进行渲染前将不必要的顶点裁剪掉，这样就不用渲染他们了，从而节省了GPU的运算量。但是光是依靠3D 图形库的裁剪功能还是不够，虽然裁剪掉了不需进行渲染的顶点，然而这些顶点已经消耗掉了大量的矩阵运算，尤其是当场景非常细腻的时候也就意味着顶点数目非常巨大。那么有没有方法可以在坐标系统进行矩阵变换前就被提前裁剪掉呢？答案是肯定的。举个例子，对于图一中的地形网格来说，他被渲染到屏幕是有条件的，其一：不在照相机视景体空间内的物体将被忽略不予处理；其二：对于远处的地面以低分辨率渲染，近处则以高分辨率渲染；其三：粗糙的部分以高分辨率渲染，平坦的部分以低分辨率渲染。假如有一个600X600的网格经过测试不在照相机的视景体内，那么这36万个顶点就不用进行后续的大量矩阵运算，而测试所消耗是由8个顶点组成的六面体，这个运算量的消耗无疑是值得的。至于如何进行相机裁剪，在层次细节算法里面将会详细说明。在OpenGL以及D3D里面用户一般不会直接操作矩阵，OpenGL会将用户的函数调用解释为矩阵，比如用户调用gluPerspective(参数。。)时，OpenGL会根据函数的参数设置视图矩阵并与当前的视图矩阵相乘。
世界坐标系空间经过上面的平移操作物体就被移动到世界坐标系，这个坐标系是固定不变的，相当于虚拟宇宙中心。此时物体还不能呈现于屏幕，还要经历九九八十一难才能与观众见面。进入世界坐标系以后，照相机的视点可能不在原点，并且视点可能还不是朝向z轴负方向。此时就要将照相机平移到世界坐标系原点，并且调整方向使相机视点朝向z轴负方向。之所以要这样调整是因为如果相机位于原点并朝向z轴负方向的话会给处理带来极大的方便，至于是什么方便呢，我也不知道，反正是专家说的，至于你信不信，反正我是信了。在说明如何变换到相机空间我们先来看一下几个矩阵操作。设有世界坐标系空间的某一个点A(world_x,world_y,world_z)分别绕x轴 y轴 z轴旋转angle_x、angle_y、angle_z度到达B点。那么求其旋转后的坐标。
图三
这里为了更好推导将坐标系进行了旋转。
如图三A点绕x轴 旋转angle_x度求其旋转后的坐标。A点绕X轴旋转所形成的平面必定与y轴 z轴所构成的平面平行，因此将A点 B点投射到y_z平面上得到A撇点 B撇点，A撇 B撇点在z y平面上的坐标显而易见就是A点 B点对应的 y z坐标。如图可知C角的大小就是angle_x 即C=angle_x;D点对应的那个角是OA与y轴的夹角。
对于B撇点:
对于A撇点：
将第一个方程式展开得到:
将第二个方程代入第三个方程式得到：
(world_x, world_y*cos(angle_x)+world_z*sin(angle_x),-world_y*sin(angle_x)+world_z*cos(angle_x));
下面我们再看一个矩阵运算：
矩阵一
我们再一次吃惊的发现这个正是我们所想要的结果，难道冥冥之中矩阵与3D图形变换有着不解之缘？OpenGL里面矩阵是按照列优先的原则存储于一个一维数组里面，三维顶点不是以三维向量二是以四维向量来表示比如(x,y,z,w)来表示的，w初始默认情况下为1，在变换过程中w的值会跟着发生变化，并且w也有它的用处，此是后话。我们来看一个更加一般的矩阵：
在上述的矩阵变换中我们曾经说过绕X轴旋转物体angle_x度，这相当于物体不动把坐标轴绕X轴向相反的方向旋转angle_x度。如图A表示绕X轴旋转的角度，如果以上述变换为例，那么A=angle_x。显然在新的局部坐标系下对应的B C点在原来的坐标系中的坐标分别是
(0,-1*sin(angle_x),1*cos(angle_x)) (0,1*cos(angle_x),1*sin(angle_x)) 再看矩阵一，发现这个正是新的坐标系的三个方向向量，这个方向向量是以原坐标系为参考系得来的。在3D中我们旋转物体与物体不动旋转坐标系的效果是一样的，只是四维方式的问题而已。在回过头来看矩阵二，我们发现(translate_x ,translate_y,translate_z)是局部矩阵的原点在原坐标系下的坐标，而(x1,y1,z1)是新的局部坐标系的x轴上的一个点在原坐标系下的坐标，其他的以此类推，局部坐标系的原点定了，三个坐标轴上的点也定了，我们吃惊的发现局部坐标系在原坐标系为参考的情况下已经描绘出来了。如果。。如果原坐标系是世界坐标系，没错，如果成真的话我们就经过一系列矩阵变换得到了局部坐标系在世界坐标系中的位置，于是就刻画出来了三维物体的顶点坐标在世界坐标系下的坐标值。
现在还记得我们一开始的问题吗？你可能已经不记得了，问题是如何将世界坐标系变换到相机坐标系。
图片来自3D游戏编程大师。
如上图相机位置(cam_x,cam_y,cam_z)与y轴夹角为angle_y。如果要变换到相机空间的话首先要将相机平移到原点，结合前面所说的也就是设置矩阵的最后一列translate_x=-cam_x, translate_y=-cam_y, translate_z=-cam_z，然后使相机的镜头绕y轴旋转-angle_y度。前面已经讲过绕X轴旋转angle_x度的矩阵方程，那么绕x轴旋转-angle_x度的方法就是将前述矩阵的角度设置为-angle_x就行了，y轴旋转的也可以以此类推。
相机坐标空间经过上述的矩阵变换已经到达了相机坐标空间，现在到了投影的时刻了，前面定义了相机的位置和方向，但是相机的视野不是无限远的，必须为它制定一个视景体，在视景体内的物体将被投影到视平面，不在视景体内的物体将被丢弃不处理
如图便是一个视景体，这个投影是透视投影，所谓透视投影就是给人一中置身于实际场景中的感觉，远处的物体显得小，近处的物体显得大。还有一中投影叫正视投影，这个主要用于CAD程序中。三维图形主要使用透视投影。在OpenGL这个视景体可以用api函数gluPerspective(angle,fov,w_div_h,near,far)来定义。这个函数将产生一个透视投影矩阵并与当前的投影矩阵相乘。
投影空间经过上述矩阵变换就到了投影空间了，接着就是后续的视口变换，渲染等工作了。
裁剪现在我们再来看一个地形网格
图片三
这个地形网格和图片一是一个程序生成的，不同的是前者调节系数是8，后者调节系数是25结果导致了后者的分辨率明显大于前者。经过前面坐标系空间变换的介绍我们知道这幅地形网格呈现在我们眼前之前经历了模型变换，视图变换，投影变换等。这个地形网格是513*513尺寸，而且没有达到完全分辨率，那么如果达到了完全分辨率，势必顶点数目大幅增加，再如 如果地形尺寸是10000*10000呢，顶点数将增加400倍，再如一个实际的场景可能还有大量的树木，房屋，动物，人车等。除了矩阵运算还有纹理贴图，光照，雾化等，处理起来相当的消耗GPU和CPU。如果不控制好的话，系统渲染后运行非常卡。其中有一个可以改善的方法是LOD算法即层次细节算法，这个算法常用来绘制大规模实时地形。这个算法其中需要用到一个叫相机裁剪的算法。接下来就说一下相机裁剪。所谓相机裁剪就是在上图视景体中的物体进行处理，不在里面的物体被丢弃。前面已经说过渲染的时候OpenGL会自动丢弃不在视景体内的物体以避免渲染，而此处的裁剪进一步减少了矩阵运算的次数，也就是说如果物体需要裁剪的话，那么在模型空间就被裁剪了，而没有经过后续的各种矩阵变换。那么必须设计一个算法来检测某个物体是否被相机裁剪。方法之一是将待处理的物体构造一个AABB包围盒，然后用包围盒的顶点与物体顶点所在的平面做相交测试，不想交就被裁剪掉，否则保留。
typedef struc aabb
{
someType min[3];
someType max[3];
} AABB;
这个结构体里面min[3]里面保存的是(min_x,min_y,min_z)对应max[3]里面保存(max_x,max_y,max_z) 这些坐标是采用某种方法找到的物体的最小坐标或最大坐标值，最笨最耗时的办法就是遍历物体的每个顶点找到对应的最小最大坐标值
那么怎么求视景体的六个面的方程呢？在OpenGL中经过透视投影后前文的视景体变为了规则的长方体，这个投影空间中顶点的坐标形式为(pro_x,pro_y,pro_z,w)，现在到了w值大显神通的时候了，如果程序员没有在程序中故意操作矩阵的值，那么现在这个w就是每个坐标值得各个分量的绝对值的最大范围，显而易见如果物体的坐标满足-w<x<w;-w<y<w;-w<z<w的话那么物体在这个投影空间内否则被裁减掉。这个投影空间的左平面的方程为x=-w,但是我们把它写作-x-w=0的形式，这样他的法向量就是(-1,0,0)也就是指向投影空间的外部，保证其他六个面的法向量也指向物体外部，这样是为了方便后面的相交测试，当然使所有平面方程的法向量指向空间内部也是可以的，总之保持一致性就可以了。对于一个普通的平面方程A*x+B*y+C*z+D=0和一个顶点(a,b,c)将其代入原方程，如果A*a+B*b+C*c+D=0的话这个顶点就在平面上，若小于零则在平面一侧若大于零则在另一侧，这个方法就可以用于包围盒与相机裁剪测试中。我们的目的是在物体经不经过模型、视图、投影变换直接进行相交测试，那么必然要求得相机视景体在经过相机变换 模型变换前的六面体的6个平面方程。那么从当前的这个投影后的长方体就可以推导出这个所需要的六面体的六个面的方程。设局部坐标系下物体的任意一个顶点是vertex_local=(local_x,local_y,local_z,w)这里w=1;经过投影变换后的坐标vertex_per=(per_x,per_y,per_z);设M是模型变换矩阵，V是相机变换矩阵，P是透视投影变换矩阵。那么将会有如下的坐标变换关系vertex_local*MVP=vertex_per；其中MVP是模型视图投影三个矩阵的乘积，这个是显而易见的。这是目前可以利用的一个等式，我们就是从这个等式推导出面的方程。这其中的矩阵M V P分别是模型 视图 投影矩阵，可以由OpenGL api获得，然后计算其乘积就行了。先来看一个图片：
在这个矩阵乘法当中一个原始坐标乘以一个4*4矩阵得到一个新的坐标。
其中 x_new=X1*x_origin+x2*y_origin+x3*z_origin+x_t*w;
w_new= a*x_origin+b*y_origin+c*z_origin+d*w;
由上述可知投影之后在x轴方向的范围是[-w_new,w_new]
所以右平面上的点的方程式x_new=w_new;
结合上两个方程式得到：x_origin*(X1-a)+y_origin*(X2-b) +z_origin*(X3-c)+w*(x_t-d)=0;
由于初始w=1;所以 x_origin*(X1-a)+y_origin*(X2-b) +z_origin*(X3-c)+(x_t-d)=0;
其中小括号里的数据是可以计算出来的，相当于常量，于是上式的形式就是Ax+By+Cz+D=0。显然这是个平面的方程，而x y z是初始的点，那么这个方程就是初始的点所在的平面的方程。同样道理求得另外5个面的方程，然后做相交测试，便可以进行裁剪了。现在包围盒aabb 六个平面的方程已经了。
那么现在如何进行相交测试呢？
如图一开始最小 最大点是红色的min max点，经过轴分离后最小 最大点变化为绿色的min max在知道包围盒aabb和6个平面的方程后就可以使用轴分离方向来测试相交问题。如果aabb最小的点在某个平面外的话，那么其他点一定在平面外。但是现在有一个问题就是怎么定义最大最小点，最大最小分别表示距离平面距离最大最小的点。一开始没有考虑平面的时候直接比较坐标值的大小来确定最大最小点，现在引入平面方程后就要重新调整aabb得到新的包围盒。这里不试图给出严格的数学证明，只举一个简单的例子来说明为何要重新调整aabb。轴分离的话就是分别考虑x y z轴。现在假设考虑x轴，上述的投影后的长方体左平面方程为-x-w=0；假设aabb.max[]={-3,-3,-3} aabb.min[]={-5,-5,-5}但是现在距离-x-w=0(w<1.0) 最小的点显然是{-3,-5,-5) 最大点显然应该是(-5,-3,-3)，然后y z轴以此类推，得到更新后的aabb。将新的aabb.min代入上面的平面方程如果大于0的话，算法立刻return，这个aabb不在视镜体内，如果小于0的话，在将aabb.max代入，如果大于0的话设置标志insect=true;然后循环处理另外几个平面方程。最终若aabb不在包围盒内将会在循环的过程中return，如果循环顺利结束，并且insect=true,说明aabb与视景体相交，否则aabb完全在视景体中。
自此，本文就结束了，这只是任务中的一个小部分。。还有很多其他任务需要做。。