dlmalloc 2.8.6 源码详解(5)

本文章由vector03原创, 转载请注明出处.

邮箱地址: [email protected], 欢迎来信讨论.

 

 

3. 分配及实现

本章节介绍dlmalloc的分配算法和实现.由于存在多mspace的情况, dlmalloc使用了两套API.一套对应默认的mspace,以dl前缀开头,如dlmalloc, dlrealloc等.如果创建了自定义的mspace,则使用mspace开头的API,如mspace_malloc, mspace_realloc等.但两套API在基础算法上是一致的.我们就以默认的API为主要对象介绍.

3.1 算法概览

事实上, dlmalloc虽然复杂,核心算法却非常简单,如果有前面章节的基础很容易就能看懂.

核心分配算法针对small request和large request概括起来各五句话(注意这里的分配请求大小都是经过align和padding处理后的大小),对应small request(<256字节),

1.         首先在分配请求对应大小的分箱以及更大一级分箱中查找, 如果有则返回,否则进入下一步.选择这两个分箱因为它们最接近分配目标大小,且剩余部分都无法单独成为一个chunk (原文中称之为remainderless chunk).

2.         如果dv大小足够满足,则切割dv chunk,否则进入下一步.

3.         在所有分箱范围内查找(包括small bins和tree bins),找到可以满足需求的最小的chunk,切割,将剩余部分指定为新的dv,否则进入下一步.

4.         如果top chunk满足需求,则切割top,否则进入下一步.

5.         从系统获取内存并使用它.

对应large request,

1.         从tree bins中查找最小可用的tchunk,如果其比dv更加适合(更接近目标大小),就使用该chunk.如果其剩余部分超过最小可分配chunk,则切割它.否则进入下一步.

2.         如果dv满足需求,且比任何分箱中的chunk更适合,则使用dv,否则进入下一步.

3.         如果top满足需求,则使用top,否则进入下一步.

4.         如果分配请求大于mmap_threshold阈值,则直接通过mmap分配,否则进入下一步.

5.         从系统获取内存并使用它.

从类型上, dlmalloc属于best-fit型分配器,只是Doug Lea在此基础上做了诸多优化.本质上都是本着物尽其用的思想来挑选合适的free chunk, 只有当不能首先满足时, dlmalloc会通过dv和top来做进一步的挑选,这就最大限度的减小了内部碎片产生.同时dv和top的存在也能比较有效的减少外部碎片.

而如果外部请求过大, dlmalloc不是优先获取系统内存后分配,反而倾向于直接通过mmap获取.原因在于位于top的free chunk有可能因为相邻高地址的alloced chunk而一直无法释放.如果dlmalloc向系统申请了大块内存,即便被应用程序free,也可能因为auto trmming失败而导致它们长期驻留在top space中.而直接mmap的好处就是随时可以将这些huge chunk返回给系统,只要应用程序决定不再使用它们.

下面是更详细的代码分析,

基本上还是比较好理解的, 下面对一些地方做展开说明,

1.         Line5491, 这里如果使用lock, 会在开始确认一些全局参数是否初始化.这些参数保存在名为mparams的全局变量里,类型为malloc_params,包含交叉检查的magic,当前系统页面大小,设定的粒度大小, mmap的阈值, trimming阈值以及默认的mspace参数.并且以magic作为参数初始化的标志.

2.         Line4595, PREACTION和POSTACTION成对出现,就是加锁和解锁.因为是平台相关的,针对不同系统需要有具体的实现.从这里其实也可以看出dlmalloc对多线程条件下的分配设计的还是比较简陋的,关注的还是单线程下分配算法的实现.

3.         Line4619, 这里是一个对double link list首节点的删除操作,且如果list为空就更新small map.注意, dlmalloc为了提高list处理速度,是设计了头节点的,因此这个first chunk并不是头节点,而是其前一个节点.这个曾经在前面的章节提到过,可以通过这里的具体实现看到这些优势,其中B指代list头节点, P是需要删除的节点.

 

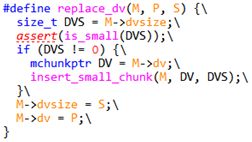
4.         Line4663, 是替换dv的过程,旧dv如果还存在,会送回到分箱系统中管理,而新的chunk作为其替代. M指mstate, P是继任dv, S为继任dv大小.

这里insert_small_chunk是前面删除的反向操作,实现如下,

在插入的同时, 会对small map进行维护操作.

3.2 tmalloc_small

tmalloc_small是在tree bins中分配small chunk的子函数.用于small request的核心分配算法3,即当remainderless和dv都无法满足,且剩余small bins也没有free chunk时,从tree bins中搜索.

代码本身其实比较容易理解, 源码注释如下,

两点说明,

1.         Line4537, 寻找DST最小节点通过宏leftmost_child完成,该宏的定义如下,

这里涉及到最小节点的遍历. 我们知道, 对于BST来说,根节点与左右子树有严格的排序关系,因此查找最小节点就是从根节点出发向左子树步进,一直遇到左子树为null停止的过程.

但如2.2.5小节中所述, DST本就不是一棵排序树,根节点同子树间不能确定大小关系,相比之下获取最小节点就更困难一些.但可以确定的一点是,同一级level中,越靠近左侧的子树节点就越小,因此我们可以大致圈定最小节点出现的范围,如下,

上图中用颜色标记了每一级level最左侧的节点(不限于左子树或右子树),尽管暂时还无法断定哪一个是最小节点,但它肯定出现在从A到E的路径上.所以DST的搜索路径为,从根节点出发,一路向左子树步进,若遇到左子树为空,就转头向右子树,一直遇到左右子树都为空停止.换句话说,沿着整棵DST的最左侧边缘走,如图所示

关于这一点, 我想应该是DST最大的缺陷,因为无论如何,遍历的次数是与树高相关的,上图中最小节点可能出现在位置C,但你需要完成每一次比较才能最后下决定.不过好在对于size_t等于4字节的系统,树高最多也只有32.无论如何这比线性查找还是要快得多了.

2.         Line4551, 与DST的删除操作相关.由于unlink_large_chunk宏的代码比较长,还是先说明一下节点删除算法.基本上, Doug Lea的DST删除算法分为三个步骤,

第一步, 判断待删除节点X是否存在相同大小的兄弟节点.如果有,只要简单的将其从双链表上摘除再重新接好链表即可.如图,

第二步, 如果节点X所在位置只有其一个节点,就需要选出一个继任节点R以替代X空缺的位置,同时还要保证DST的性质.由于DST也属于前缀树(prefix tree)的一种,因此子树节点提升level是很容易的,但降低level情况就相对复杂了.比如,子树节点前缀为0101,可以提升为010,但如果下降为0101x…x就必须参考其他子树的情况.如图,

这里如果我们选择R作为继任节点,则原节点X的左子树节点L就要改变其level.这时必须参考子树R的情况,为L寻找一个合适的插入点.如果R的内部很复杂,这个过程就会相对漫长.

因此Doug Lea取了个巧,他选择了right-most叶子节点作为X的继任节点.既然是叶节点,只需要简单的提升level即可,其他子树节点的level和位置都不会发生任何变化,于是就绕过了上述问题.选择right-most的原因还在于, dlmalloc在遍历best-fit节点时,会按照left-most的路径查找,导致多数情况下,左子树节点数少于右子树.为了平衡左右子树,同时削减子树高度,选择right-most相比更为合适,如图,

上图中查找到子树X的right-most节点R,用其替换X空缺的位置,可以看到L节点等子树节点位置没有任何变化.同时,改变R的位置平衡了左至右子树,让DST整体更均衡.

第三步, 这里就比较清楚了,只需要重新连接继任节点与原X的父节点和左右子树节点即可.

整个过程的源码注释如下,

3.3 tmalloc_large

该函数是在tree bins中分配large request的子函数.与tmalloc_small略有区别, large request并不是寻找最小节点,而是best-fit节点,即一个大于等于期望值的最小节点.

基本算法如下,

1.         以分配请求大小nb作为key值进行基值检索,并做两点记录.一是记录最接近的候选节点v,另一个记录当前最近的未被遍历的右子树节点rst (The deepest untaken right subtree).同时如果找到相同大小的chunk则立即返回.

2.         若已遍历到子树的最下层, 则返回记录的rst子树节点,从这个位置开始进行left-most遍历,这里同tmalloc_small中寻找最小子树节点是一致的.

3.         若找不到可用节点, 则从treemap中寻找最小可用分箱,从可用分箱中寻找.

4.         若dv比候选节点v更适合,则直接返回0,否则切割候选节点,并最终返回payload.

在同一分箱内的搜索过程如图所示,

在一个分箱内, 搜索best-fit节点按照从A到F的顺序执行.其中A-D属于基值检索,以nb的前缀为key值,而E-F则按照left-most检索,因为E子树是当前分箱中大于目标值的最小子树,只要找到最小节点即可.从这里也可以看出这个算法本质上很简单,就是先按照前缀寻找最接近的目标节点,如果没有则扩大范围在大于目标值的最小子树中搜索,还没有再到最接近的更大的分箱中查找,直到找到为止.

代码注释如下,

Line4465, Line4480, Line4490,这三处地方其实就是对nb掩码逐bit位的测试操作,以进行基值检索.

该宏展开如下,

看上去有些复杂, 其实就是除最高有效位以及次最高有效位之外, 将后续bit位移动到msb端.之后每次循环就取出一位进行检测.如下图所示,

稍微不好理解的就是i >> 1的作用.回顾一下2.2.4小节中tree bins索引寻址的说明,这里就是computer_tree_index的逆运算.结果是不算末尾8bit,最高有效位的位号.这里减2的原因是最高有效和次高有效位用于计算分箱号,因此不计入key值.位移后获得的掩码在检测时会重新右移至最低位,并提取以决定是向左子树还是右子树步进.在整个循环中会不断左移掩码以保证遍历持续进行,直至达到最底层子树节点.

事实上这个宏Doug Lea搞得有点麻烦,这个运算用CLZ指令加2就能获得同样的结果.我猜Doug Lea不这样写的原因可能是尽量减少各个平台的区别,或者纯粹是他懒得再分别写四种实现.