基于用户的协同过滤和皮尔逊相关系数

2012 年 11 月 05 日 isnowfy algorithm, web

Go to comment

推荐系统的经典算法就是协同过滤了，协同过滤算法有两种，一种是基于物品的，一种是基于用户的。从很多实验效果来看基于用户的协同过滤算法要好于基于物品的协同过滤算法。

那么简单来说基于物品的协同过滤算法是说我会推荐给你和你喜欢物品相似的物品，而基于用户的协同过滤算法是说我把和你相似的用户喜欢的东西推荐给你。为什么叫协同过滤呢，因为我们是利用用户的群体行为来作这些相似操作的。计算物品的相似的时候我们比较不同的人来对他打分来比较，同样计算用户相关性的时候我们就是通过对比他们对相同物品打分的相关度来计算的，我们来举个例子。

--------+--------+--------+--------+--------+
        |   X    |    Y   |    Z   |    R   |
--------+--------+--------+--------+--------+
    a   |   5    |    4   |    1   |    5   |
--------+--------+--------+--------+--------+
    b   |   4    |    3   |    1   |    ?   |
--------+--------+--------+--------+--------+
    c   |   2    |    2   |    5   |    1   |
--------+--------+--------+--------+--------+

a用户给X物品打了5分，Y打了4分，Z打了1分，同理b用户和c用户，那么很容易看到a用户和b用户非常相似，但是b用户没有看过R物品，那么我们就可以把和b用户很相似的a用户打分很高的R物品推荐给b用户，这就是基于用户的协同过滤。

ok，回到我们协同过滤的算法上，现在我们知道了基于用户的协同过滤需要比较用户的相关性，那么如何计算这个相关性呢，于是我们可以利用两个用户对于相同物品的评分来计算相关性。对于a，b用户而言，他们都对XYZ物品进行了评价，那么，a我们可以表示为(5,4,1)，b可以表示为(4,3,1)，经典的算法是计算把他们看作是两个向量，并计算两个向量间的夹角，或者说计算向量夹角的cosine值来比较，于是a和b的相关性为。

sim=5∗4+4∗3+1∗152+42+12√∗42+32+12√

这个值介于－1到1之间，越大，说明相关性越大。

到这里似乎cosine还是不错的，但是考虑这么个问题，用于用户间的差异，d用户可能喜欢打高分，e用户喜欢打低分，f用户喜欢乱打分。

--------+--------+--------+--------+
        |   X    |    Y   |    Z   |
--------+--------+--------+--------+
    d   |   4    |    4   |    5   |
--------+--------+--------+--------+
    e   |   1    |    1   |    2   |
--------+--------+--------+--------+
    f   |   4    |    1   |    5   |
--------+--------+--------+--------+

很显然用户d和e对于作品评价的趋势是一样的，所以应该认为d和e更相似，但是用cosine计算出来的只能是d和f更相似。于是就有皮尔逊相关系数（pearson correlation coefficient）。

sim=∑ni=1(Xi−Xˉ)∗(Yi−Yˉ)∑ni=1(Xi−Xˉ)2√∗∑ni=1(Yi−Yˉ)2√

pearson其实做的事情就是先把两个向量都减去他们的平均值，然后再计算cosine值。

最后让我们用实际数据来对比下cosine和pearson的效果吧。这里我们用到了movielens的数据，数据是1000多个用户对于1700个movie的超过10000的评分数据，数据已经分成多组，并且每组都是80%的训练数据和20%的测试数据。我们在训练数据上对于每个用户找出和他相似的20个用户，然后把当前用户没看过的这些用户的movie的评分加权和，然后选出5篇分数最高的作为推荐，然后把推荐出来的在测试数据上计算一个得分。代码如下。

 
    
      # -*- coding: utf-8 -*- 
     

         
     
 
      import  
      heapq 
     

         
     

       name =  
      'u1' 
     

         
     
 
      def get 
      (f 
      ): 
     

           ret =  
      { 
      } 
     

            
      for i  
      in  
      open 
      (f,  
      'r' 
      ): 
     

               tmp =  
      map 
      ( 
      int,  
      filter 
      ( 
      lambda x: 
      len 
      (x 
      ) 
      > 
      0, i. 
      split 
      ( 
      '\t' 
      ) 
      ) 
      ) 
     

                
      if tmp 
      [ 
      0 
      ]  
      not  
      in ret: 
     

                   ret 
      [tmp 
      [ 
      0 
      ] 
      ] =  
      { 
      } 
     

               ret 
      [tmp 
      [ 
      0 
      ] 
      ] 
      [tmp 
      [ 
      1 
      ] 
      ] = tmp 
      [ 
      2 
      ] 
     

            
      return ret 
     

         
     
 
      def cosine 
      (item1, item2 
      ): 
     

           sum0 =  
      sum 
      ( 
      map 
      ( 
      lambda x:x 
      [ 
      0 
      ] 
      *x 
      [ 
      1 
      ],  
      zip 
      (item1, item2 
      ) 
      ) 
      ) 
     

           sum1 =  
      sum 
      ( 
      map 
      ( 
      lambda x:x 
      *x, item1 
      ) 
      ) 
     

           sum2 =  
      sum 
      ( 
      map 
      ( 
      lambda x:x 
      *x, item2 
      ) 
      ) 
     

            
      return sum0/ 
      (sum1 
      ** 
      0.5 
      )/ 
      (sum2 
      ** 
      0.5 
      ) 
     

         
     
 
      def pearson 
      (item1, item2 
      ): 
     

           a1 =  
      ( 
      sum 
      (item1 
      ) 
      +0.0 
      )/ 
      len 
      (item1 
      ) 
     

           a2 =  
      ( 
      sum 
      (item2 
      ) 
      +0.0 
      )/ 
      len 
      (item2 
      ) 
     

           sum0 =  
      sum 
      ( 
      map 
      ( 
      lambda x: 
      (x 
      [ 
      0 
      ]-a1 
      ) 
      * 
      (x 
      [ 
      1 
      ]-a2 
      ),  
      zip 
      (item1, item2 
      ) 
      ) 
      ) 
     

           sum1 =  
      sum 
      ( 
      map 
      ( 
      lambda x: 
      (x-a1 
      ) 
      * 
      (x-a1 
      ), item1 
      ) 
      ) 
     

           sum2 =  
      sum 
      ( 
      map 
      ( 
      lambda x: 
      (x-a2 
      ) 
      * 
      (x-a2 
      ), item2 
      ) 
      ) 
     

            
      if  
      not sum1  
      or  
      not sum2: 
     

                
      return cosine 
      (item1, item2 
      ) 
     

            
      return sum0/ 
      (sum1 
      ** 
      0.5 
      )/ 
      (sum2 
      ** 
      0.5 
      ) 
     

         
     
 
      def get_sim 
      ( 
      user 
      ): 
     

           ret =  
      { 
      } 
     

            
      for i  
      in  
      user: 
     

               ret 
      [i 
      ] =  
      { 
      } 
     

                
      for j  
      in  
      user: 
     

                   itemset =  
      set 
      ( 
      user 
      [i 
      ]. 
      keys 
      ( 
      ) 
      ) 
      &set 
      ( 
      user 
      [j 
      ]. 
      keys 
      ( 
      ) 
      ) 
     

                   tmp1 =  
      map 
      ( 
      lambda x:x 
      [ 
      1 
      ],  
      filter 
      ( 
      lambda y:y 
      [ 
      0 
      ]  
      in itemset,  
      sorted 
      ( 
      user 
      [i 
      ]. 
      items 
      ( 
      ) 
      ) 
      ) 
      ) 
     

                   tmp2 =  
      map 
      ( 
      lambda x:x 
      [ 
      1 
      ],  
      filter 
      ( 
      lambda y:y 
      [ 
      0 
      ]  
      in itemset,  
      sorted 
      ( 
      user 
      [j 
      ]. 
      items 
      ( 
      ) 
      ) 
      ) 
      ) 
     

                    
      if  
      not  
      len 
      (tmp1 
      ): 
     

                       ret 
      [i 
      ] 
      [j 
      ] =  
      0 
     

                    
      else: 
     

                       ret 
      [i 
      ] 
      [j 
      ] = cosine 
      (tmp1, tmp2 
      ) 
     

            
      return ret 
     

         
     
 
      def get_re 
      ( 
      user, sim 
      ): 
     

           ret =  
      { 
      } 
     

            
      for i  
      in  
      user: 
     

               tmp =  
      filter 
      ( 
      lambda y:y 
      [ 
      0 
      ] 
      !=i,  
      heapq. 
      nlargest 
      ( 
      20, sim 
      [i 
      ]. 
      items 
      ( 
      ), key= 
      lambda x:x 
      [ 
      1 
      ] 
      ) 
      ) 
     

               tmp_res =  
      { 
      } 
     

                
      for j  
      in tmp: 
     

                    
      for k  
      in  
      user 
      [j 
      [ 
      0 
      ] 
      ]: 
     

                        
      if k  
      in  
      user 
      [i 
      ]: 
     

                            
      continue 
     

                        
      if k  
      not  
      in tmp_res: 
     

                           tmp_res 
      [k 
      ] =  
      0 
     

                       tmp_res 
      [k 
      ] += j 
      [ 
      1 
      ] 
      * 
      user 
      [j 
      [ 
      0 
      ] 
      ] 
      [k 
      ] 
     

               ret 
      [i 
      ] =  
      map 
      ( 
      lambda x:x 
      [ 
      0 
      ],  
      heapq. 
      nlargest 
      ( 
      5, tmp_res. 
      items 
      ( 
      ), key= 
      lambda x:x 
      [ 
      1 
      ] 
      ) 
      ) 
     

            
      return ret 
     

         
     
 
      def test_score 
      (test_data,  
      re 
      ): 
     

           score =  
      0 
     

            
      for i  
      in test_data: 
     

               u = test_data 
      [i 
      ] 
     

               r =  
      re 
      [i 
      ] 
     

               tmp =  
      0 
     

                
      for i  
      in r: 
     

                    
      if i  
      in u: 
     

                       tmp += u 
      [i 
      ] 
     

               score +=  
      (tmp 
      +0.0 
      )/ 
      len 
      (r 
      ) 
     

            
      return score/ 
      len 
      (test_data 
      ) 
     

         
     
 
      def main 
      ( 
      ): 
     

           data1 = get 
      (name+ 
      '.base' 
      ) 
     

           data2 = get 
      (name+ 
      '.test' 
      ) 
     

           sim = get_sim 
      (data1 
      ) 
     

            
      re = get_re 
      (data1, sim 
      ) 
     

            
      print test_score 
      (data2,  
      re 
      ) 
     

           
     

         
     
 
      if __name__ ==  
      '__main__': 
     

           main 
      ( 
      ) 
     
 
  

最后我们看看结果。

从图中可以看出，用pearson来计算用户相似来进行推荐的话，效果还是要好于cosine的。所以说基于用户的协同过滤还是用pearson来做用户相似是比较好的阿。

谈谈SVD和LSA

2012 年 11 月 23 日 isnowfy algorithm, 数学

Go to comment

首先SVD和LSA是什么呢，SVD全称是singular value decomposition，就是俗称的奇异值分解，SVD的用处有很多，比如可以做PCA(主成分分析)，做图形压缩，做LSA，那LSA是什么呢，LSA全称Latent semantic analysis，中文的意思是隐含语义分析，LSA算是topic model的一种，对于LSA的直观认识就是文章里有词语，而词语是由不同的主题生成的，比如一篇文章包含词语计算机，另一篇文章包含词语电脑，在一般的向量空间来看，这两篇文章不相关，但是在LSA看来，这两个词属于同一个主题，所以两篇文章也是相关的。

特征值特征向量

要谈到SVD，特征值和特征向量是需要首先交代的。具体内容可以在wiki上看，这里我做个简单的介绍。对于方阵M如果有

M∗v=λ∗v

v是个向量， λ 是个数，那么我们称v是M的特征向量， λ 是M的特征向量，并且我们可以对M进行特征分解得到

M=Q∗Λ∗Q−1

其中Q是特征向量组成的矩阵， Λ 是对角阵，对角线上的元素就是特征值。对于特征的几何理解就是矩阵M其实是一种线性变换，而线性变换对于向量的影响有两种，旋转和拉伸，而特征向量就是在这种线性变换下方向保持不变的向量，但是长度还是会作相应的拉伸，特征值就是拉伸的程度。

从另一个角度说如果我们取特征值比较大的几项，那么就是对原矩阵做了一种近似。

M≈Q1..k∗Λ1..k∗Q−11..k

这样我们就可以用更少的元素去近似的表示原矩阵，但是特征分解的限制比较多，比如要求矩阵必须是方阵

奇异值分解

wiki是个好东西，你要想深入了解的话，建议还是去看wiki。奇异值分解是将矩阵变成了这样的形式

M=U∗Σ∗VT

其中 Σ 依旧是对角阵，而U和V是正交矩阵正交矩阵是说 U∗UT=I 。

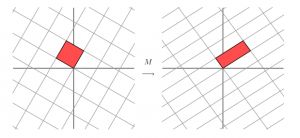
我们还是先回到矩阵是线性变换这个思路上。

如果我们用M去作用空间里的一组基，那么我们就会得到另一组基，如上图那样。那么我们旋转一下最初的一组基。

这样我们经过M的变换由一组正交基变换到了另一组正交基上面。也是也就是下面这样。

也就是我们有

M∗v1=σ1∗u1
M∗v2=σ2∗u2

并且对于任意一个向量x，我们有

x=v1∗(vT1∗x)+v2∗(vT2∗x)

于是我们可以得到

M∗x=M∗v1∗(vT1∗x)+M∗v2∗(vT2∗x)
M∗x=σ1∗u1∗(vT1∗x)+σ2∗u2∗(vT2∗x)
M=σ1∗u1∗vT1+σ2∗u2∗vT2
M=U∗Σ∗VT

恩，我们得到了和特征值和特征向量相似的东西，SVD分解出来的就是在M的线性变换下，正交基变换仍是正交基，而奇异值就是拉伸的程度。其实SVD和特征值和特征向量的关系还是很大的。

M∗MT=U∗Σ∗VT∗V∗ΣT∗UT
M∗MT=U∗Σ2∗UT

也就是说SVD求出的是 M∗MT 和 MT∗M 的特征向量。同样的得到这SVD分解这种形式后我们就可以利用他来对原数据进行降维操作。

这里我们分别将RBG矩阵进行SVD，左上角的是原图，其他的依次是取最大的100个，50个，20个，10个，5个奇异值做的近似图像。

 
     
       # -*- coding: utf-8 -*- 
      

          
      
 
       from scipy  
       import linalg, dot 
      
 
       from PIL  
       import Image 
      

          
      
 
       def main 
       (num= 
       5 
       ): 
      

            im = Image. 
       open 
       ( 
       'ai.jpg' 
       ) 
      

            pix = im. 
       load 
       ( 
       ) 
      

            ma =  
       [ 
       [ 
       ],  
       [ 
       ],  
       [ 
       ] 
       ] 
      

             
       for x  
       in  
       xrange 
       (im. 
       size 
       [ 
       0 
       ] 
       ): 
      

                 
       for i  
       in  
       xrange 
       ( 
       3 
       ): 
      

                    ma 
       [i 
       ]. 
       append 
       ( 
       [ 
       ] 
       ) 
      

                 
       for y  
       in  
       xrange 
       (im. 
       size 
       [ 
       1 
       ] 
       ): 
      

                     
       for i  
       in  
       xrange 
       ( 
       3 
       ): 
      

                        ma 
       [i 
       ] 
       [ 
       -1 
       ]. 
       append 
       (pix 
       [x, y 
       ] 
       [i 
       ] 
       ) 
      

             
       for i  
       in  
       xrange 
       ( 
       3 
       ): 
      

                u, s, v = linalg. 
       svd 
       (ma 
       [i 
       ] 
       ) 
      

                u = u 
       [:, :num 
       ] 
      

                v = v 
       [:num, : 
       ] 
      

                s = s 
       [:num 
       ] 
      

                ma 
       [i 
       ] = dot 
       (dot 
       (u, linalg. 
       diagsvd 
       (s, num, num 
       ) 
       ), v 
       ) 
      

             
       for x  
       in  
       xrange 
       (im. 
       size 
       [ 
       0 
       ] 
       ): 
      

                 
       for y  
       in  
       xrange 
       (im. 
       size 
       [ 
       1 
       ] 
       ): 
      

                    ret =  
       [ 
       ] 
      

                     
       for i  
       in  
       xrange 
       ( 
       3 
       ): 
      

                        tmp =  
       int 
       (ma 
       [i 
       ] 
       [x 
       ] 
       [y 
       ] 
       ) 
      

                         
       if tmp  
       <  
       0: 
      

                            tmp =  
       0 
      

                         
       if tmp  
       >  
       255: 
      

                            tmp =  
       255 
      

                        ret. 
       append 
       (tmp 
       ) 
      

                    pix 
       [x, y 
       ] =  
       tuple 
       (ret 
       ) 
      

            im. 
       show 
       ( 
       ) 
      

            im. 
       save 
       ( 
       'test.jpg' 
       ) 
      

          
      
 
       if __name__ ==  
       '__main__': 
      

            main 
       ( 
       ) 
      
 
   

如果对矩阵先进行归一化，再SVD就是PCA的形式了，这种形式可以用方差最大化或者误差最小化来求得，具体可以去看PCA相关的东西。所以和scturtle讨论了下直接SVD的意义，但是最后也没得出什么结论。。。

隐含语义分析

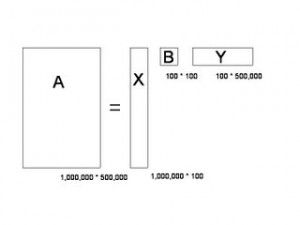
终于讲到最后的隐含语义分析了，首先我们构造文本和词语的矩阵，也就是对于矩阵来说每一个向量表示一篇文章，每个向量里就是单词的出现次数(更好的是每个是单词的tf/idf值，tf/idf不在赘述，具体可以看wiki)。那么SVD分解之后，我们就得到了降维的矩阵，就是下面这个样子

就是说原来我们有1000000篇文章，总共有500000个单词，我们保留最大的100个来做降维，于是现在我们可以这样理解，我们保留了100个主题，其中U是文章对应的主题分布，而V则是主题对应的词语的分布，这样，我们可以减少噪音，并且这样计算文章间的相关性也更加合理，并且可以把相关的单词聚合到一起。代码如下

 
     
       # -*- coding: utf-8 -*- 
      

          
      
 
       import  
       os 
      
 
       import  
       re 
      
 
       import  
       heapq 
      
 
       import  
       codecs 
      
 
       from  
       math  
       import log 
      
 
       from scipy  
       import linalg 
      

          
      
 
       import unigram_good_turing as seg 
      

          
      

        seg. 
       init 
       ( 
       ) 
      

          
      
 
       def tfidf 
       (docs 
       ): 
      

            doclen =  
       len 
       (docs 
       ) 
       +1.0 
      

             
       for doc  
       in docs: 
      

                wordtotal =  
       sum 
       (doc. 
       values 
       ( 
       ) 
       ) 
       +0.0 
      

                 
       for word  
       in doc: 
      

                    tf = doc 
       [word 
       ]/wordtotal 
      

                    idf = log 
       (doclen/ 
       ( 
       sum 
       ( 
       [word  
       in tmp  
       for tmp  
       in docs 
       ] 
       ) 
       +1 
       ) 
       ) 
      

                    doc 
       [word 
       ] = tf 
       *idf 
      

             
       return docs 
      

          
      
 
       def solve 
       (data 
       ): 
      

            re_zh, re_other =  
       re. 
       compile 
       (ur 
       "([\u4E00-\u9FA5]+)" 
       ),  
       re. 
       compile 
       (ur 
       "[^a-zA-Z0-9+#\n]" 
       ) 
      

            blocks = re_zh. 
       split 
       (data 
       ) 
      

             
       for item  
       in blocks: 
      

                 
       if re_zh. 
       match 
       (item 
       ): 
      

                     
       for i  
       in seg. 
       solve 
       (item 
       ): 
      

                         
       yield i 
      

                 
       else: 
      

                    tmp = re_other. 
       split 
       (item 
       ) 
      

                     
       for x  
       in tmp: 
      

                         
       if x  
       !=  
       '': 
      

                             
       pass 
      

          
      
 
       def show 
       (dic, p 
       ): 
      

            p =  
       heapq. 
       nlargest 
       ( 
       10,  
       enumerate 
       (p 
       ), key= 
       lambda x:x 
       [ 
       1 
       ] 
       ) 
      

             
       print  
       ' '. 
       join 
       ( 
       map 
       ( 
       lambda x:dic 
       [x 
       [ 
       0 
       ] 
       ], p 
       ) 
       ) 
      

          
      
 
       def main 
       ( 
       ): 
      

            names =  
       os. 
       listdir 
       ( 
       'text' 
       ) 
      

            dic =  
       { 
       } 
      

            cnt =  
       0 
      

            ma =  
       [ 
       ] 
      

             
       for name  
       in names: 
      

                data =  
       codecs. 
       open 
       ( 
       'text/'+name,  
       'r',  
       'utf-8' 
       ). 
       read 
       ( 
       ) 
      

                doc =  
       { 
       } 
      

                 
       for word  
       in solve 
       (data 
       ): 
      

                     
       if  
       not word  
       in dic: 
      

                        dic 
       [word 
       ] = cnt 
      

                        cnt +=  
       1 
      

                    tmp = dic 
       [word 
       ] 
      

                     
       if tmp  
       not  
       in doc: 
      

                        doc 
       [tmp 
       ] =  
       0 
      

                    doc 
       [tmp 
       ] +=  
       1 
      

                ma. 
       append 
       (doc 
       ) 
      

            ma = tfidf 
       (ma 
       ) 
      

            ret =  
       [ 
       ] 
      

             
       for item  
       in ma: 
      

                tmp =  
       [ 
       ] 
      

                 
       for i  
       in  
       xrange 
       (cnt 
       ): 
      

                     
       if i  
       in item: 
      

                        tmp. 
       append 
       (item 
       [i 
       ] 
       ) 
      

                     
       else: 
      

                        tmp. 
       append 
       ( 
       0 
       ) 
      

                ret. 
       append 
       (tmp 
       ) 
      

            u, s, v = linalg. 
       svd 
       (ret 
       ) 
      

             
       for i  
       in  
       xrange 
       ( 
       10 
       ): 
      

                show 
       ( 
       dict 
       ( 
       zip 
       (dic. 
       values 
       ( 
       ), dic. 
       keys 
       ( 
       ) 
       ) 
       ),  
       list 
       (v 
       [i 
       ] 
       ) 
       ) 
      

          
      
 
       if __name__ ==  
       '__main__': 
      

            main 
       ( 
       ) 
      
 
   

用来计算我博客的文章，可以得到如下的一些相关词语。

基于用户的协同过滤和皮尔逊相关系数

基于用户的协同过滤和皮尔逊相关系数

谈谈SVD和LSA

特征值特征向量

奇异值分解

隐含语义分析

你可能感兴趣的:(基于用户的协同过滤和皮尔逊相关系数)