LMSE理解
平均误差,就是指在等精度测量中,所测得所有测量值的随机误差的算术平均值。
均方值(mean-square),一般用它的另一种形式:均方根值(也就是高中物理里面的“有效值”)。 我们死抠“均方值”这3个字的字眼都把概念弄清楚了——先把各项平方,再求做算术平均。
例如:x、y、z 3项求均方值。均方值=(x^2+y^2+z^2)/3。
均方根值也称作有效值,它的计算方法是先平方、再算术平均、然后开方。——百度百科。也就是对均方值开根号。
均方根是一种求平均的方法。求平均有多种方法,算术平均、几何平均、均方根……
标准误差
在相同测量条件下进行的测量称为等精度测量,例如在同样的条件下,用同一个游标卡尺测量铜棒的直径若干次,这就是等精度测量。对于等精度测量来说,除了平均误差之外,还有一种更好的表示误差的方法,就是标准误差。
标准误差定义为各测量值误差(测量值-真实值)的平方和的平均值的平方根。故又称为均方误差。那么谁能知道真实值呢?实际上,真值是难于得到的,实际中,人们通常用两种方法来近似确定真值,并称之为约定真值。
一种方法是采用相应的高一级精度的计量器具所复现的被测量值来代表真值,
另一种方法是在相同条件下多次重复测量的算术平均值来代表真值。
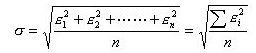
设n个测量值的误差为ε1、ε2……εn,则这组测量值的标准误差σ等于:
误差可以用绝度误差和相对误差来表示。绝对误差是分析结果与真值之差;相对误差是绝对误差和真值的百分比率。常用相对误差表示测定结果的准确度。
均方误差(Mean Squared Error, MSE)——各(绝对)误差的平方之和,再取平方根。
数理统计中均方误差是指参数估计值与参数真值之差平方的期望值,记为MSE。MSE是衡量“平均误差”的一种较方便的方法,MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。与此相对应的,还有均方根误差RMSE、平均绝对百分误差等等。——百度百科
标准差(Standard Deviation) ,也称均方差(mean square error),是各数据偏离平均数的距离的平均数,它是离均差平方和平均后的方根,用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。方差是波动大小,我认为,标准差数据较小,较易比较
最小均方误差就是求完均方值,还要加上约束条件,求出一个最小值来。
最小均方误差估计(Minimum mean-square error(缩写MMSE))是一种使均方误差最小的估计函数,其通常被称为最优估计。——wiki
附:——参考百度百科 百度百科——几何均值
geometric mean
几何平均值
如果有n个正数a1、a2、……、an,则几何平均值为这n个数乘积开n次方根的值,与代数(算术)平均值(a1+a2+ …… +an)/n不同。
如果有n个正数a1、a2、……、an,则几何平均值为这n个数乘积开n次方根的值,与代数(算术)平均值(a1+a2+ …… +an)/n不同。
当a,b,c...为正数时,他们的算术平均值大于等于他们的几何平均值。
比如,对于a,b,有几何平均值sqrt(axb)。