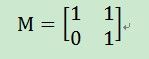矩阵奇异值分解及其应用
这篇论文是矩阵分析课上老师布置的一项作业,主要内容来自于http://www.ams.org/samplings/feature-column/fcarc-svd 这篇文章,经过自己的翻译整理后得到了这篇文章。这里并不是完全按照全文进行一字一句的翻译,添加了一些内容,删除了一些内容。
一、基础知识
1、特征值:
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:
这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式;
其中Q是这个矩阵A的特征向量组成的矩阵,∑是一个对角阵,每一个对角线上的元素就是一个特征值。
2、奇异值:
假设M是一个 mxn的矩阵,其中的元素全部属于域K,也就是实数域或复数域。如此则存在一个分解使得: ,其中U是mxm 阶酉矩阵,∑是半正定mxn 阶对角矩阵,而V* 即V的共轭转置,是nxn 阶酉矩阵。这样的分解就称为M的奇异值分解,∑对角线上的元素 ∑ij即为M的奇异值。
二、线性变换和奇异值分解的几何表示
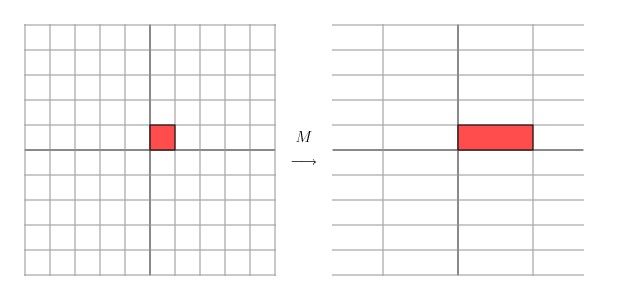
首先让我们来看一个简单的矩阵,例如下面这个两行两列的矩阵:
要知道一个矩阵其实就是一个线性变换,所以上面矩阵M其实对应于下面的线性变换:
因为这个矩阵M乘以一个点(x,y)的结果是:
也就等于把x坐标进行了横向拉伸。
易知上面的矩阵是对称的,所以这个变换是一个对x轴水平方向一个拉伸变换,当矩阵不是对称的时候,例如下面这个矩阵:
它描述的变换如下:
可以看到这一次的变换并不是水平方向的拉伸,而是向右上方45°角的拉伸。
上面这两个例子涉及的都是单一矩阵,接下来,我们来看看奇异值分解的几何表示,可以说,在几何上,奇异值分解的本质就是从一个正交网格到另一个正交网格的变换过程(注:这里只考虑欧式空间,未考虑酉空间的情况)。
考虑一组正交单位向量v1,v2和另一组正交向量Mv1,Mv2,如下图:
我们采用u1和u2作为Mv1,Mv2方向上的单位向量,并用σ1,σ2表示Mv1,Mv2的长度,这些值就称为M的奇异值。我们可以得到
Mv1=σ1u1
Mv2=σ2u2
针对一个向量x,在第一个坐标系中我们可以写成
这也就意味着
又因为
Mx可以变为
通常记为
其中U是u1和u2两个列向量构成的矩阵,∑是由σ1,σ2构成的对角矩阵,V是由v1,v2两个列向量构成的矩阵。
三、应用之一-数据压缩
奇异值分解可以被用来更有效的表示数据,假设我们想把下面这幅包含15X25个黑白像素点的图进行转换:
考虑到图中只有下面所示的三种类型的列,完全能够用一种紧凑的方式进行存储。
我们可以把这幅图用一个15 X 25的矩阵进行表述,一个位置上的元素如果是0则代表一个黑点,是1则代表一个白点。就这样,我们构造了一个包含375个元素的矩阵。
如果我们对M进行奇异值分解,我们将会发现只有三个非零的奇异值
σ1=14.72
σ2=5.22
σ3=3.31
因此,矩阵可以表示为
这也意味着我们有三个各包含15个元素的向量 ,同时还有三个各包含25个元素的向量 ,最后还有三个奇异值 。所以我们可以用123个元素而不是375个元素来表示这个矩阵。通过这种方式,奇异值分解发现了矩阵中的冗余信息并且提供了剔除冗余信息的方式。
四、应用之二-噪声消减
前一个例子告诉我们如何处理一个大多数奇异值都为0的矩阵。通常来说,较大的奇异值针对的都是我们感兴趣的信息。例如,假设我们用一个扫描仪把下面这幅图扫描到电脑中,但是在扫描过程中图像上出现了一些瑕疵(通常称为“噪声”)
我们用同样的方式进行处理:使用15 x 25的矩阵表示数据并且进行奇异值分解,得到的奇异值如下
σ1=14.15
σ2=4.67
σ3=3.00
…
σ15=0.05
很显然,前三个奇异值是最重要的,于是我们假设其他的奇异值都是因为图中存在噪声而产生的,可以做一个近似
这将会提示图像的质量
五、应用之三-数据分析
在我们收集数据时经常会发现噪声,无论我们的设备多么好,在测量值中总会包含错误。如果我们记得较大的奇异值对应着矩阵中重要的特征的话,那么使用奇异值分解来对刚刚收集到的数据进行学习处理就是理所当然了。
这里给一个例子,假设我们收集到的数据如下
我们可以取这些数据点并把它们放入到矩阵中
| -1.03 |
0.74 |
-0.02 |
0.51 |
-1.31 |
0.99 |
0.69 |
-0.12 |
-0.72 |
1.11 |
| -2.23 |
1.61 |
-0.02 |
0.88 |
-2.39 |
2.02 |
1.62 |
-0.35 |
-1.67 |
2.46 |
在进行奇异值分解后,我们能得到下面两个奇异值
σ1=6.04
σ2=0.22
可以看到第一个奇异值远远大于第二个,我们可以放心的假设较小的σ2是因为数据中存在噪声而产生的,而这个奇异值原本应该是0.在这种情况下,矩阵的秩为1,也就意味着所有的数据都位于ui定义的线上。
六、总结
由于奇异值良好的数学特性,奇异值分解不仅仅应用在主成分分析、图像压缩、数字水印和文章分类中,而且在信号分解、信号重构、信号降噪、数据融合、目标识别、目标跟踪、故障检测和神经网络等方面有很好的应用。用一句话来说,奇异值分解提供了一种极其有效的手段使得能够把线性代数的观点应用到实际运用中。
PS:今日上午考完了矩阵分析,这也给我学习生涯中最后一门纯数学课画上了句号。尽管魏丰老师告诉我们出去以后别告诉别人学过矩阵分析(因为课时太短内容讲的太浅),但这门课还是教会了我很多知识,从这篇文章中就能看到SVD的广泛应用,而SVD只不过是矩阵分析中一个比较典型的闪光点罢了。我记得大二的时候有北航的大牛告诉我线性代数在数据挖掘中应用极其广泛,看了吴军写的那本《数学之美》后发现确实如此。显然,数学绝对可以算是计算机IT界的奠基石,相信以后我会看到的更多,见识到更多的数学之美。