Spark MLlib — Word2Vec
Word2vec 是 Google 在 2013 年开源的一款将词表征为实数值向量的高效工具。能够将单词映射到K维向量空间，同时由于算法考虑了每个单词的上下文环境，因此词向量表示同时具有语义特性。本文对Word2Vec的算法原理以及其在spark MLlib中的实现进行了对应分析。（PS：第一次用latex打这么多公式，真是心累~）
1.背景知识
1.1 词向量
NLP中词向量通常有两种表示方式：
- One-hot Representaion
把每个单词按顺序编号，每个词就是一个很长的向量，向量的长度等于词表的大小，只有对应位置上的数字编号为1，其余位置为0.在实际应用中一般采用稀疏矩阵的表示方式。例如：
假设词表为{I, am, study, spark, machine, learning}
则若用稠密矩阵来表示单词spark，则为[0,0,0,1,0,0,0], 在Scala语法中就是Vectors.dense(0,0,0,1,0,0,0);
若用稀疏矩阵来表示单词spark，则为(6, 3, 1),这是一个三元组，6表示向量维度，3,1表示矩阵在3这个位置上的元素为1，其余位置元素均为0。在Scala语法中就是Vectors.sparse(6,(3),(1)) - Distributed Representaion
其基本思想是通过训练将每个词映射为K维实数向量，通过词之间的距离（例如cosine相似度、欧氏距离）来判断它们之间的语义相似度。Word2Vec就是使用这种Distributed Representaion的词向量表示方式。Word2Vec算法的一个附加输出就是输入语料文本中每个单词的Distributed Representaion词向量。
1.2 分类和逻辑回归
(1) 一般来说，回归不用再分类问题上，因为回归是连续模型，如果非要引入，可以使用logistic回归。logistic回归本质上仍是线性回归，只是在特征 X 到结果 y 的映射中加入了一层函数映射，先做线性求和再使用 σ(z) 作为假设函数来映射，将连续值映射到{0,1}上。logistic回归只能用于二分类，对于任意样本 x={x1,x2,...xn}T ，其评估函数为：
其中 σ(z)=11+e−z 就是sigmoid函数
(2) 选用sigmoid函数来做logistic回归的理由有：
平滑映射：能将 x∈(−∞,∞) 平滑映射到(0,1)区间
其导数具有如下特点：
σ′(z)=ddz(11+e−z)=e−z(1+e−z)2=11+e−z(1−11+e−z)=σ(z)(1−σ(z))(1.2)
(3) 使用logistic回归进行二分类，实际上是取阈值T=0.5，即使用如下判别公式：
y(x)={10hθ(x)≥0.5hθ(x)<0.5(1.3)
假设这里的二分类满足伯努利分布，也即
p(y=1|x;θ)p(y=0|x;θ)=hθ(x)=1−hθ(x)
也即:
p(y|x;θ)=(hθ(x))y(1−hθ(x))1−y(1.4)
(4)参数 θ 向量的求取方法通常为：假设训练集是独立同分布的，期待模型能在全部训练数据上预测最准，也就是求使其概率积最大 θ ，使用最大似然估计，其对数似然函数表示为：
L(θ)l(θ)=p(Y|X;θ)=∏i=1mp(y(i)|x(i);θ)=∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)=logL(θ)=∑i=1my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))(1.5)
(5)要求得使上面的似然函数 l(θ) 最大的 θ ，可使用牛顿上升法，即使用 θ:=θ+α∇θl(θ) 迭代公式来不断迭代直到收敛，其中
∇θjl(θ)=∑i=1m(y(i)×1hθ(x(i))+(1−y(i))×−11−hθ(x(i)))∂∂θj(hθ(x(i)))=∑i=1m(y(i)σ(θTx(i))−1−y(i)1−σ(θTx(i)))∂∂θj(σ(θTx(i)))
由公式(1.2)中对sigmoid函数的求导结果可进一步计算为:
∇θjl(θ)=(y(i)σ(θTx(i))−1−y(i)1−σ(θTx(i)))×σ(θTx(i))(1−σ(θTx(i)))∂∂θjθTx(i)=(y(i)(1−σ(θTx(i)))−(1−y(i))σ(θTx(i)))x(i)j=(y(i)−σ(θTx(i)))x(i)j=(y(i)−hθ(x(i)))x(i)j(1.6)
因此参数的迭代公式为
θ:=θ+α(y(i)−hθ(x(i)))x(i)j(1.7)
此处给出最大似然估计的推导过程，以便在后面Word2Vec模型参数的求解中可以直接使用
1.3 Huffman编码
哈夫曼编码是哈夫曼树的一个应用，哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的 路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+…+Wn*Ln), N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明哈夫曼树的WPL是最小的。
哈夫曼编码步骤：
(1) 对给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,…,Ti,…,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算 法，一般还要求以Ti的权值Wi的升序排列。）
(2) 在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。
(3) 从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。
(4) 重复二和三两步，直到集合F中只有一棵二叉树为止。
这里给出Spark Mllib中Word2Vec模型中构建Huffman构建哈夫曼树及哈夫曼编码的源码解析：
/*词典中单词的数据结构*/
private case class VocabWord(
var word: String, //分词
var cn: Int, //计数
var point: Array[Int], //存储路径,即经过得结点
var code: Array[Int], //记录Huffman编码
var codeLen: Int //存储到达该叶子结点,要经过的结点
)
private def createBinaryTree(): Unit = {
val count = new Array[Long](vocabSize * 2 + 1) //二叉树中所有的结点
val binary = new Array[Int](vocabSize * 2 + 1) //设置每个结点的Huffman编码：左1，右0
val parentNode = new Array[Int](vocabSize * 2 + 1)//存储每个结点的父结点
val code = new Array[Int](MAX_CODE_LENGTH) //存储每个叶子结点的huffman编码
val point = new Array[Int](MAX_CODE_LENGTH)//存储每个叶子结点的路径
var a = 0
while (a < vocabSize) {
count(a) = vocab(a).cn //初始化叶子结点，结点的权值即为词频
a += 1 //叶子结点编号为0~vocabSize-1与vocabHash中对分词的编号是一致的
}
while (a < 2 * vocabSize) {
count(a) = 1e9.toInt //初始化非叶子结点，结点权值为无穷大；非叶子结点编号为vocabSize ~ 2* vocabSize-1
a += 1
}
var pos1 = vocabSize - 1
var pos2 = vocabSize
var min1i = 0
var min2i = 0
a = 0
while (a < vocabSize - 1) { //构建Huffman树
if (pos1 >= 0) {
if (count(pos1) < count(pos2)) {
min1i = pos1
pos1 -= 1
} else {
min1i = pos2
pos2 += 1
}
} else {
min1i = pos2
pos2 += 1
}
if (pos1 >= 0) {
if (count(pos1) < count(pos2)) {
min2i = pos1
pos1 -= 1
} else {
min2i = pos2
pos2 += 1
}
} else {
min2i = pos2
pos2 += 1
}
count(vocabSize + a) = count(min1i) + count(min2i)
parentNode(min1i) = vocabSize + a
parentNode(min2i) = vocabSize + a
binary(min2i) = 1
a += 1
}
// 为词典中的每个单词计算其Huffman编码
var i = 0
a = 0
while (a < vocabSize) {
var b = a
i = 0
while (b != vocabSize * 2 - 2) {
code(i) = binary(b)
point(i) = b
i += 1
b = parentNode(b)
}
vocab(a).codeLen = i
vocab(a).point(0) = vocabSize - 2
b = 0
while (b < i) {
vocab(a).code(i - b - 1) = code(b)
vocab(a).point(i - b) = point(b) - vocabSize
b += 1
}
a += 1
}
}2. 模型
2.1 统计语言模型
传统的统计语言模型是表示语言基本单位(一般为句子)的概率分布函数，这个概率分布也就是语言的生成模型，一般语言模型可以使用各个单词的条件概率表示。假设 W=ωT1:={ω1,ω2,...,ωT} 表示由T个单词 ω1,ω2,...,ωT 按照顺序构成的一个句子，则 ω1,ω2,...,ωT 的联合概率为：
p(W)=p(ωT1)=p(ω1)⋅p(ω2|ω1)⋅⋅⋅p(ωT|ωT−11)(2.1)
其中的条件概率就是语言的模型参数，但是在实际中并不直接采用这种条件概率模型，因为在单词 ωT 的条件概率 p(ωT|ωT−11) 的计算就要考虑其之前的所有单词 ωT−11:={ω1,ω2,...,ωT−1} 。更一般的统计语言模型表示如下：
p(W)=p(ωT1)=∏t=1Tp(ωt|Context(ωt))(2.2)
其中 Context(ωt) 为单词 ωT 的上下文。根据上下文的不同，可以派生出不同的统计语言模型，例如：
- Context(ωt)=NULL 就表示上下文无关模型。该模型不考虑任何上下文信息，仅仅依赖于训练文本中的词频统计。
- Context(ωt)={ωt−n+1,ωt−n+2,...ωt−1} 就表示n-gram模型(或n-1阶马尔科夫模型)，即第n个词的出现只与前面的n-1个词相关，而与其它的任何词都不相关。一般n-gram模型优化的目标是最大log似然函数，即
l=∑t=1Tlogp(ωt|Context(ωt))
- 其余的还有决策树模型，神经网络模型，最大熵模型，条件随机场模型等。下面重点讲下在Word2Vec中用到的神经网络语言模型
2.2 神经网络语言模型
2.2.1 经典的三层神经网络：
假设输入层的结点个数为 n ，隐含层的结点个数为 l ，输出层的结点个数为 m 。输入层到隐含层的权重为 ωij ，隐含层到输出层的权重为 ωjk ，输入层到隐含层的偏置为 aj ，隐含层到输出层的偏置为 bk 。学习速率为 η ，激励函数为 g(x) 则上图中隐藏层输出 Hj 为：
Hj=g(∑i=1nwijxi+aj)(2.3)
输出层输出为：
yk=∑j=1lHjwjk+bk(2.4)
权值参数和偏置参数的计算可以采用最小化误差或最大似然估计等方法求解，这里不做详细介绍。关于激励函数的选取，常用的有之前介绍过的sigmoid函数以及tanh双曲正切函数等。
2.2.2 神经网络语言模型：
上图来自Bengio的《A Neural Probabilistic Language Model》，其中每个输入词被映射函数 C 映射为一个向量，即 C(wt−1) 表示 wt−1 的词向量。这里使用的激励函数是tanh，其输出也是一个向量，向量中的第i的元素表示概率 p(wt=i|wt−11) 。训练的目标依然是最大似然。
求解过程类似传统神经网络，只是一般神经网络的输入是已知的，不需要优化的，而在这里 x=C(wt−1,C(wt−2,...,C(wt−n+1) 也是需要优化的参数
2.3 Hierarchical Softmax
前面介绍的logstic回归可以实现对任意输入的二值分类(对任意输入的线性多项式求sigmod函数，再按阈值分类)。而更一般的情况可能是有K个分类，即目标输出 y∈{1,2,...,k} 。Softmax用于解决多值分类问题，关于logstic回归，一般线性回归以及Softmax回归的关系这里不展开，待有时间补充。
我理解的Hierarchical Softmax是一种基于Huffman树实现的多值分类模型。假设我们已经通过上面的1.3节构建了如下的Huffman树：
上图中Huffman树中的某个叶子结点对应词典 D 中的某个单词 w , 引入以下符号：
- pw ：从根结点出发到达词 w 对应的叶子结点对应的路径
- lw ：路径 pw 中包含结点的个数
- pw1,pw2,...,pwl ：路径 pw 中的 lw 个结点，其中 pw1 表示根结点， pwl 表示词 w 对应的叶子结点
- dw2,dw3,...,dwl∈{0,1} : 词 w 的Huffman编码，它由 lw−1 位0/1编码构成， dwj 表示路径 pw 中第j个结点对应的编码(根结点不对应编码)
- θw1,θw2,...,θwl∈Rm ：路径 pw 中非叶子节点对应的向量， θwj 表示路径 pw 中第j个非叶子节点对应的向量
以上的Huffman树其实就是任意一个单词 w 的上下文环境， p(w|Context(w)) 可以理解为在Huffman树的上下文环境中从根节点出发到达词 w 对应的叶子节点的概率。这个过程中经历了 lw−1 次分支(即路径上非叶子结点个数)，而每一次分支都可视为一次二分类。刚好可以利用每个非叶子结点的0/1的Huffman编码来进行分类。在Word2Vec中就是将Huffman编码为0的结点定义为正类，编码为1的结点定义为负类，即 Label(pwi)=1−dwi,i=2,3,...,lw 。
根据1.2节中的逻辑回归的知识可知，一个节点被分为正例的概率为 σ(xTw)=11+e−xTwθ ，被分为负例的概率为 1−σ(xTw) ，满足伯努利分布。对于从根节点出发到达“足球”这个叶子节点经历了4次二分类（图中的红色路径），每次分类结果的概率为：
- 第 1 次： p(dw2|xw,θw1)=1−σ(xTwθw1)
- 第 2 次： p(dw3|xw,θw1)=σ(xTwθw2)
- 第 3 次： p(dw4|xw,θw1)=σ(xTwθw3)
- 第 4 次： p(dw5|xw,θw1)=1−σ(xTwθw4)
从而可得：
p(w=足球|Context(足球))=∏j=25p(dwj|xw,θwj−1)
其实 p(w|Context(w)) 是一个多值分类的概率，因为单词w的取值范围为 w∈{喜欢，观看，巴西，足球，世界杯} 而借助Huffman树及Huffman编码将这个多值分类问题转化成了 lw−1 次独立同分布的二值分类问题。之后的求解过程完全类似于1.2节中用牛顿上升法求解最大似然估计的问题。
3. Word2Vec
Word2Vec总共有两种类型CBOW模型(Continuous Bag-of-Words Model)和Skip-gram模型(Continuous Skip-gram Model)，针对这两种模型分别给出了两种求解框架，基于Hierarchical Softmax 的求解框架和基于Negative Sampling的求解框架，共四种求解方法。Spark MLlib中Word2Vec采用的是Hierarchical Softmax+Skip-gram的求解方法，后面重点这种。
3.1 CBOW模型
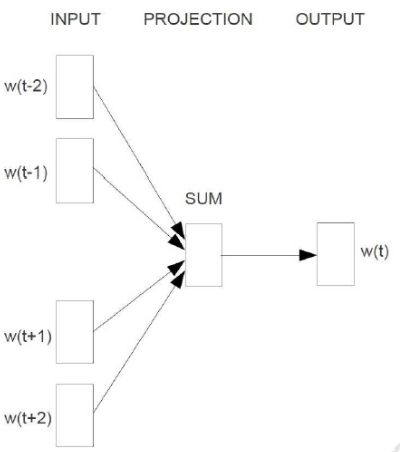
此模型类似于2.2.2节中的神经网络语言模型，已知词 wt 的上下文，预测词 wt 。从输入层到投射层所做的实际操作就是上下文向量的累加求和。CBOW去除了隐藏层，其输出层为树型结构。其目标对数似然函数为：
l=∑w∈Clogp(w|Context(w))(3.1)
其中，按照2.3节Hierarchical Softmax模型可知：
p(w|Context(w))=∏j=2lwp(dwj|xw,θwj−1)(3.2)
p(dwj|xw,θwj−1)=[σ(xTwθwj−1)]1−dwj⋅[1−σ(xTwθwj−1)]dwj(3.3)
回顾1.3节中逻辑回归的模型的最优化求解过程：对于模型 p(y|x;θ)=(hθ(x))y(1−hθ(x))1−y (公式1.4)求最大似然估计后，参数 θ 的迭代方程为 θ:=θ+α(y(i)−hθ(x(i)))x(i)j (公式1.7)。
显然对于公式(3.3)和公式(1.4)非常类似，只需令 x=xw;y=1−dwj;hθ(x)=σ(xTwθwj−1)]dwj ；带入公式(1.7)中即可得到对公式(3.3)做对数最大似然估计的参数迭代方程，即：
θwj−1:=θwj−1+α[1−dwj−σ(xTwθwj−1)]xw(3.4)
其中 α 为学习因子
之前提到过，Word2Vec和传统神经网络语言模型的区别在于其输入词向量 v(w˜) 也是要学习的，期迭代方程如下：
v(w˜):=v(w˜)+α∑j=2lw∂L(w,j)∂xw,w˜∈Context(w)(3.5)
3.2 Skip-gram模型
类似于COBOW模型，不过是在已知词 wt 的情况下，来预测其上下文。其中输入层到投影层是恒等投射，这个投影层也是多余的，该模型也没有隐藏层，输出层也是树型结构，其目标对数似然函数为：
l=∑w∈Clogp(Context(w)|w)(3.6)
其中：
p(Context(w)|w)=∏w∈Context(w)p(u|w)(3.7)
p(duj|v(w),θuj−1)=[σ(v(w)Tθuj−1)]1−duj⋅[1−σ(v(w)Tθuj−1)]duj(3.8)
该模型的最优化过程类似于COBOW，都是基于牛顿上升求取对数最大似然估计的过程，这里只给出参数迭代过程如下：
θuj−1v(w):=θuj−1+α[1−duj−σ(v(w)Tθuj−1)]v(w):=v(w)+α∑u∈Context(w)∑j=2lu∂L(w,u,j)∂v(w)(3.9)(3.10)
其中：
∂L(w,u,j)∂v(w)=[1−duj−σ(v(w)Tθuj−1)]θuj−1(3.11)
在Word2Vec中代码处理流程为：
/*构建词典*/
private def learnVocab[S <: Iterable[String]](dataset: RDD[S]): Unit = {
val words = dataset.flatMap(x => x)
vocab = words.map(w => (w, 1)) //为每个出现的分词设置计数为1
.reduceByKey(_ + _) //分词计数
.filter(_._2 >= minCount) //过滤掉词频小于minCount的分词
.map(x => VocabWord( //为每个分词建立VocabWord数据结构
x._1,
x._2,
new Array[Int](MAX_CODE_LENGTH),
new Array[Int](MAX_CODE_LENGTH),
0))
.collect()
.sortWith((a, b) => a.cn > b.cn) //按词频从大到小排序
vocabSize = vocab.length //词典元素的个数
require(vocabSize > 0, "The vocabulary size should be > 0. You may need to check " +
"the setting of minCount, which could be large enough to remove all your words in sentences.")
var a = 0
while (a < vocabSize) {
vocabHash += vocab(a).word -> a //构建hashMap<K:word,V:a>,这里实际上就是按照词频大小的顺序为分词编号，编号从0开始
trainWordsCount += vocab(a).cn //统计词典中所有分词的个数
a += 1 //编号值递增
}
logInfo(s"vocabSize = $vocabSize, trainWordsCount = $trainWordsCount")
}
def fit[S <: Iterable[String]](dataset: RDD[S]): Word2VecModel = {
learnVocab(dataset) //构建词典
createBinaryTree() //构建huffman树
val sc = dataset.context
//将构建的sigmoid函数查询表，词典以及Huffman树这些只读变量在集群中广播
val expTable = sc.broadcast(createExpTable())
val bcVocab = sc.broadcast(vocab)
val bcVocabHash = sc.broadcast(vocabHash)
// each partition is a collection of sentences,
// will be translated into arrays of Index integer
val sentences: RDD[Array[Int]] = dataset.mapPartitions { sentenceIter =>
// Each sentence will map to 0 or more Array[Int]
sentenceIter.flatMap { sentence =>
//找到每个单词在vocabHash中对应的序列值
val wordIndexes = sentence.flatMap(bcVocabHash.value.get)
//一条语句长度大于1000后，将被拆分为多个分组
wordIndexes.grouped(maxSentenceLength).map(_.toArray)
}
}
… …
//初始化叶子节点，分词向量随机设置初始化值
val syn0Global =
Array.fill[Float](vocabSize * vectorSize)((initRandom.nextFloat() - 0.5f) / vectorSize)
//初始化非叶子节点，参数向量设置初始化值为0
val syn1Global = new Array[Float](vocabSize * vectorSize)
var alpha = learningRate
for (k <- 1 to numIterations) {
val bcSyn0Global = sc.broadcast(syn0Global)
val bcSyn1Global = sc.broadcast(syn1Global)
val partial = newSentences.mapPartitionsWithIndex { case (idx, iter) =>
val random = new XORShiftRandom(seed ^ ((idx + 1) << 16) ^ ((-k - 1) << 8))
val syn0Modify = new Array[Int](vocabSize)
val syn1Modify = new Array[Int](vocabSize)
val model = iter.foldLeft((bcSyn0Global.value, bcSyn1Global.value, 0L, 0L)) {
case ((syn0, syn1, lastWordCount, wordCount), sentence) =>
var lwc = lastWordCount
var wc = wordCount
if (wordCount - lastWordCount > 10000) {
lwc = wordCount
// TODO: discount by iteration?
alpha =
learningRate * (1 - numPartitions * wordCount.toDouble / (trainWordsCount + 1))
if (alpha < learningRate * 0.0001) alpha = learningRate * 0.0001
logInfo("wordCount = " + wordCount + ", alpha = " + alpha)
}
wc += sentence.length
var pos = 0
while (pos < sentence.length) {
val word = sentence(pos)
val b = random.nextInt(window)
// Train Skip-gram
var a = b
while (a < window * 2 + 1 - b) {//此处循环是以pos为中心的skip-gram，即Context(w)中分词的向量计算
if (a != window) {
val c = pos - window + a //c 是以 pos 为中心，所要表征Context(w)中的一个分词
if (c >= 0 && c < sentence.length) {
val lastWord = sentence(c)//c是通过pos词得到的，即Huffman树的叶子结点，也就是lastWord
val l1 = lastWord * vectorSize
val neu1e = new Array[Float](vectorSize)//用来存储Context(w)中各分词向量对分词w的贡献向量值
// Hierarchical softmax
var d = 0
//以下循环体对应公式(3.9)
while (d < bcVocab.value(word).codeLen) {
val inner = bcVocab.value(word).point(d)
val l2 = inner * vectorSize
// Propagate hidden -> output
var f = blas.sdot(vectorSize, syn0, l1, 1, syn1, l2, 1)//syn0 * syn1 两向量相乘
if (f > -MAX_EXP && f < MAX_EXP) {
val ind = ((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2.0)).toInt
f = expTable.value(ind)
val g = ((1 - bcVocab.value(word).code(d) - f) * alpha).toFloat
blas.saxpy(vectorSize, g, syn1, l2, 1, neu1e, 0, 1)//neu1e = g * syn1 + neu1e
blas.saxpy(vectorSize, g, syn0, l1, 1, syn1, l2, 1)//syn1 = g * syn0 + syn1
syn1Modify(inner) += 1
}
d += 1
}
//以下一行即对应公式(3.10)
blas.saxpy(vectorSize, 1.0f, neu1e, 0, 1, syn0, l1, 1)//syn0 = 1.0f * neu1e + syn0
syn0Modify(lastWord) += 1
}
}
a += 1
}
pos += 1
}
(syn0, syn1, lwc, wc)
}
val syn0Local = model._1
val syn1Local = model._2
// Only output modified vectors.
Iterator.tabulate(vocabSize) { index =>
if (syn0Modify(index) > 0) {
Some((index, syn0Local.slice(index * vectorSize, (index + 1) * vectorSize)))
} else {
None
}
}.flatten ++ Iterator.tabulate(vocabSize) { index =>
if (syn1Modify(index) > 0) {
Some((index + vocabSize, syn1Local.slice(index * vectorSize, (index + 1) * vectorSize)))
} else {
None
}
}.flatten
}
val synAgg = partial.reduceByKey { case (v1, v2) =>
blas.saxpy(vectorSize, 1.0f, v2, 1, v1, 1)
v1
}.collect()
var i = 0
while (i < synAgg.length) {
val index = synAgg(i)._1
if (index < vocabSize) {
Array.copy(synAgg(i)._2, 0, syn0Global, index * vectorSize, vectorSize)
} else {
Array.copy(synAgg(i)._2, 0, syn1Global, (index - vocabSize) * vectorSize, vectorSize)
}
i += 1
}
bcSyn0Global.unpersist(false)
bcSyn1Global.unpersist(false)
}
newSentences.unpersist()
expTable.unpersist()
bcVocab.unpersist()
bcVocabHash.unpersist()
val wordArray = vocab.map(_.word)
new Word2VecModel(wordArray.zipWithIndex.toMap, syn0Global)
}4. Word2Vec应用
以下是使用Spark MLlib中Word2Vec的java应用代码
public class JavaWord2VecExample {
public static void main(String[] args) {
SparkSession spark = SparkSession
.builder()
.master("local")
.config("spark.sql.warehouse.dir", "file:///")
.appName("JavaWord2VecExample")
.getOrCreate();
// $example on$
// Input data: Each row is a bag of words from a sentence or document.
List<Row> data = Arrays.asList(
RowFactory.create(Arrays.asList("Hi I heard about Spark".split(" "))),
RowFactory.create(Arrays.asList("I wish Java could use case classes".split(" "))),
RowFactory.create(Arrays.asList("Logistic regression models are neat".split(" ")))
);
StructType schema = new StructType(new StructField[]{
new StructField("text", new ArrayType(DataTypes.StringType, true), false, Metadata.empty())
});
Dataset<Row> documentDF = spark.createDataFrame(data, schema);
// Learn a mapping from words to Vectors.
Word2Vec word2Vec = new Word2Vec()
.setInputCol("text")
.setOutputCol("result")
.setVectorSize(3)
.setMinCount(0);
Word2VecModel model = word2Vec.fit(documentDF);
/*打印词向量*/
Dataset<Row> words = model.getVectors();
for (Row row: words.collectAsList()) {
String word = row.getString(0);
Vector vector = (Vector) row.get(1);
System.out.println("Word: " + word + " => \nVector: " + vector + "\n");
}
/*打印输入语料中每一行句子对应的向量*/
Dataset<Row> result = model.transform(documentDF);
for (Row row : result.collectAsList()) {
List<String> text = row.getList(0);
Vector vector = (Vector) row.get(1);
System.out.println("Text: " + text + " => \nVector: " + vector + "\n");
}
// $example off$
spark.stop();
}
}程序执行结果如下：
Word: heard =>
Vector: [-0.053989291191101074,0.14687322080135345,-0.0022512583527714014]
Word: are =>
Vector: [-0.16293057799339294,-0.14514029026031494,0.1139335036277771]
Word: neat =>
Vector: [-0.0406828410923481,0.028049567714333534,-0.16289857029914856]
Word: classes =>
Vector: [-0.1490514725446701,-0.04974571615457535,0.03320947289466858]
Word: I =>
Vector: [-0.019095497205853462,-0.131216898560524,0.14303986728191376]
Word: regression =>
Vector: [0.16541987657546997,0.06469681113958359,0.09233078360557556]
Word: Logistic =>
Vector: [0.036407098174095154,0.05800342187285423,-0.021965932101011276]
Word: Spark =>
Vector: [-0.1267719864845276,0.09859133511781693,-0.10378564894199371]
Word: could =>
Vector: [0.15352481603622437,0.06008218228816986,0.07726015895605087]
Word: use =>
Vector: [0.08318991959095001,0.002120430115610361,-0.07926633954048157]
Word: Hi =>
Vector: [-0.05663909390568733,0.009638422168791294,-0.033786069601774216]
Word: models =>
Vector: [0.11912573128938675,0.1333899050951004,0.1441687047481537]
Word: case =>
Vector: [0.14080166816711426,0.08094961196184158,0.1596144139766693]
Word: about =>
Vector: [0.11579915136098862,0.10381520539522171,-0.06980287283658981]
Word: Java =>
Vector: [0.12235434353351593,-0.03189820423722267,-0.1423865109682083]
Word: wish =>
Vector: [0.14934538304805756,-0.11263544857501984,-0.03990427032113075]
Text: [Hi, I, heard, about, Spark] =>
Vector: [-0.028139343485236168,0.04554025698453188,-0.013317196490243079]
Text: [I, wish, Java, could, use, case, classes] =>
Vector: [0.06872416580361979,-0.02604914902310286,0.02165239889706884]
Text: [Logistic, regression, models, are, neat] =>
Vector: [0.023467857390642166,0.027799883112311366,0.0331136979162693]