Real-Time Rendering-第四章 Transforms（5）

4.6 Projections

在进行真正的场景渲染之前，必须把场景中的所有相关对象都投影到某个平面上或某种简单的包围体内。完成投影之后，就开始执行裁和渲染操作（见第2.3节）。

到目前为止，本章中的变换操作都没有使用到向量的第四个元素分量， w -分量。也就是说，点和向量在变换后依然为保持为原来的类型。另外， 4×4 矩阵的最下面一行元素始终为 (0  0  0  1) 。Perspective projection matrices（透视投影矩阵）则是这两种属性的一个例外情况：矩阵最下面一行包含了向量和点的操纵数，并且总是需要执行homogenization（齐次化）操作（即， w 分量通常不为 1 ，因此需要执行一次除以 w 的运算以获得非齐次的点）。而在本节首先会讨论的Orthographic projection（正交投影）是一种更简单的投影，也是很常用的。这种投影方式不会影响 w 分量。

在本节中，我们假设负 z -轴表示观察者的观看方向，y轴表示向上的方向，x轴表示向右的方向。这是一种右手坐标系。在一些书本和软件中，比如DirectX，使用左手坐标系，其中观察者的趋向对应于正 z -轴。这两坐标系表示方法同等有效，并且产生的最终结果是一样的。

4.6.1 Orthographic Projection（正交投影）

正交投影的特点之一是平行线在投影后依然保持平行。如下所示，矩阵 Po 是一个简单的正交投影矩阵，该投影不会改变坐标点的 x - 和 y -分量，只是简单地把 z -分量设置为零，即正交地投影到平面 z=0 ：

Po=⎛⎝⎜⎜⎜1000010000000001⎞⎠⎟⎟⎟.(4.59)

这种投影的效果如图4.16所示。显然，矩阵 Po 是不可逆的，因为行列式 |Po|=0 。换句话说，该变换从三维降到二维，并且没有办法取回丢弃的维度。使用这种正交投影产生的观察问题是，它会把 z 分量值为正的坐标点和 z 分量值为负的坐标点都投影到投影平面上。这种方法通常用于将坐标点的 z -值（以及 x -和 y -值）限制到特定的间隔范围内，比如说从 n （near plane）到 f （far plane）。这是下一个变换的目的。

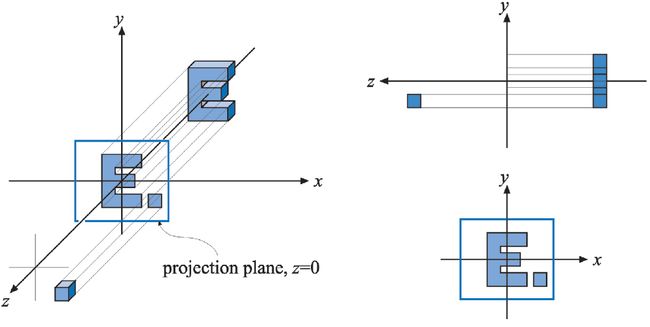
图4.16 由公式4.59生成的简单正交投影的三个不同视图。我们可以把这种投影看成是观察者沿着负 z -轴方向观察，这意味着投影只是简单地跳过 z -坐标（或设置为零）同时保持 x 和 y -坐标不变。注意在 z=0 两侧的物体都会投影到该投影平面上。

注：near平面也称为front plane或者hither，far平面也称为back plane或者yon。

用于执行正交投影变换的矩阵通常使用六元组 (l,r,b,t,n,f) 表示，分别表示left，right，bottom，top，near以及far平面。这个矩阵本质上是缩放和平移AABB（轴对齐包围盒；详见第16.2节中的定义），通过把6个平面放置到以原点为中心的轴对齐立方体的每一面中形成的。AABB的最小拐角是 (l,b,n) ，最大拐角为 (r,t,f) 。需要重点注意的是 n>f ，因为我们是沿着该空间体的负 z -轴方向观察。但是根据常识我们一般会认为near值应该是比far更小的数值。在OpenGL中观察方向也是朝向负 z -轴，但是在调用glOrtho函数创建正交投影矩阵时会把输入的near值表示为小于far值，然后在内部计算时对这两个值取反。另一种思考方式是OpenGL的near和far值是沿着观察方向（负 z -轴）的（正）距离值，而不是 z 视点坐标值。

在OpenGL中，轴对齐立方体的最小拐角为 (−1,−1,−1) ，最大拐角为 (1,1,1) ；而在DirectX中，对应的边界为 (−1,−1,0) 到 (1,1,1) 。该立方体称为canonical view volume（规范视图体），里面的坐标称为normalized device coordinates（NDC规范化设备坐标）。变换过程如图4.17所示。之所以要变换到canonical view volume内，是因为在这种坐标下裁剪操作更高效。

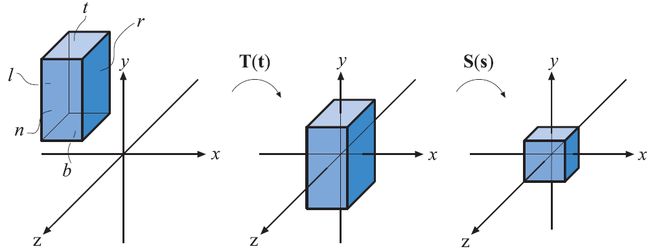
图4.17 在canonical view volume上变换轴对齐包围框。首先对左图的包围盒执行平移操作，使其中心与原点重合。然后对其进行缩放使其与canonical view volume具有相同的大小，如右图所示。

变换到canonical view volume之后，就根据该立方体对要渲染的几何图形的顶点进行裁剪。最后通过把单位正方形映射到屏幕，渲染位于立方体范围内的几何图形。这种正交变换矩阵如下所示：

Po=S(s)T(t)=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜2r−l00002t−b00002f−n0０001⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜100001000010−r+l2−t+b2−f+n21⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟.=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜2r−l00002t−b00002f−n0−r+lr−l−t+bt−b−f+nf−n1⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟.(4.60)

如该公式所示：矩阵 Po 可以写成一个平移矩阵 T(t) ，以及一个缩放矩阵 S(s) 的串联，其中 s=(2/(r−l),2(t−b),2/(f−n)) ， t=(−(r+l)/2),−(t+b)/2,−(f+n)/2) 。该矩阵是可逆的，即 P−1o=T(−t)S((r−l)/2,(t−b)/2,(f−n)/2) 。

注：当且仅当 n≠f ， l≠r 以及 t≠b 时是可逆的；否则，不存在可逆矩阵。

在计算机图形学中，经过投影变换之后通常使用左手坐标系—即对于视口来说， x -轴表示向右的方向， y -轴表示向上的方向， z -轴表示指向视口里面的方向。由于我们用于定义AABB的方式是far值小于near值，因此正交变换将始终包括一次镜像变换操作。使用这种方式，我们可以把原始AABBs看成与目标包围体，即canonical view volume的大小一致。于是AABB的坐标 (−1,−1,1) 对应于 (l,b,n) ， (1,1,−1) 对应于 (r,t,f) 。由此可以得到公式4.60

Po=⎛⎝⎜⎜⎜1000010000−100001⎞⎠⎟⎟⎟.(4.61)

这是一种镜像矩阵。正是通过这种镜像从右手观察坐标系（观察方向为负 z -轴）转换到左手normalized device coordinates（NDC）。

DirectX将 z -深度值映射到范围 [0,1] ，而不是OpenGL中使用的 [−1,1] 。在使用正交矩阵执行变换之后，通过应用一个简单的缩放和平移矩阵就可以实现这种转换，该矩阵为

Mst=⎛⎝⎜⎜⎜10000100000.50000.51⎞⎠⎟⎟⎟.(4.62)

因此在DirectX中使用的正交矩阵为

Po[0,1]=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜2r−l00002t−b00001f−n0−r+lr−l−t+bt−b−nf−n1⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟.(4.63)

通常使用矩阵的转置进行计算，因为在DirectXk中，通常使用行优先矩阵的表示方法。

4.6.2 Perspective Projection

比正交投影更有趣的一种变换是透视投影，在大多数计算机图形学应用程序中都会使用这种变换。在这种情况下，平行线在投影之后通常不再是平行的；相反，可能会在无穷远处聚集到单个点。透视投影更接近于我们感知真实世界的情况，即距离观察者越远的物体看起来越小。

首先，我们将提出一种有关透视投影矩阵的具有指导意义的推导过程，该投影矩阵把物体投影到平面 z=−d,d>0 上。从world space的推导到进一步简化对world-to-view变换的理解，最后推导出OpenGL中所使用的更规范的矩阵。

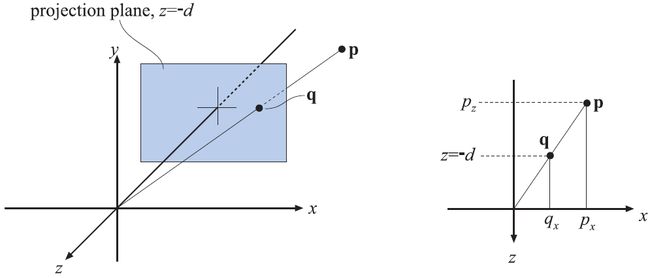
图4.18 用于推导透视投影矩阵的数学记号。其中点 p 投影到平面 z=−d,d>0 上，并产生投影点 q 。该投影是从相机所在位置的观察角度进行计算的，在这里为原点的位置。右图中显示了在推导过程中使用的针对 x -分量的相似三角形。

假设相机（视点）位于坐标原点，并且我们想要将点 p 投影到平面 z=−d,d>0 上，产生一个新的点 q=(qx,qy,−d) 。这种情形如图4.18所示。从该图中显示的相似三角形，由以下推导公式可以得到 q 的 x -分量：

qxpx=−dpz⟺qx=−dpxpz.(4.64)

q 的其他分量对应的表达式为 qy=−dpy/pz （计算过程与 qx 类似）， qz=−d 。与上述公式一起，可以推导出透视投影矩阵 Pp ，如下所示：

Pp=⎛⎝⎜⎜⎜10000100001−1/d0000⎞⎠⎟⎟⎟.(4.65)

通过公式4.66的简单验证可以确认该矩阵产生的透视投影的正确性：

q=Ppp=⎛⎝⎜⎜⎜10000100001−1/d0000⎞⎠⎟⎟⎟⎛⎝⎜⎜⎜⎜pxpypz1⎞⎠⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜pxpypz−pz/d⎞⎠⎟⎟⎟⎟⇒⎛⎝⎜⎜⎜⎜−dpx/pz−dpy/pz−d1⎞⎠⎟⎟⎟⎟.(4.66)

最后一步是基于整个向量除以 w -分量（在这种情况下该分量值为 −pz/d ）的事实，以便于在最后位置得到值1。由此生成的 z 值总是为 −d ，因为这是我们要投影的平面。

直观地说，很容易理解为什么齐次坐标允许投影。齐次化过程的一种几何解释是该操作把点 (px,py,pz) 投影到平面 w=1 上。

与正交变换一样，也有一个对应的透视变换，用于把视锥体变换为canonical view volume，而不是投影到一个具体的平面上（这种变换是不可逆的）。其中视锥体假定为起始于 z=n 处，并在 z=f 处结束，其中 0>n>f 。位于 z=n 处的矩形具有最小拐角值 (l,b,n) ，以及最大拐角 (r,t,n) 。如图4.19所示。

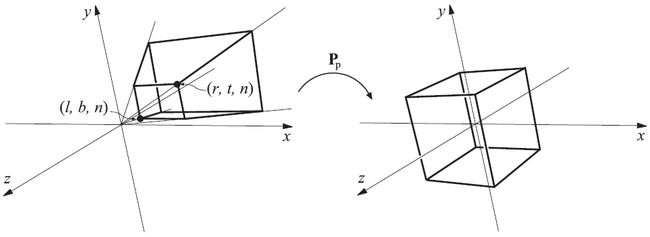
图4.19 使用矩阵 Pp 将视锥体变换成单位立方体，该立方体称为canonical view volume。

参数 (l,r,b,t,n,f) 确定了相机的视锥体。水平视域由左平面和右平面（由 l 和 r 确定）之间的角度决定。使用两样的方法，由顶平面和底平面（由 t 和 b 确定）之间的角度可以确定垂直视域。视域范围越大，通过相机能观察到的场景越多。通过设置 r≠−l 或者 t≠−b 可以创建非对称的平截头体。例如，非对称的平截头体可以用于表示立体视角（见第18.1.4节）以及CAVEs中[210]。

视域是提供给观察者一种场景感觉的重要因素。与计算机屏幕相比，人的眼睛本身具有物理上的视域范围。这种对应关系为

ϕ=2arctan(w/(2d)).(4.64)

其中 ϕ 表示视域， w 表示物体垂直于视线的宽度， d 是观察点到物体的距离。例如，一个21英寸的显示器大约是16英寸宽，而推荐的最小观察距离为25英寸[27]，由此产生一个35度的物理视域。依次计算，在12英寸远处，视域为67度；在18英寸处，则是48度；在30英寸为30度。这个公式也可以用于从相机镜头尺寸转换到视域范围，比如一个标准的50mm镜头用在35mm相机上（具有36mm宽的框架尺寸）可以得到 ϕ=2arctan(36/(2∗50))=39.6 度。

与物理设置相比，使用一个更窄的视域范围将会减少透视效果，因为场景中的观察者将会被放大。设置一个更宽的视域将使物体看起来变得扭曲（就像使用一个宽角度相机镜头），特别是靠近屏幕边缘的位置，并且会扩大附近物体的规模。但是，更宽的视域范围能够带给观察者一种物体变得更大，更令人印象深刻的感觉，并且具有向用户提供有关周围环境更多信息的优点。

使用公式4.68所示的透视变换矩阵可以把视锥体变换为一个单位立方体：

Po[0,1]=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜2nr−l00002nt−b00−r+lr−l−t+bt−bf+nf−n100−2fnf−n0⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟.(4.68)

注：其中 far平面也可以设置为无穷远处。有关具体形式，请阅读345页的公式9.8。

对一个点执行该变换操作，我们将会得到另一个点 q=(qx,qy,qz,qw)T 。点 q 的 w -分量 qw （通常情况下）为非零值并且不等于1。要得到投影后的点 p ，我们需要把每一个分量除以 qw ： p=(qx/qw,qy/qw,qz/qw,1)T 。从矩阵 Pp 中可以得出 z=f 映射到 +1 ，而 z=n 映射到 −1 。执行完投影变换之后，就会进行裁剪和齐次化（所有分量除以 w ）运算以得到normalized device coordinates（NDC）。

要获得在OpenGL中所使用的透视投影变换，与正交投影变换的理由一样，首先把 Pp 乘以 S(1,1,−1) 。这个乘法运算只是简单地把公式4.68中的矩阵 Pp 的第3列元素全部取反。在使用了该镜像变换操作之后，near和far的值就可以输入为正值，并且 0<n′<f′ ，正如人们在现实生活中通常感知的那样。但是这两个值仍然表示沿着世界坐标负 z -轴的距离，也就是朝着观察方向。作为参考，OpenGL的投影公式如下所示：

POpenGL=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜2n′r−l00002n′t−b00r+lr−lt+bt−b−f′+n′f′−n′−100−2f′n′f′−n′0⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟.(4.69)

注：因此为了验证该投影矩阵在 z -方向真正有效，我们可以把矩阵 POpenGL 乘以向量 (0,0,−n′,1)T 。由此得到的向量的 z -分量值将为 −1 。如果我们改用向量 (0,0,−n′,1)T ， z -分量值将为 +1 ，如期望的结果一致。对矩阵 P[0,1] 可以执行类似的测试。

有些API（比如DirectX）把near平面映射到 z=0 （而不是 z=−1 ），far平面映射到 z=1 。此外，DirectX还使用左手坐标系定义其投影矩阵。意味着DirectX沿着正 z -轴作为观察方向，并且把near和far值表示为正数。相应的，DirectX的投影公式如下所示：

Pp[0,1]=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜2n′r−l00002n′t−b00−r+lr−l−t+bt−bf′f′−n′100−f′n′f′−n′0⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟.(4.70)

DirectX在其文档中使用行优先的矩阵形式，因此该矩阵通常写成它的转置形式。

使用透视变换产生的一种影响是计算的深度值不会随着输入的 pz 值线性变化。例如，如果 n′=10 和 f′=110 （使用OpenGL术语），当 pz 位于负 z -轴方向的60个单位长度时（即，near和far的中间点），normalized device coordinate的深度值为0.833，而不是0。图4.20中显示了改变near平面到原点的距离产生的影响结果。near和far平面到原点的距离会影响 Z-buffer 的精度。在第18.1.2节中我们将会进一步讨论由此带来的影响。

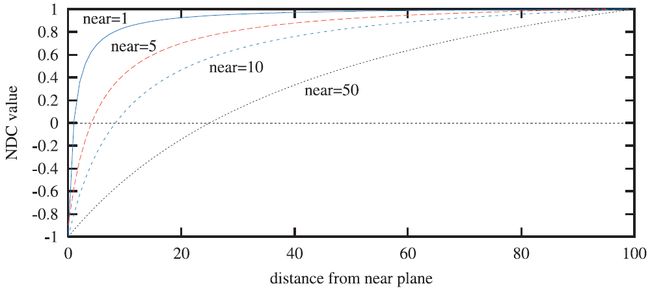
图4.20 改变 near平面到原点的距离产生的不同效果。其中 f′ 和 n′ 之间的距离始终固定为100。随着 near平面与原点的距离越近，越接近于 far平面的点能够使用的normalized device coordinate depth space 的范围越小。这会导致在更远距离处的 Z-bffer 的精度更低。

Further Reading and Resources

以一种轻松的方式建立对矩阵的直观理解，最好的书籍之一是 Farin 和 Hansford 的 The Geometry Toolbox[333]。另一本非常实用的书是Lengyel的 Mathematics for 3D Game Programming and Computer Graphics [761]。从不同的角度来讲，大量计算机图形课本，比如 Hearn 和 Baker [516]，Shirley [1172]，Watt 和 Watt [1330]，以及 Foley 等人[348,349]所编写的书籍中也包含有基本的矩阵知识。在Graphics Gems系列书籍中[36,405,522,667,982]讲解了各种变换相关的算法，并在线提供了各种变换的实现代码。 Golub 和 Van Loan 的 Matrix Computations[419]是一本值得认真研究通用矩阵技术的入门书籍。参考http://www.realtimerendering.com/网站，上面包含了各种不同的变换操作以及四元数的代码。关于skeleton-subspace deformation/vertex blending 以及 shape interpolation 的更多信息，请阅读 Lewis 等人的SIGGRAPH论文[770]。

Hart 等人[507] 和 Hanson [498]提供了四元数的可视化。Pletinckx 和 Schlag [1126]提出了在一组四元数之间进行平滑插值的不同方法。 Vlachos 和 Isidoro [1305]推导出了关于四元数的 C2 插值公式。有关四元数插值的主要问题是如何沿着一条曲线计算一致的坐标系。Dougan已经解决该问题[276]。

Alexa [16]和Lazarus＆Verroust [743]提出了关于各种不同的morphing技术的研究结果。