2014年山东省第五届ACM--angry_birds_again_and_again
Time Limit: 2000MS Memory limit: 65536K
题目描述
The problems called "Angry Birds" and "Angry Birds Again and Again" has been solved by many teams in the series of contest in 2011 Multi-University Training Contest.
This time we focus on the yellow bird called Chuck. Chuck can pick up speed and distance when tapped.
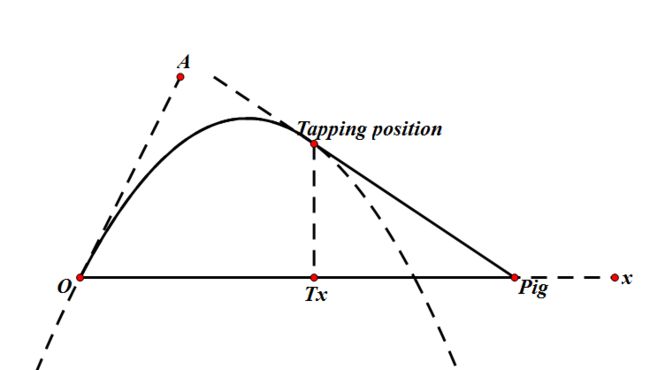
You can assume that before tapped, Chuck flies along the parabola. When tapped, it changes to fly along the tangent line. The Chuck starts at the coordinates (0, 0). Now you are given the coordinates of the pig (Px, 0), the x-coordinate of the tapping position (Tx) and the initial flying angle of Chuck (α).
∠AOx = α
Please calculate the area surrounded by Chuck’s path and the ground.(The area surrounded by the solid line O-Tapping position-Pig-O)
The first line contains only one integer T (T is about 1000) indicates the number of test cases. For each case there are two integers, px tx, and a float number α.(0 < Tx ≤ Px ≤ 1000, 0 < α < ) .
One line for each case specifying the distance rounded to three digits.
示例输入
1
2 1 1.0
示例输出
0.692
来源
2014年山东省第五届ACM大学生程序设计竞赛
题意:已知点tx、px坐标与∠AOX,求实线围成的面积。
思路:设抛物线方程为y=ax^2+bx+c;因为抛物线过原点,则c=0,又已知过原点的切线的斜率(tan(∠AOX)),对抛物线方程求导再结合点tx,可求出a,b;最后对抛物线方程从0到tx积分,再加上三角形面积。。
以下AC代码:
#include<stdio.h>
#include<math.h>
int main ()
{
int t;
double area1,area2;
double ang;
int px,tx,l;
double a,b,c;
scanf("%d",&t);
while(t--)
{
scanf("%d%d%lf",&px,&tx,&ang);
l=px-tx;
b=tan(ang);
a=(l*b*1.0+b*tx*1.0)/(tx*tx*1.0+2*l*tx*1.0);
c=-1.0*a*tx*tx+b*tx*1.0;
area2=(-1.0/3)*a*tx*tx*tx*1.0+1.0/2*b*tx*tx+(px-tx)*c*1.0/2;
printf("%.3lf\n",area2);
}
return 0;
}