【软考】——数制转换

【背景】

      软考的学习一个阶段一个阶段有条不紊地进行着，见识了软考需要学习的内容，才知道软件设计师中级职称是有它的含金量的，集数据库、操作系统、网络、软工等各家之大成，各方面的知识汇集与于一身，在进行软考的过程中，想想都觉得好兴奋，携着这份热情，路上的小风小浪都会是我们通向新的方向上的垫脚石，让我们站的更高，看的更远，那么随我来学习进制的转换吧。

【由来】

     

【不同进制数的特点】

                基数：一个数值所使用数码（数符）的个数。

                数符：也叫数码，一个进制中表示数值大小的不同数字符号。

进位制	二进制	八进制	十进制	十六进制
运算规则	逢2进1（加法运算） 借1当2（减法运算）	逢8进1（加法运算） 借1当8（减法运算）	逢10进1（加法运算） 借1当10（减法运算）	逢16进1（加法运算） 借1当16（减法运算）
基数	2	8	10	16
数符	0   1	0  1   2  3  4  5  6  7	0  1  2  3  4  5  6 7  8   9	0  1  2  3  4  5   6  7  8  9   A  B   C  D  E  F
简码表示	在二进制数据后加英文字母“B”	在八进制数据后加英文字母“O”,有时候会加“Q”	在十进制数据后加英文字母：“D”   或省略	在十六进制数据后加英文字母“H”/在十六进制数据前加“0x”
举例	1011-1011B	712-712O/712Q	123-123D或者123	3A4-3A4H/0x3A4

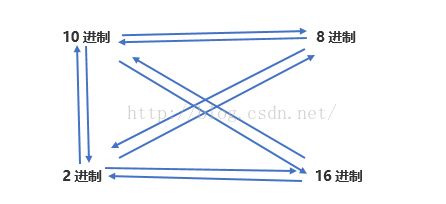
【进制的转换】

      

       权位法：将数值按权位展开之后计算该多项式之和

       余数法：将数值除以基数,整数部分除基数取余，小数部分乘基数取整。

•   R进制转十进制：

               对于任意一个n位整数和m位小数的R进制数D，均可按权展开

       D的表示形式：D_nD_n-1D_n-2…D₂D₁D₀.D_-1D_-2…D_-m

       D=Dn-1Rn-1+Dn-2Rn-2+Dn-3Rn-3+…+D2R2+D1R1+D0+D-1R-1+D-2R-2+…+D-mR-m

        Eg:  十进制数234.5→ 十进制数；二进制数10100.01→ 十进制数

     _{10100 . 01(2)=1*2⁴13*2²+1*2^-2} 

•  十进制转R进制；

       _{取整数部分和小数部分分别转换}

       _{整数部分的转换规则：除以基数取余，直至商为0，将所得余数用倒序排列。}

       _Eg:   

               ²⁶₍₁₀₎^{→（ ？）}_（2）

  ²⁶ ₍₁₀₎ ^{→ （ 11010）} _（2）

           

      小数部分的转换规则：乘R取整，知道小数部分为零或达到要求的精度，所得积用顺序排序。

           Eg:^0.56_{(10) 要求精确到小数点后5位}

                 所以     ^（26.56）₁₀^{=（11010.100011）}

•  二进制数转为八进制数；

      每3位二进制数表示1位八进制数

      方法：首先从小数点开始分别向左和向右把整数及小数部分每3位分成一组。若整数最高位不足3位，则在其最左边加0补足3位。若小数最高位的一组不足3位，则在其最右边加0补足3位。然后进行译码，把每一个3位二进制数译成一个一位八进制数。

Eg:把^{（1011.10101）}_{2 转换为八进制数}

• 八进制转换为二进制；

    每1位八进制数表示3位二进制数

Eg: 把^(13.52)₈转换为二进制数

     

• 十六进制和二进制的转换；

   和上述八进制与二进制的转换同理，任意一位十六进制数都可以用一个四位二进制数来表示，这里就不再详述。

【小结】

         

        如有不足，欢迎大家多多提建议~~