算法系列—动态规划法
一、基本概念:
1.自顶向下(又称记忆化搜索、备忘录):基本上对应着递归函数实现,从大范围开始计算,要注意不断保存中间结果,避免重复计算
2.自底向上(递推):从小范围递推计算到大范围
动态规划的重点:递归方程+边界条件
三、算法特点:
1. 动态规划任何一个i+1阶段都仅仅依赖i阶段做出的选择,而与i之前的选择无关。但是动态规划不仅求出了当前状态的最优值,而且同时求出了到中间状态的最优值;
2. 缺点:空间需求大;
1.最优化原理(最优子结构性质)一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
2.无后效性 将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。
3.子问题的重叠性 动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。for(j=1; j<=m; j=j+1) // 第一个阶段
xn[j] = 初始值;
for(i=n-1; i>=1; i=i-1)// 其他n-1个阶段
for(j=1; j>=f(i); j=j+1)//f(i)与i有关的表达式
xi[j]=j=max(或min){g(xi-1[j1:j2]), ......, g(xi-1[jk:jk+1])};
t = g(x1[j1:j2]); // 由子问题的最优解求解整个问题的最优解的方案
print(x1[j1]);
for(i=2; i<=n-1; i=i+1)
{
t = t-xi-1[ji];
for(j=1; j>=f(i); j=j+1)
if(t=xi[ji])
break;
}
动态规划算法可以求解很多问题,比如矩阵乘法、最长公共子序列、构造最优二叉查找树等,现就著名的最长公共子序列问题,采用动态规划法分析之。
相关定义:
子序列:若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xij.
公共子序列:给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列.
最长公共子序列:给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列.
如:序列ABCDEF和ADFGH的最长公共子序列为ADF
注意:最长公共子串(Longest Common Substirng)和最长公共子序列(Longest Common Subsequence,简称LCS)的区别为是最长公共子串的串是一个连续的部分,而最长公共子序列则是从不改变序列的顺序,而从序列中去掉任意的元素而获得新的序列;通俗的说就是子串中字符的位置必须是连续的而子序列则可以不必连续。
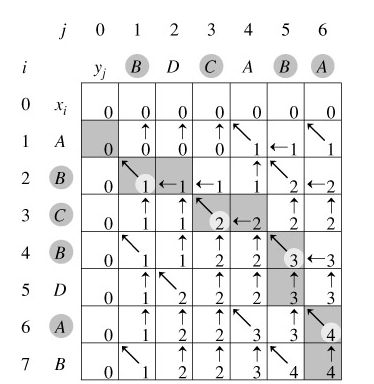
问题描述:给定2个序列X={A,B,C,B,D,A,B}和Y={B,D,C,A,B,A},找出X和Y的最长公共子序列.(转载1)(转载2) 算法分析思路:
1.分析最优子结构性质:
设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
(1)若xm=yn,则zk=xm=yn,且z1,z2,…, zk-1是否为x1,x2,…,xm-1和y1,y2,…,yn-1的最长公共子序列.
(2)若xm≠yn且zk≠xm,则Z是x1,x2,…,xm-1和Y的最长公共子序列.
(3)若xm≠yn且zk≠yn,则Z是X和y1,y2,…,yn-1的最长公共子序列.
由此可见,2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列.因此,最长公共子序列问题具有最优子结构性质.当问题具有最优子结构性质和子问题重叠性质时就可以用动态规划算法解决该问题.
2.由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系.用c[i][j]记录序列和的最长公共子序列的长度.其中,Xi={x1,x2,…,xi},Yj={y1,y2,…,yj}.当i=0或j=0时,空序列是Xi和Yj的最长公共子序列.故此时C[i][j]=0.其它情况下,由最优子结构性质可建立递归关系如下:
回溯输出最长公共子序列过程:
算法分析:由于每次调用至少向上或向左(或向上向左同时)移动一步,故最多调用(m + n)次就会遇到i = 0或j = 0的情况,此时开始返回。返回时与递归调用时方向相反,步数相同,故算法时间复杂度为Θ(m + n)。
算法实现:
//LCS 最长公共子序列
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 100
void LCS(char *x, char *y,int x_len, int y_len, int common_len[][MAX], int b[][MAX])
{
//common_len[i][j]存储的是x的第i位与有的第j位的公共子序列的长度
//b[i][j] 记录获得common_len[i][j]的路径:分别为0 -1 1,便于回溯输出公共子串
int i,j;
for (i = 0; i < x_len; i++)
common_len[i][0] = 0;
for (j = 0; j < y_len; j++)
common_len[0][j] =0;
for (i = 1; i <= x_len; i++)
{
for (j = 1; j <= y_len; j++)
{
if (x[i-1] == y[j-1]) //从零开始存储,所以第i位为x[i-1]
{
common_len[i][j] = common_len[i-1][j-1] + 1;
b[i][j] = 0;
}
else if (common_len[i-1][j] >= common_len[i][j-1])
{
common_len[i][j] = common_len[i-1][j];
b[i][j] = -1;
}
else
{
common_len[i][j] = common_len[i][j-1];
b[i][j] = 1;
}
}
}
}
void backtrack(int i, int j,int b[][MAX], char *x)
{
if (0 == i || 0 == j)
return;
else if (0 == b[i][j])
{
backtrack(i-1,j-1,b,x);
printf("%c",x[i-1]);
}
else if(-1 == b[i][j])
{
backtrack(i-1,j,b,x);
}
else
{
backtrack(i,j-1,b,x);
}
}
int main()
{
int x_len,y_len;
char x[MAX] = "ABCBDAB";
char y[MAX] = "BDCABA";
int common_len[MAX][MAX];
int b[MAX][MAX];
x_len = strlen(x);
y_len = strlen(y);
LCS(x,y,x_len,y_len,common_len,b);
backtrack(x_len,y_len,b,x);
printf("\n");
return 0;
}
转载请注明出处:http://blog.csdn.net/daijin888888/article/details/53115323