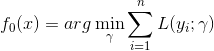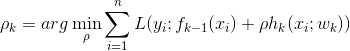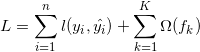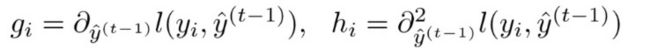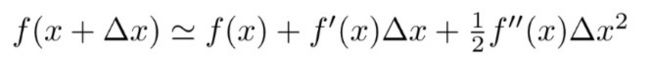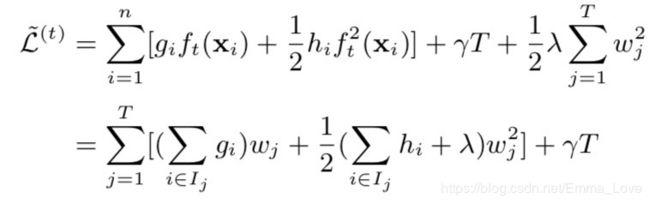机器学习知识点总结 - xgboost, GBDT
GBDT和XGBoost在工业界和竞赛界有着广泛的应用。虽然使用起来并不难，但若能知其然也知其所以然，则会在使用时更加得心应手。本文主要是根据对陈天奇大神的PPT和原始论文的学习，梳理一下GBDT和XGBoost的“知识点”。
首先我们先列出CART，GB，GBDT和XGBoost之间的关系。
- CART是分类与回归树（Classification and Regression Trees），是决策树的一种，既能做分类，又能做回归。在分裂过程中会用Gini值作为纯度的评估标准。
- Gradient Boosting（GB）算法：是Boosting算法的一种，具体稍后介绍。
- GBDT（Gradient Boosting Decision Tree）：正如其名字一样，GBDT是GB与DT的集合，这里面GB代表Gradient boosting算法，DT代表decision tree算法，GBDT就是使用CART作为基学习器的GB算法。
- XGBoost：xgboost扩展和改进了GDBT，xgboost算法更快，准确率也相对高一些。
接下来，我们将详细的介绍GB，GBDT和XGBoost算法，CART将放到决策树一块进行介绍。
陈天奇大神的PPT：《Introduction to Boosted Trees》
原始论文：《XGBoost: A Scalable Tree Boosting System》
目录
0. CART
1. 梯度增强 Gradient Boosting (GB)
2. GBDT
3. XGBoost
3.1 XGBoost的学习过程
3.2 XGBoost推导
3.3 如何构建树结构 —— 分裂节点的算法？
3.3.1 Greedy Learning of the tree
3.2.2 Approximate Algorithm
4. 针对稀疏数据的算法——缺失值处理
5. XGBoost减小过拟合的方式
6. XGBoost的优点
7. XGBoost vs. GBDT
0. CART
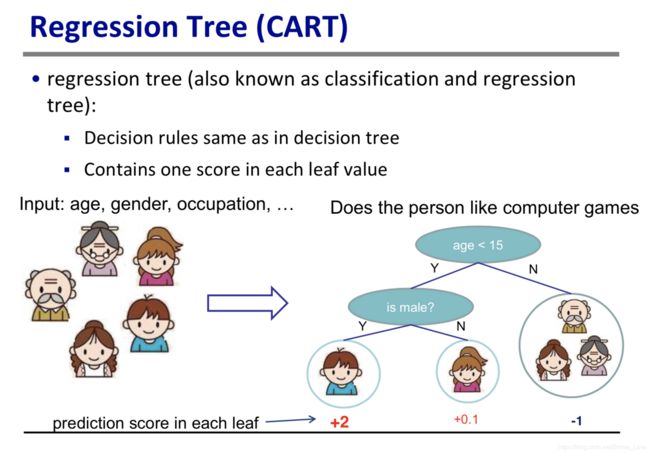
CART（Classification and Regression Trees，分类与回归树，简称回归树）也是一种树模型，它既能解决分类问题，也能处理回归问题。
参照陈大神的PPT，对回归树有一个直观的感受。
可以看到，回归树与分类树有很多相似之处，例如：都是树形结构，每个非叶子节点可以代表一个条件判断。
与分类树不同的是，
- 分类树叶子节点给出的是类别标签；而回归树的叶子节点会给出一个score，根据这个得分可以进行分类或者回归。
- 回归树在节点划分的过程中，不适用信息熵或Gini指数作为特征好坏的评估标准，而是使用一种启发式的操作，利用最小化均方差来进行评估。下面给出一个对比：
| 分类树 | 回归树 | ||
| 以C4.5为例，在分裂出新的分枝时，采用Gini指数评估样本纯度。 具体过程如下：
|
与分类树不同的是，回归树在分裂出新的分枝时，不使用Gini指数，而是使用最小化均方差进行衡量特征的好坏，即： 其中， 那么：最优切分变量j和最优切分点s的求解可以用下面的式子进行：
其中， 具体流程：
|
的结果的”是“与”否“划分为两个部分，利用下述公式进行计算。
特征A以及该特征
代表划分到该划分单元上的样本集合，
是每个划分单元的预测值 —— 即该单元内每个样本点的值的均值：
和
是被划分后的两个区域。
：
1. 梯度增强 Gradient Boosting (GB)
GB算法是Boosting算法的一种。
Boosting算法的学习过程采用的思想是Additive Manner（加法效应），即：迭代生成多个（K个）弱学习器，然后将弱模型的结果相加，其中后面的模型是基于前面的模型的效果生成的，模型间的关系以及最后的预测结果如下：
 |
公式（1.1） |
 |
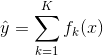公式（1.2） |
可以看到，Boosting算法是通过一系列的迭代来优化分类结果，每迭代一次引入一个新的弱分类器，来克服现在已经存在的弱分类器组合的shortcomings，即：每一次迭代都致力于减少偏差。
- Adaboost vs. Gradient Boosting
Adaboost和Gradient Boosting是两种boosting算法，他们的区别就在于如何选择
,即：采用何种策略来克服前面已有的shortcoming。
Adaboost采取的策略是在每一次新的迭代中，增加上一轮分类错误的样本的权重以提高对这些样本的关注程度。
Gradient Boosting算法在迭代的时候将负梯度作为上一轮基学习器犯错的衡量指标，在下一轮学习中通过拟合负梯度来纠正上一轮犯的错误。
| Question：为什么可以采用负梯度作为衡量指标呢？ Answer： 这就需要结合梯度下降方法进行分析啦。机器学习的学习过程就是通过优化算法找到使得损失函数
GB算法的学习过程也是基于Additive Manner（加法模型）的，因此在第k步的目标是最小化损失函数
对比公式（1.1）和（1.4），可以发现若将
负梯度也被称为“响应 (response)”或“伪残差 (pseudo residual)”。残差 |
最小的参数
。梯度下降方法的更新公式：
作为参数，则可以同样适用梯度下降法：
拟合前一轮模型损失函数的负梯度，就是通过梯度下降法最小化
。由于
越大，表明前一轮学习器
相差较大，那么下一轮学习器通过拟合残差或负梯度，就能纠正之前的学习器犯错较大的地方。- GB算法的步骤：
| step 1. 初始化： step 2. for k = 1 to K: (a). 计算负梯度： (b). 通过最小化平法误差，用基学习器
(c). 使用line search确定步长 (d). 求得 step 3. 输出 |
：
，以使得
最小:
:
2. GBDT
GBDT（Gradient Boosting Decision Tree）是以决策树（CART）为基学习器的GB算法。
注意：GBDT不论是用于分类还是回归，使用的决策树都是回归树。
GBDT中的决策树是弱模型，深度较小一般不会超过5，叶子节点的数量也不会超过10，对于每棵树乘上比较小的缩减系数shrinkage（学习率<0.1），有些GBDT的实现加入了随机抽样（subsample 0.5<=f <=0.8）提高模型的泛化能力。通过交叉验证的方法选择最优的参数。因此GBDT实际的核心问题变成怎么基于
和CART生成
。
再次强调GBDT使用的是回归树。回归树和分类树在分裂出新的分枝时是不同的。其对比见第0. CART节的表格1。
3. XGBoost
XGBoost算法的步骤与GBDT基本相同，不同之处主要有：
- GBDT只利用了一阶导数的信息，而XGBoost使用了一节倒数和二阶导数，迭代生成基学习器。XGBoost对损失函数进行二阶泰勒展开。
- XGBoost为损失函数添加正则项，以减少过拟合的风险
接下来，基于陈大神的PPT和论文来详细介绍XGBoost的损失函数，以及学习/训练过程，及公式的推倒过程。
3.1 XGBoost的学习过程
- XGBoost的损失函数:
|
|
公式（3.1） |
可以看到该损失函数由两部分组成，分别是：经验损失和正则项。其中，K代表分类器的个数，n代表样本的个数，f代表基分类器。
- XGBoost的学习过程：
由于是树结构模型，所以不能使用SGD等优化算法进行优化。其优化过程与Boosting一样，采用的是Additive Training（加法效应）：
注意：
虽然现在给出的是在每轮迭代中，直接向已有分类结果中添加新分类器的预测结果。但是实际上，XGBoost会为每轮的结果添加一个衰减权重
（就是learning rate）即：
，这可以使得每一棵树的影响力不会太大，留下更大的空间给后面生成的树去优化模型。
3.2 XGBoost推导
- 1. 定义损失函数
在第t次迭代的损失函数可以写成：
| 公式（3.2） |
由公式（3.2）可以看出，迭代过程是一个贪婪学习的过程，即添加最能够改进公式（3.2）的损失函数的
。
-
2. 利用泰勒公式进行变换
定义
分别为上一轮损失函数关于
的一阶倒数和二阶导数，
基于二阶泰勒展开公式:
，
将公式（3.2）进行变换，可以得到新的损失函数：
| 公式（3.3） |
- 3. 定义正则项，描述XGBoost的结构复杂度：
 |
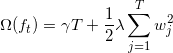公式（3.4） |
其中T代表叶子节点的数量，w代表叶子节点的权重。
-
4. 按照叶子节点的划分改写目标函数：
定义在叶子节点j中的样本集合为：
，q代表该叶子节点所在的树。
| |
公式（3.5） |
- 4. 对目标函数求解：
对于给定的树结构
，那么每个叶节点的最优权重w可以通过公式3.5求出，即：对所有
求导，并令其导数为0,即可求解。
 |
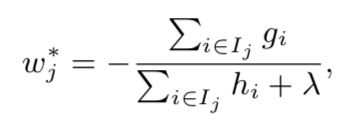公式（3.6） |
如此，损失函数可以被进一步改写为下面的公式。该公式可以用来度量树的结构的好坏。其中，L越小，说明结构越好。
 |
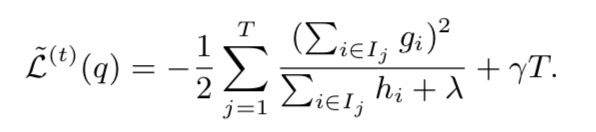公式（3.7） |
3.3 如何构建树结构 —— 分裂节点的算法？
与GBDT类似，XGBoost在划分的时候也不使用Gini系数作为衡量划分的好坏。
XGBoost采用的评估标准如下：
 |
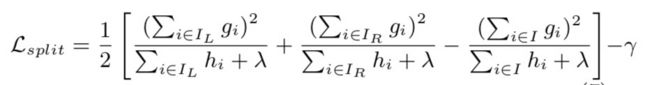公式（3.8） |
其中，
, 
代表划分到左右节点的样本集合。
3.3.1 Greedy Learning of the tree
算法1给出了利用贪婪算法来划分树的分枝。
注意：为了提高效率，在计算前会对样本在给定特征上按照值得大小进行排序。这样，在计算时就可以直接使用排序好的样本，进而提高计算速度。
3.2.2 Approximate Algorithm
对于连续型特征值，当样本数量非常大，该特征取值过多时，遍历所有取值会花费很多时间，且容易过拟合。因此XGBoost思想是对特征进行分桶，即找到l个划分点，将位于相邻分位点之间的样本分在一个桶中。在遍历该特征的时候，只需要遍历各个分位点，从而计算最优划分。
从算法伪代码中该流程还可以分为两种：
- 全局的近似是在新生成一棵树之前就对各个特征计算分位点并划分样本，之后在每次分裂过程中都采用近似划分
- 局部近似就是在具体的某一次分裂节点的过程中采用近似算法。
4. 针对稀疏数据的算法——缺失值处理
当样本的第i个特征值缺失时，无法利用该特征进行划分时，XGBoost的想法是将该样本分别划分到左结点和右结点，然后计算其增益，哪个大就划分到哪边。具体见算法3.
5. XGBoost减小过拟合的方式
- 在损失函数中添加正则项
- 在Additive Training中，在每次迭代的过程中，为新添加的函数指定一个缩减权重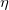，这可以使得每一棵树的影响力不会太大，留下更大的空间给后面生成的树去优化模型。即：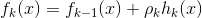
- Column Sampling: 类似于随机森林中的选取部分特征进行建树。其可分为两种，一种是按层随机采样，在对同一层内每个结点分裂之前，先随机选择一部分特征，然后只需要遍历这部分的特征，来确定最优的分割点。另一种是随机选择特征，则建树前随机选择一部分特征然后分裂就只遍历这些特征。一般情况下前者效果更好。
6. XGBoost的优点
- 使用许多策略去防止过拟合，如：正则化项、Shrinkage and Column Subsampling等。
- 目标函数优化利用了损失函数关于待求函数的二阶导数
- .支持并行化，这是XGBoost的闪光点，虽然树与树之间是串行关系，但是同层级节点可并行。具体的对于某个节点，节点内选择最佳分裂点，候选分裂点计算增益用多线程并行。训练速度快。
- 添加了对稀疏数据的处理。
- 交叉验证，early stop，当预测结果已经很好的时候可以提前停止建树，加快训练速度。
- 支持设置样本权重，该权重体现在一阶导数g和二阶导数h，通过调整权重可以去更加关注一些样本。
7. XGBoost vs. GBDT
- 传统的GBDT以CART树作为基学习器，XGBoost还支持线性分类器，这个时候XGBoost相当于L1和L2正则化的逻辑斯蒂回归（分类）或者线性回归（回归）；
- 传统的GBDT在优化的时候只用到一阶导数信息，XGBoost则对代价函数进行了二阶泰勒展开，得到一阶和二阶导数
- XGBoost在代价函数中加入了正则项，用于控制模型的复杂度。从权衡方差偏差来看，它降低了模型的方差，使学习出来的模型更加简单，放置过拟合，这也是XGBoost优于传统GBDT的一个特性；
- shrinkage（缩减），相当于学习速率（XGBoost中的eta）。XGBoost在进行完一次迭代时，会将叶子节点的权值乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。（GBDT也有学习速率）；
- Column Subsampling列抽样。XGBoost借鉴了随机森林的做法，支持列抽样，不仅防止过 拟合，还能减少计算；
- 对缺失值的处理。对于特征的值有缺失的样本，XGBoost还可以自动 学习出它的分裂方向；
- XGBoost工具支持并行。Boosting不是一种串行的结构吗?怎么并行 的？注意XGBoost的并行不是tree粒度的并行，XGBoost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。XGBoost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），XGBoost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代 中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。