PaddlePaddle | 深度学习 101- 线性回归

本人仅以 PaddlePaddle 深度学习 101 官网教程为指导，添加个人理解和笔记，仅作为学习练习使用，若有错误，还望批评指教。–ZJ

原文地址：PaddlePaddle 官网|PaddlePaddle 深度学习 101

环境：
- Python 2.7
- Ubuntu 16.04

先说个题外话，得先看官网文档中的环境支持的说明，不支持 windows 不支持 Python3 ,Ubuntu 中安装的时候，记得加 sudo ,好了，抽完自己两个大嘴巴子，（我这臭毛病，不要总是啥都不先了解下，看看文档的，就直接上手，太浪费时间）继续学吧。

线性回归

让我们从经典的线性回归（Linear Regression [1]）模型开始这份教程。在这一章里，你将使用真实的数据集建立起一个房价预测模型，并且了解到机器学习中的若干重要概念。

本教程源代码目录在book/fit_a_line， 初次使用请参考PaddlePaddle 安装教程，更多内容请参考本教程的视频课堂。

背景介绍

给定一个大小为n的数据集 {yi,xi1,…,xid}ni=1 { y i , x i 1 , … , x i d } i = 1 n ，其中 xi1,…,xid x i 1 , … , x i d 是第 i i 个样本 d d 个属性上的取值， yi y i 是该样本待预测的目标。线性回归模型假设目标 yi y i 可以被属性间的线性组合描述，即

yi=ω1xi1+ω2xi2+…+ωdxid+b,i=1,…,n y i = ω 1 x i 1 + ω 2 x i 2 + … + ω d x i d + b , i = 1 , … , n

例如，在我们将要建模的房价预测问题里， xij x i j 是描述房子i的各种属性（比如房间的个数、周围学校和医院的个数、交通状况等），而 yi y i 是房屋的价格。

初看起来，这个假设实在过于简单了，变量间的真实关系很难是线性的。但由于线性回归模型有形式简单和易于建模分析的优点，它在实际问题中得到了大量的应用。很多经典的统计学习、机器学习书籍2,3,4也选择对线性模型独立成章重点讲解。

效果展示

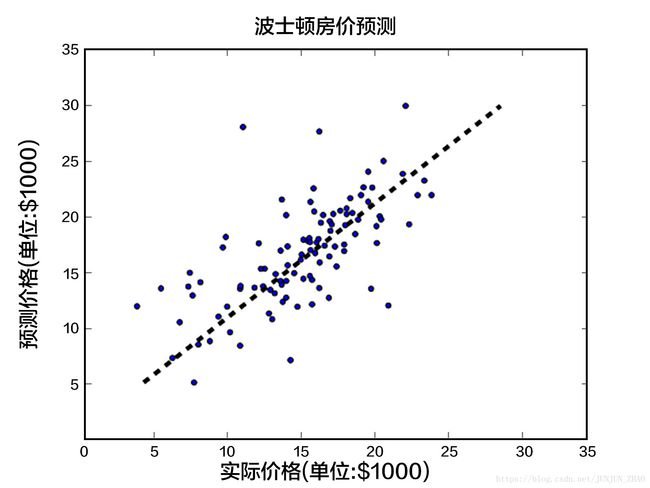
我们使用从UCI Housing Data Set获得的波士顿房价数据集进行模型的训练和预测。下面的散点图展示了使用模型对部分房屋价格进行的预测。其中，每个点的横坐标表示同一类房屋真实价格的中位数，纵坐标表示线性回归模型根据特征预测的结果，当二者值完全相等的时候就会落在虚线上。所以模型预测得越准确，则点离虚线越近。

图1. 预测值 V.S. 真实值

模型概览

模型定义

在波士顿房价数据集中，和房屋相关的值共有14个：前13个用来描述房屋相关的各种信息，即模型中的 xi x i ；最后一个值为我们要预测的该类房屋价格的中位数，即模型中的 yi y i 。因此，我们的模型就可以表示成：

Y^=ω1X1+ω2X2+…+ω13X13+b Y ^ = ω 1 X 1 + ω 2 X 2 + … + ω 13 X 13 + b

Y^ Y ^ 表示模型的预测结果，用来和真实值 Y Y 区分。模型要学习的参数即： ω1,…,ω13,b ω 1 , … , ω 13 , b 。

建立模型后，我们需要给模型一个优化目标，使得学到的参数能够让预测值 Y^ Y ^ 尽可能地接近真实值Y。这里我们引入损失函数（Loss Function，或 Cost Function）这个概念。 输入任意一个数据样本的目标值 yi y i 和模型给出的预测值 yi^ y i ^ ，损失函数输出一个非负的实值。这个实值通常用来反映模型误差的大小。

对于线性回归模型来讲，最常见的损失函数就是均方误差（Mean Squared Error， MSE）了，它的形式是：

MSE=1n∑i=1n(Yi^−Yi)2 M S E = 1 n ∑ i = 1 n ( Y i ^ − Y i ) 2

即对于一个大小为n的测试集， MSE M S E 是 n n 个数据预测结果误差平方的均值。

训练过程

定义好模型结构之后，我们要通过以下几个步骤进行模型训练

1. 初始化参数，其中包括权重 ωi ω i 和偏置 b b ，对其进行初始化（如 0 均值，1 方差）。
2. 网络正向传播计算网络输出和损失函数。
3. 根据损失函数进行反向误差传播 （backpropagation），将网络误差从输出层依次向前传递, 并更新网络中的参数。
4. 重复 2~3 步骤，直至网络训练误差达到规定的程度或训练轮次达到设定值。

数据集

数据集接口的封装

首先加载需要的包

#coding:utf-8
import os
import paddle.v2 as paddle
import paddle.v2.dataset.uci_housing as uci_housing

with_gpu = os.getenv('WITH_GPU', '0') != '0'

#print with_gpu
#print os.getenv('WITH_GPU', '0')
#print os.getenv('WITH_GPU', '1')

我们通过uci_housing模块引入了数据集合UCI Housing Data Set

其中，在 uci_housing 模块中封装了：

1. 数据下载的过程。下载数据保存在~/.cache/paddle/dataset/uci_housing/housing.data。
2. 数据预处理的过程。

数据集介绍

这份数据集共506行，每行包含了波士顿郊区的一类房屋的相关信息及该类房屋价格的中位数。其各维属性的意义如下：

属性名	解释	类型
CRIM	该镇的人均犯罪率	连续值
ZN	占地面积超过25,000平方呎的住宅用地比例	连续值
INDUS	非零售商业用地比例	连续值
CHAS	是否邻近 Charles River	离散值，1=邻近；0=不邻近
NOX	一氧化氮浓度	连续值
RM	每栋房屋的平均客房数	连续值
AGE	1940年之前建成的自用单位比例	连续值
DIS	到波士顿5个就业中心的加权距离	连续值
RAD	到径向公路的可达性指数	连续值
TAX	全值财产税率	连续值
PTRATIO	学生与教师的比例	连续值
B	1000(BK - 0.63)^2，其中BK为黑人占比	连续值
LSTAT	低收入人群占比	连续值
MEDV	同类房屋价格的中位数	连续值

数据预处理

连续值与离散值

观察一下数据，我们的第一个发现是：所有的13维属性中，有12维的连续值和1维的离散值（CHAS）。离散值虽然也常使用类似0、1、2这样的数字表示，但是其含义与连续值是不同的，因为这里的差值没有实际意义。例如，我们用0、1、2来分别表示红色、绿色和蓝色的话，我们并不能因此说“蓝色和红色”比“绿色和红色”的距离更远。所以通常对一个有 d d 个可能取值的离散属性，我们会将它们转为 d d 个取值为0或1的二值属性或者将每个可能取值映射为一个多维向量。不过就这里而言，因为CHAS本身就是一个二值属性，就省去了这个麻烦。

属性的归一化

另外一个稍加观察即可发现的事实是，各维属性的取值范围差别很大（如图2所示）。例如，属性B的取值范围是[0.32, 396.90]，而属性NOX的取值范围是[0.3850, 0.8170]。这里就要用到一个常见的操作-归一化（normalization）了。归一化的目标是把各位属性的取值范围放缩到差不多的区间，例如[-0.5,0.5]。这里我们使用一种很常见的操作方法：减掉均值，然后除以原取值范围。

做归一化（或 Feature scaling）至少有以下3个理由：
- 过大或过小的数值范围会导致计算时的浮点上溢或下溢。
- 不同的数值范围会导致不同属性对模型的重要性不同（至少在训练的初始阶段如此），而这个隐含的假设常常是不合理的。这会对优化的过程造成困难，使训练时间大大的加长。
- 很多的机器学习技巧/模型（例如L1，L2正则项，向量空间模型-Vector Space Model）都基于这样的假设：所有的属性取值都差不多是以0为均值且取值范围相近的。

(deep learning normalization [CN] P141 L1，L2正则项)

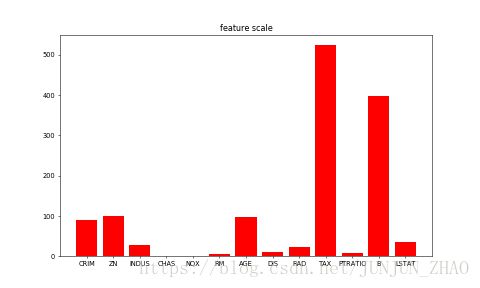
图2. 各维属性的取值范围

整理训练集与测试集

我们将数据集分割为两份：一份用于调整模型的参数，即进行模型的训练，模型在这份数据集上的误差被称为训练误差；另外一份被用来测试，模型在这份数据集上的误差被称为测试误差。我们训练模型的目的是为了通过从训练数据中找到规律来预测未知的新数据，所以测试误差是更能反映模型表现的指标。分割数据的比例要考虑到两个因素：更多的训练数据会降低参数估计的方差，从而得到更可信的模型；而更多的测试数据会降低测试误差的方差，从而得到更可信的测试误差。我们这个例子中设置的分割比例为 8:2 8 : 2

在更复杂的模型训练过程中，我们往往还会多使用一种数据集：验证集。因为复杂的模型中常常还有一些超参数（Hyperparameter）需要调节，所以我们会尝试多种超参数的组合来分别训练多个模型，然后对比它们在验证集上的表现选择相对最好的一组超参数，最后才使用这组参数下训练的模型在测试集上评估测试误差。由于本章训练的模型比较简单，我们暂且忽略掉这个过程。

训练

fit_a_line/trainer.py演示了训练的整体过程。

初始化PaddlePaddle

paddle.init(use_gpu=False, trainer_count=1)

模型配置

线性回归的模型其实就是一个采用线性激活函数（linear activation，LinearActivation）的全连接层（fully-connected layer，fc_layer）：

# network config
# 定义训练数据 x 根据上述文章描述，前 13 个属性或特征作为 一个样本的训练数据
x = paddle.layer.data(name='x', type=paddle.data_type.dense_vector(13))
# 激活函数 使用 Linear() 线性回归 对 y_predict 进行预测
y_predict = paddle.layer.fc(input=x,
                                size=1,
                                act=paddle.activation.Linear())
# 定义 1 个值作为真实数据的 标签 y
y = paddle.layer.data(name='y', type=paddle.data_type.dense_vector(1))
# 使用均方根误差 计算 真实值 y 和预测值 y_predict 之间的损失函数
cost = paddle.layer.square_error_cost(input=y_predict, label=y)

保存网络拓扑

# Save the inference topology to protobuf.
inference_topology = paddle.topology.Topology(layers=y_predict)
with open("inference_topology.pkl", 'wb') as f:
    inference_topology.serialize_for_inference(f)

创建参数

parameters = paddle.parameters.create(cost)

创建Trainer

# create optimizer 优化函数 使用 Momentum 函数
optimizer = paddle.optimizer.Momentum(momentum=0)
# SGD 随机梯度下降
trainer = paddle.trainer.SGD(cost=cost,
                             parameters=parameters,
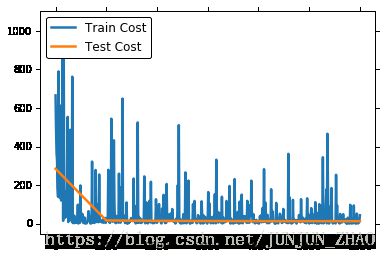
                             update_equation=optimizer)

读取数据且打印训练的中间信息

PaddlePaddle提供一个
reader机制
来读取数据。 Reader返回的数据可以包括多列，我们需要一个Python dict把列
序号映射到网络里的数据层。

feeding={'x': 0, 'y': 1}

此外，我们还可以提供一个 event handler，来打印训练的进度：

# event_handler to print training and testing info
def event_handler(event):
    if isinstance(event, paddle.event.EndIteration):
        if event.batch_id % 100 == 0:
            print "Pass %d, Batch %d, Cost %f" % (
                event.pass_id, event.batch_id, event.cost)

    if isinstance(event, paddle.event.EndPass):
        result = trainer.test(
            reader=paddle.batch(
                uci_housing.test(), batch_size=2),
            feeding=feeding)
        print "Test %d, Cost %f" % (event.pass_id, result.cost)

# event_handler to print training and testing info
from paddle.v2.plot import Ploter

train_title = "Train cost"
test_title = "Test cost"
cost_ploter = Ploter(train_title, test_title)

step = 0

def event_handler_plot(event):
    global step
    if isinstance(event, paddle.event.EndIteration):
        if step % 10 == 0:  # every 10 batches, record a train cost
            cost_ploter.append(train_title, step, event.cost)

        if step % 100 == 0: # every 100 batches, record a test cost
            result = trainer.test(
                reader=paddle.batch(
                    uci_housing.test(), batch_size=2),
                feeding=feeding)
            cost_ploter.append(test_title, step, result.cost)

        if step % 100 == 0: # every 100 batches, update cost plot
            cost_ploter.plot()

        step += 1

    if isinstance(event, paddle.event.EndPass):
        if event.pass_id % 10 == 0:
            with open('params_pass_%d.tar' % event.pass_id, 'w') as f:
                trainer.save_parameter_to_tar(f)

开始训练

trainer.train(
    reader=paddle.batch(
        paddle.reader.shuffle(
            uci_housing.train(), buf_size=500),
        batch_size=2),
    feeding=feeding,
    event_handler=event_handler_plot,
    num_passes=30)

应用模型

1. 生成测试数据

test_data_creator = paddle.dataset.uci_housing.test()
test_data = []
test_label = []

for item in test_data_creator():
    test_data.append((item[0],))
    test_label.append(item[1])
    if len(test_data) == 5:
        break

2. 推测 inference

# load parameters from tar file.
# users can remove the comments and change the model name
# with open('params_pass_20.tar', 'r') as f:
# parameters = paddle.parameters.Parameters.from_tar(f)

probs = paddle.infer(
    output_layer=y_predict, parameters=parameters, input=test_data)

for i in xrange(len(probs)):
    print "label=" + str(test_label[i][0]) + ", predict=" + str(probs[i][0])

Pass 0, Batch 0, Cost 504.985291
Pass 0, Batch 100, Cost 76.352913
Pass 0, Batch 200, Cost 19.661787
Test 0, Cost 57.820578
Pass 1, Batch 0, Cost 50.965809
Pass 1, Batch 100, Cost 502.039764
Pass 1, Batch 200, Cost 6.086728
Test 1, Cost 22.656893
Pass 2, Batch 0, Cost 54.926193
Pass 2, Batch 100, Cost 228.025314
Pass 2, Batch 200, Cost 156.193985
Test 2, Cost 18.244162
.
.
.
Pass 27, Batch 0, Cost 62.841465
Pass 27, Batch 100, Cost 22.502949
Pass 27, Batch 200, Cost 9.409659
Test 27, Cost 13.181028
Pass 28, Batch 0, Cost 42.877792
Pass 28, Batch 100, Cost 175.905655
Pass 28, Batch 200, Cost 16.661724
Test 28, Cost 13.134191
Pass 29, Batch 0, Cost 5.657633
Pass 29, Batch 100, Cost 28.668287
Pass 29, Batch 200, Cost 5.999536
Test 29, Cost 13.223995
label=8.5, predict= 11.762322
label=5.0, predict= 13.696922
label=11.9, predict= 10.7507
label=27.9, predict= 18.100128
label=17.2, predict= 13.044429

总结

在这章里，我们借助波士顿房价这一数据集，介绍了线性回归模型的基本概念，以及如何使用PaddlePaddle实现训练和测试的过程。很多的模型和技巧都是从简单的线性回归模型演化而来，因此弄清楚线性模型的原理和局限非常重要。

参考文献

1. https://en.wikipedia.org/wiki/Linear_regression
2. Friedman J, Hastie T, Tibshirani R. The elements of statistical learning[M]. Springer, Berlin: Springer series in statistics, 2001.
3. Murphy K P. Machine learning: a probabilistic perspective[M]. MIT press, 2012.
4. Bishop C M. Pattern recognition[J]. Machine Learning, 2006, 128.