空间索引-四叉树的实现及其应用

什么是四叉树？

四叉树（Quad Tree）是一种空间索引树，四叉树的每一个节点都代表着一块矩形区域。我们知道在平面直角坐标系中，平面可以被分为第一二三四象限，四叉树的每一个节点也类似，可以分裂为四个子节点，子节点在满足条件的情况下可以继续分裂，这样构成了一个四元的树状结构，就是四叉树。

 

四叉树的作用

通常使用树结构能够带来高效且简单的检索效果，四叉树也不例外，四叉树主要用于二维空间的检索（相应的，三维空间可以了解下八叉树，理论上来讲，对于N维空间的检索可以根据这个原理构成2^N叉树，此外多维空间的检索还有kd树）。

下面是用四叉树来存储某平面区域上许多小矩形的例子

其中这个区域被分为了许多个小矩形，每一个矩形都代表了一个四叉树的一个节点，最外层的大矩形就是四叉树的根节点（root），一些矩形被分割成了四个等大的小矩形，这是该节点的四个子节点，矩形越小，说明该节点的深度（depth）越大

四叉树的高效检索

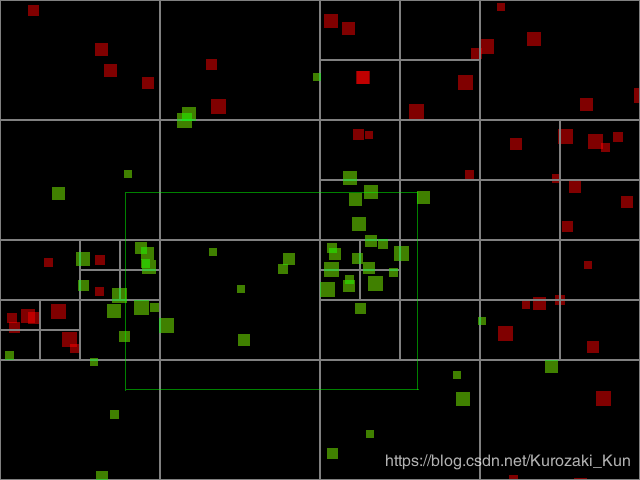
下面是检索四叉树的某一矩形区域的例子

其中，与绿框无相交区域的节点不会被检索，这样一来可以大大减少检索量

（为什么有一些在绿框外的节点也会被检索到？这根存储方式有关，上面的实现是将落在分割线上的矩形存储在了父节点，这样只要检索区域与节点有相交，就要返回节点内所有的元素）

四叉树的操作

1、节点分裂

当满足特定条件时，为了获得更好的检索效率，四叉树的节点会发生分裂，分裂的做法是：以当前节点的矩形为中心， 划分出四个等大的矩形，作为四个子节点，每个节点深度=当前节点深度+1，根节点深度为0；并且将当前节点的元素重新插入到对应的子节点。

2、插入元素

1）平面的元素多种多样，点，线，图形，但都能够做一个统一，第一步都是要找出图形所覆盖的节点，这里以矩形为例

2）从根节点开始，如果当前节点无子节点，将元素插入到当前节点。如果存在子节点K，并且元素能够完全被子节K点所“包围”，就将元素插入到子节点K，对于子节点K进行上述递归操作；如果元素跨越了多个子节点，那就将元素存储在当前节点

3）如果某一节点元素超过特定值，并且深度小于四叉树允许的最大深度，分裂当前节点。

3、检索

1）对于给定检索区域，从根节点起，如果检索区域与当前节点有交集，返回当前节点的所有元素。

2）如果当前节点还有子节点，递归检索与检索区域有交集的子节点。

 

代码实现（Java）

public class QuadTree {

    private Node root;

    public NormalQuadTree(Rectangle boundary) {
        this.root = new Node<>(boundary, 0);
    }

    public boolean insert(T t) {
        return root.insert(t);
    }

    public Set retrieve(Rectangle retArea) {

        return root.retrieve(retArea);
    }

    private static class Node {

        static final int MAX_OBJECT_COUNT = 5;
        static final int MAX_DEEP = 4;

        static final int LEFT_TOP = 0;
        static final int LEFT_BOTTOM = 1;
        static final int RIGHT_TOP = 2;
        static final int RIGHT_BOTTOM = 3;

        private Rectangle boundary;
        private Set objectSet;

        private List> childs = new ArrayList<>(4);

        private final int deep;

        Node(Rectangle boundary, int deep) {
            this.boundary = boundary;
            this.deep = deep;
            this.objectSet = new HashSet<>();
        }

        boolean insert(T t) {
            if (!t.intersects(this.boundary)) {
                return false;
            }

            if (!childs.isEmpty()) {
                int quadIndex = quadrantOf(t);
                if (quadIndex != -1) {
                    return childs.get(quadIndex).insert(t);
                }
            }

            this.objectSet.add(t);
            if (this.childs.isEmpty()
                    && this.objectSet.size() > MAX_OBJECT_COUNT
                    && this.deep < MAX_DEEP) {
                this.split();
            }
            return true;
        }

        void split() {
            int hmid = this.boundary.x + this.boundary.width / 2;
            int vmid = this.boundary.y + this.boundary.height / 2;

            this.childs.add(LEFT_TOP, new Node<>(new Rectangle(
                    boundary.x,
                    boundary.y,
                    boundary.width / 2,
                    boundary.height / 2
            ), deep + 1));

            this.childs.add(LEFT_BOTTOM, new Node<>(new Rectangle(
                    boundary.x,
                    vmid,
                    boundary.width / 2,
                    boundary.height / 2
            ), deep + 1));

            this.childs.add(RIGHT_TOP, new Node<>(new Rectangle(
                    hmid,
                    boundary.y,
                    boundary.width / 2,
                    boundary.height / 2
            ), deep + 1));

            this.childs.add(RIGHT_BOTTOM, new Node<>(new Rectangle(
                    hmid,
                    vmid,
                    boundary.width / 2,
                    boundary.height / 2
            ), deep + 1));

            Set temp = this.objectSet;
            this.objectSet = new HashSet<>();
            for (T t : temp) {
                insert(t);
            }
        }

        int quadrantOf(Rectangle rect) {
            int hmid = this.boundary.x + this.boundary.width / 2;
            int vmid = this.boundary.y + this.boundary.height / 2;

            int index = -1;
            if (rect.x + rect.width < hmid && rect.y + rect.height < vmid) {
                index = LEFT_TOP;
            } else if (rect.x + rect.width < hmid && rect.y > vmid) {
                index = LEFT_BOTTOM;
            } else if (rect.x > hmid && rect.y + rect.height < vmid) {
                index = RIGHT_TOP;
            } else if (rect.x > hmid && rect.y > vmid) {
                index = RIGHT_BOTTOM;
            }
            return index;
        }

        Set retrieve(Rectangle retArea) {
            if (retArea.isEmpty()) {
                return new HashSet<>();
            }

            Set resultSet = new HashSet<>(objectSet);

            if (!childs.isEmpty()) {
                int index = quadrantOf(retArea);
                if (index != -1) {
                    return childs.get(index).retrieve(retArea);
                }
                for (Node node : childs) {
                    Rectangle inter = node.boundary.intersection(retArea);
                    if (!inter.isEmpty()) {
                        resultSet.addAll(node.retrieve(inter));
                    }
                }
            }
            return resultSet;
        }
    }
}

四叉树的应用

游戏开发中经常有碰撞检测的算法，对于平面上N个图形，如果需要检测互相之间是否发生碰撞，最基本的做法是进行N(N-1)次比较，时间复杂度是O(n^2)，n较小时能够接受，当n>10000时效率可能就会明显降低了，如果四叉树使用合理，可以将复杂度降到O(nlog n)，可以说是个很大的改进。

 

四叉树的优化

1、有人会发现这个四叉树没有删除算法，因为游戏开发中遇到的平面图形常常是频繁移动的（都静态的话就用不着相互之间碰撞检测了），这就意味着每一帧都要重建四叉树，这样就自然地避免了删除特定节点。但是也应该能想到大致优化的方案了吧，只修改移动后所在覆盖节点发生变化的元素，将其删除再插入。四叉树如果要实现删除首先也得检索删除元素所在节点，删除结束后，考虑到空间占用，可能要进行子节点的合并。

2、来看下面这棵四叉树

由于元素分布均匀，导致四叉树变成了一个看起来近似网格的结构

在一维元素中，满二叉树可以用一维数组存储

类似的，四叉树在元素均匀分布的条件下可以用二维数组存储

这样做的好处是

1）检索更快

检索四叉树的某个元素所在的节点需要O(log n)的复杂度，而二维数组只需要O(1)，很简单，就是计算一下所坐标，转换成二维数组的下标

2）维护更加简便

二维数组的方式避免了递归操作