机器学习（周志华）课后作业/习题答案

前言：本系列作业系笔者个人主观完成，一家之言因此难免有不当之处，仅供参考。此外笔者只完成部分认为有用的问题。

李航《统计学习方法》答案见：统计学习方法

持续更新中…

第一章

1.1

通常情况下，版本空间是正例的泛化。在我们确定学习目标之后（比如找到“好瓜”，视为正例），可能有多个假设（hypothesis）是跟我们的目标一致的，满足训练集。也就是说可能有多种假设满足我们“好瓜”的要求。因此版本空间就是所有满足这个正例的结果的集合。因而我们的方法是：先把假设空间（hypothesis space）找出来，然后踢出与正例不一致的假设。或者直接找出能够实现正例的hypothesis，我打算用后者。
假如只有编号1和4两个样例，则考虑通配符*和空集$\varphi$. 所以hypothesis space的规模为：$3\times 3\times 3+1=28$。
对着第四页的表1.1，能够实现正例的hypothesis（即能够找到好瓜的）有：

• {青绿 蜷缩 浊响}
  上面是限制最强的，即最没有泛化的情况，在这种情况下慢慢往外推，有：
  一个通配符的：
• {* 蜷缩 浊响}
• {青绿 * 浊响}
• {青绿 蜷缩 *}
  两个通配符的
• {* * 浊响}
• {* 蜷缩 *}
• {青绿 * *}
  因此有7中情况

第二章

2.1

这是一个排列组合问题。有1000个样本，500个正例，500个反例。那么我们先考虑训练集，因为训练集一旦定了，那么剩下的样本就都放测试集，也就是测试集也定了。
在留出法中，要保持测试集和训练集的类别比列相似，也就是分层采样。因此训练集需要350个正例，350个反例。即
$$C_{500}^{350}\times C_{500}^{350}$$

2.2

数据包含100个样例，使用10折交叉验证，则依据分层采样。分成十份，每份有5个正例5个反例。则训练集是十份中的9份，每份的正反例是一样的，此时依照题目随机猜，因此错误率为50%。
当使用留一法：表示将100个样例分成100份。假设测试集是一个正例，那么训练集中有50个反例和一个正例，那么学习算法学得的模型将会把测试集判断为反例，判断错误。留下的是反例亦然。错误率100%。

2.3

对这个题始终还有疑问，即这个题是否提问得恰当？
P-R曲线的由来如P31页所述。是对样例先进行排序，拍在前面是最可能正例的样本，后面是最不可能正例的样本，然后按顺序逐个把正例进行预测，每次预测都可以计算出当前的查全率和查准率（亦即每次都可以有F1），并画出P-R图。如此到题中，若学习器A的F1值比学习器B高。说的是某次计算中A的F1大于B的F1，（并不是所有的次数A都大于B，因为实际实验只做一次），此时题目问的却是A的BEP值是否比B高。这个值显然是不知道的。因为BEP值要求P=R，而F1的定义是
$$\frac{1}{F1}=\frac{1}{2}\times \left(\frac{1}{P}+\frac{1}{R}\right)$$
注意此时的P和R不是相等的。因此结果是未知的。

第三章

课文整理/代码实现部分

此部分目的在于通过现有程序来实现线性模型对测试集的预估。
求解过程中使用的梯度下降算法可以见：梯度下降法
第三章主要讲了线性模型，基本形式为：
$$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b$$详细过程会在代码中解释清楚。

# import packages that may be used
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn import datasets
from sklearn.metrics import mean_squared_error,r2_score

#make data linear regression from datasets
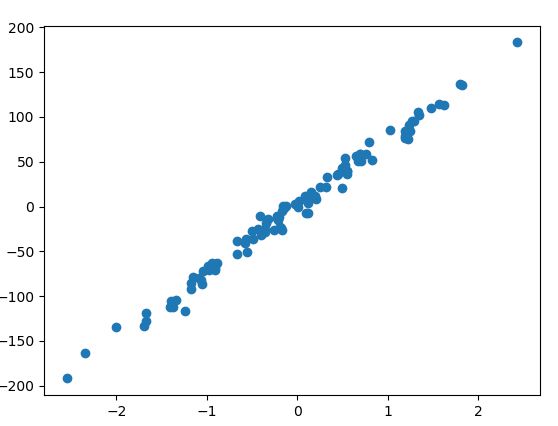
X,Y = datasets.make_regression(n_samples=100, n_features=1, n_targets=1, noise=8)
plt.scatter(X,Y)
plt.show()

#split the data into training/testing sets
X_train = X[:-30]
X_test = X[-30:]

#split the targets into training/testing sets
Y_train = Y[:-30]
Y_test = Y[-30:]

#create linear regression object
reg = linear_model.LinearRegression()

#Train the model using the training sets
reg.fit(X_train,Y_train)

#Make predictions using the testing set
test_pred = reg.predict(X_test)

# The coefficients 
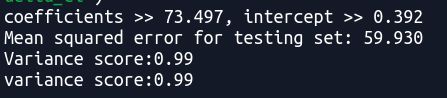
print('coefficients >> %.3f, intercept >> %.3f '%(reg.coef_, reg.intercept_))

# The mean sqwared error
print('Mean squared error for testing set: %.3f' %mean_squared_error(Y_test,test_pred))

# Explained variance score: 1 is perfect prediction
print('Variance score:%.2f'%r2_score(Y_test,test_pred))
print("variance score:%.2f" % reg.score(X_test, Y_test))

说明：

1）R2_score等于1是最好的结果（可看线性模型的链接内容，sklearn.linear_model.LinearRegression）
2）上面使用的实例只有一个feature/attribute, 从结果来看，线性方程形式为：
$$f(x)=73.497x+0.392$$
比如我再预测一个当x=3时的f(x)值

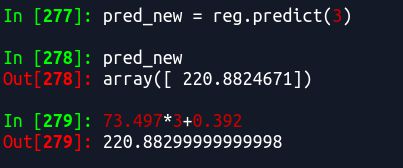
结果是一样的（小数点后不同是因为我上面输出保留的是3位小数）
对于线性模型可以看这个链接sklearn.linear_model.LinearRegression
例子可以看linearRegression example

以上数据是datasets生成的，对于自己使用的数据可以如下：

# import packages that may be used
import numpy as np
from sklearn import linear_model

#make data linear regression from datasets
x1 = [0,1,2.2,3,3.4,5,8,10,13,15]
x2 = [2,3,4,5,2,3,4,5,18,23]

X = np.array([[0,2],[1,3],[2.2,4],[3,5],[3.4,2],[5,3],[6,4],[10,5],[13,18],[15,23]])

# y = 2+3*x1+7*x2
Y = 2+np.dot(X,np.array([3,2]))

#create linear regression object
reg = linear_model.LinearRegression()

#Train the model using the training sets
reg.fit(X,Y)

#Make predictions using the testing set
test_pred = reg.predict(np.array([[4,2]]))

# The coefficients 
print('coefficients and intercept >> ',(reg.coef_, reg.intercept_))

3.1

偏置项对于研究$f(x)$与$x$之间的关系没有影响，只相当于坐标系从坐标原点移动了$b$距离。如
$f(x)=ax+b$中$x$与$f(x)$是一次关系，斜率为$a$,$b$只是相当于坐标系从原点上移了$b$距离。因此在研究$f(x)$与$x$之间的关系时，$b$无关紧要。数学上，既然是移动了坐标系，也可以通过将坐标系移动回到原点即可消除$b$的影响。通过将所有数据减去数据中的同一个数据可以达到效果，即
$$f({\mathbf{x}}_i-x_0)={\mathbf{w}}^T({\mathbf{x}}_i-x_0)$$
举例如下：

# import packages that may be used
import numpy as np
from sklearn import linear_model

#make data linear regression from datasets
x1 = [0,1,2.2,3,3.4,5,8,10,13,15]
x2 = [2,3,4,5,2,3,4,5,18,23]

X = np.array([[0,2],[1,3],[2.2,4],[3,5],[3.4,2],[5,3],[6,4],[10,5],[13,18],[15,23]])

# y = 2+3*x1+7*x2
Y = 2+np.dot(X,np.array([3,7]))

#new data
X = X-X[0]
Y = Y-Y[0]
#create linear regression object
reg = linear_model.LinearRegression()

#Train the model using the training sets
reg.fit(X,Y)

#Make predictions using the testing set
test_pred = reg.predict(np.array([[4,2]]))
print('prediction_test',test_pred)

# The coefficients 
print('coefficients and intercept >> ',(reg.coef_, reg.intercept_))

可见偏置项约定于0

3.2

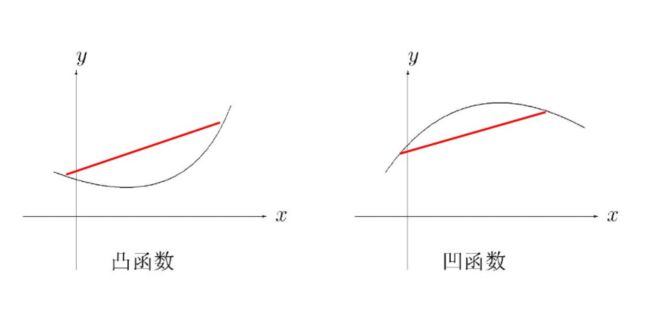
首先给出凸函数(convex function)的定义和性质

顺便一提，也有凹函数的定义（凸函数和凸优化）：



note:

1. 严格凸函数：二阶导数在区间上恒大于0
2. U形曲线函数如$y=x^2$通常是凸函数

性质：
凸函数的局部最优解是全局最优解，任何极小值也是全局最小值。严格凸函数最多有一个最小值，即最优解唯一。
凸函数的证明方法

• 通过定义式
• 对于连续凸函数，通过求两阶导，如果两阶导在区间上非负，则是凸函数

参考文献：

1 关于凸函数的定义和性质
2 凸函数和凸优化

3.3

2. 通过导入包的方法

先对数据scatter出来，有一个整体印象

# import packages that may be used
import numpy as np
import matplotlib.pyplot as plt

#make data linear regression from datasets
dataset = np.loadtxt(r'/media/sf_Share/Machine learning/zhouzhihua_solutions/3/watermelon_3.0a.txt')

# plot data
X = dataset[:,1:3]
Y = dataset[:,3]
plt.scatter(X[Y == 0,0], X[Y == 0,1], marker = 'o', color = 'k', s=30, label = 'NO')   #scatter the data where Y=0
plt.scatter(X[Y == 1,0], X[Y == 1,1], marker = 'o', color = 'g', s=30, label = 'YES')  #scatter the data where Y=1
plt.legend(loc = 'upper right')  

plt.show()

从sklearn导入包，并将数据部分作为训练部分作为预测

# import packages that may be used
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score

#make data linear regression from datasets
dataset = np.loadtxt(r'/media/sf_Share/Machine learning/zhouzhihua_solutions/3/watermelon_3.0a.txt')

#split dataset to training/testing sets
train_data, test_data = train_test_split(dataset,test_size=0.3, random_state=0)
X_train = train_data[:,1:3]
Y_train = train_data[:,3]
X_test = test_data[:,1:3]
Y_test = test_data[:,3]

#create logistic regression object
reg = linear_model.LogisticRegression()

#Train the model using the training sets
reg.fit(X_train,Y_train)

#Make predictions using the testing set
test_pred = reg.predict(X_test)
print('prediction_test',test_pred)

# The coefficients 
coeffs = reg.coef_
b = reg.intercept_
print('coefficients and intercept >> ',(reg.coef_, reg.intercept_))

# The mean sqwared error
print('Mean squared error for testing set: %.3f' %mean_squared_error(Y_test,test_pred))

# Explained variance score: 1 is perfect prediction
print('Variance score:%.2f'%r2_score(Y_test,test_pred))
print("variance score:%.2f" % reg.score(X_test, Y_test))

需要的数据如下：
总的数据

训练数据为：

测试数据为：

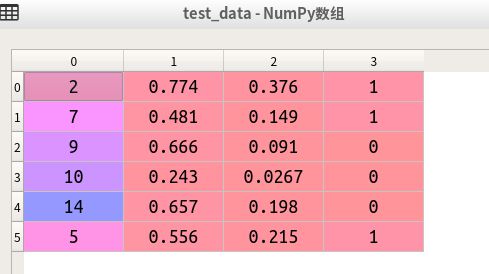
最后给出的结果

从结果来看，测试很差，给出的预测都是0（即不是好瓜），而真实数据有三个好瓜，三个不是好瓜。

note:

• train_data, test_data = train_test_split(dataset,test_size=0.3, random_state=0)这里可以将test_size=0.3改为=3，表示有3个用于测试