周志华《机器学习》课后习题解答系列（四）：Ch3.5 - 编程实现线性判别分析

本系列主要采用Python-sklearn实现，环境搭建可参考 数据挖掘入门：Python开发环境搭建（eclipse-pydev模式）.

相关答案和源代码托管在我的Github上：PnYuan/Machine-Learning_ZhouZhihua.

3.5 编程实现线性判别分析（LDA）

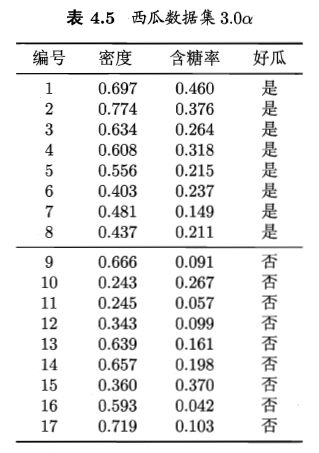
本题采用题3.3中的西瓜数据集如下图示：

这里采用基于sklearn和自己编程实现两种方式实现线性判别分析（查看完整代码）。

关于数据集的介绍：

具体过程如下：

1. 数据导入、可视化、预分析：

可以参照周志华《机器学习》课后习题解答系列（四）：Ch3.3 - 编程实现对率回归中的第一步。

2. 采用sklean得到线性判别分析模型：

采用sklearn.discriminant_analysis.LinearDiscriminantAnalysis直接实现基础的LDA，通过分割数据集，在训练集上训练数据，在预测集上度量模型优劣。

给出样例代码如下：

from sklearn import model_selection
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import metrics
import matplotlib.pyplot as plt

# generalization of train and test set
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.5, random_state=0)

# model fitting
lda_model = LinearDiscriminantAnalysis(solver='lsqr', shrinkage=None).fit(X_train, y_train)

# model validation
y_pred = lda_model.predict(X_test)

# summarize the fit of the model
print(metrics.confusion_matrix(y_test, y_pred))
print(metrics.classification_report(y_test, y_pred))

得出的混淆矩阵及相关度量结果如下：

[[4 1]
 [1 3]]
             precision    recall  f1-score   support

        0.0       0.80      0.80      0.80         5
        1.0       0.75      0.75      0.75         4

avg / total       0.78      0.78      0.78         9

可以看出，由于数据集的散度不太明显，得出的类别判断存在较大误差。总体来看，这里的线性判别分类器与3.3题的对率回归性能相当（accuracy≈0.78）。

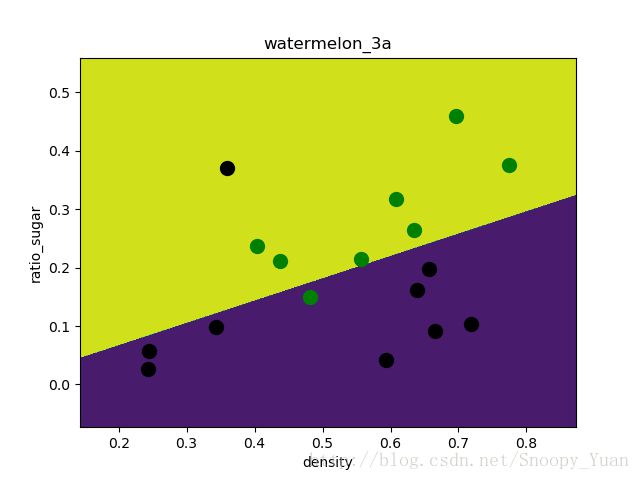
基于matplotlib绘制出LDA的分类区域如下图示：

可以看出，LDA的决策区域与3.3采用对率回归得到的结果相当。

3. 自己编程实现线性判别分析：

关于LDA的原理及参数求解，可参考书上p61、62。所谓线性判别。类似PCA，LDA可将较高维数据投影到较低维空间上，分析其降维后的数据特征的类别区分情况。

这里采用西瓜数据集，包含2个属性（特征），一个类标签（二分类0、1）。在此上运用LDA，即是要找到最优直线，映射到直线上的数据特征类分明显。

如何区分类别呢？采用类内散度（within-class scatter）最小化，类间散度（between-class scatter）最大化，关于散度的定义参考书中p61式(3.33)和(3.34)。

优化目标为最大化下式（Sw-类内散度，Sb-类间散度，w-直线方向向量）：

我们的目的是最大化上面的式子，根据书中推导，最优解（直线参数）如下式：

相关详细过程参考树p61-62页。

• 编程：根据式3.39计算w：

样例代码如下：

# computing the d-dimensional mean vectors
import numpy as np

# 1-st. get the mean vector of each class
u = []  
for i in range(2): # two class
    u.append(np.mean(X[y==i], axis=0))  # column mean

# 2-nd. computing the within-class scatter matrix, refer on book (3.33)
m,n = np.shape(X)
Sw = np.zeros((n,n))
for i in range(m):
    x_tmp = X[i].reshape(n,1)  # row -> cloumn vector
    if y[i] == 0: u_tmp = u[0].reshape(n,1)
    if y[i] == 1: u_tmp = u[1].reshape(n,1)
    Sw += np.dot( x_tmp - u_tmp, (x_tmp - u_tmp).T )

# 3-th. computing the parameter w, refer on book (3.39)
# here we use singular value decomposition(SVD) to get the inverse of a ndarray
Sw = np.mat(Sw)
U, sigma, V= np.linalg.svd(Sw) 
Sw_inv = V.T * np.linalg.inv(np.diag(sigma)) * U.T

w = np.dot( Sw_inv, (u[0] - u[1]).reshape(n,1) )  
print(w)

• 绘制LDA直线并作数据点投影来查看类簇情况：

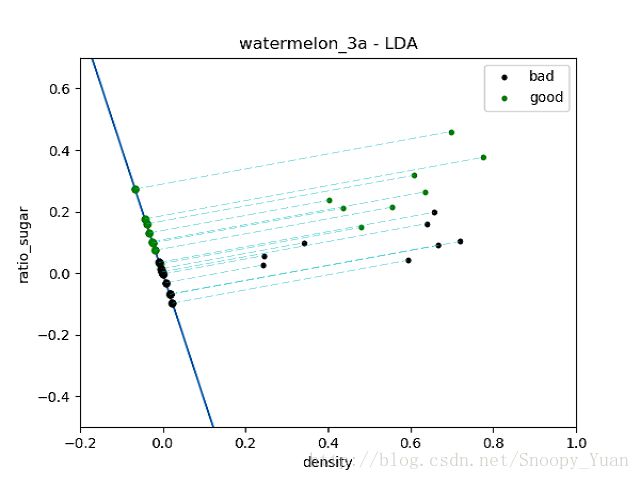
通过绘制投影的方式，可视化西瓜数据在LDA直线上类簇情况（查看相关代码），如下图示：

从上图看出，由于数据线性不可分，则出现类簇重叠现象。接下来，通过观查数据，我们考虑将西瓜数据集中的bad类离群点15删去（即图中左上的黑点）此时数据集的线性可分性大大提高。

然后再次采用LDA进行映射，得到结果图如下：

可以看出，在数据集变得线性可分时，二维点到一维LDA直线的投影出现明显的分类，此时LDA分类器效果很好。

综上所述，由于西瓜数据集自身非线性因素，LDA所得直线未能很好的表现出类别的分簇情景，说明，LDA基本模型不太适用于线性不可分的情况。要拓展到非线性，或许可以考虑SVM-核技巧。

本文的一些重要索引如下：

• Linear Discriminant Analysis - 关于LDA的详细介绍和本质剖析
• sklearn官网 - LDA for classfication