《机器学习》周志华西瓜书习题参考答案：第4章 - 决策树

【机器学习】《机器学习》周志华西瓜书 笔记/习题答案 总目录

• https://blog.csdn.net/TeFuirnever/article/details/96178919

——————————————————————————————————————————————————————

• 【机器学习】《机器学习》周志华西瓜书读书笔记：第4章 - 决策树
• 【机器学习】《机器学习实战》读书笔记及代码：第3章 - 决策树

习题

从原书p74的图4.2的决策树学习的基本算法可以看出，生成一个叶节点有三种情况：

1.节点下样本 $D$ 全属于同一类样本 $C$ ，则将当前节点作为 $C$ 类叶节点。

2.属性集 ，或者样本在当前属性集上取值相同。即特征用完了（当只剩最后一个特征时，进一步分裂，只能将各取值设立叶节点，标记为样本最多的类别。），或者样本在 $A$ 上取值都相同（感觉这里貌似和第 一条重复了）。这时取 $D$ 中最多的类作为此节点的类别标记。

3.在某一节点上的属性值 $a_{\ast }^v$ ，样本为空，即没有样本在属性 $a_{\ast }$ 上取值为 $a_{\ast }^v$ 。同样取 $D$ 中最多的类作为此节点的类别标记。

在这道题中，目标是找出和训练集一致的决策树，所以不必考虑第3点，从1、2情况来看出决策树中树枝停止“生长”生成叶节点只会在样本属于同一类或者所有特征值都用完的时候，那么可能导致叶节点标记与实际训练集不同时只会发生在特征值都用完的情况（同一节点中的样本，其路径上的特征值都是完全相同的），而由于训练集中没有冲突数据，那每个节点上训练误差都为0，必存在与训练集一致（训练误差为0）的决策树。

若以最小训练误差作为决策树划分的依据，由于训练集和真是情况总是会存在一定偏差，这使得这样得到的决策树会存在过拟合的情况，对于未知的数据的泛化能力较差。

因为数据集的原因，数据量比较小，在选择划分属性的时候会出现特征的信息增益或者信息增益率相同的情况。所有生成的决策树和书中可能不一致，并且在生成叶节点时，会出现两类数量一直的情况，这时候叶节点就随机设置一个分类了。

代码实现了以信息增益、增益率、基尼指数划分准则。下面一道题（4.4）也是用相同的代码。另外画图的代码是主要参考《机器学习实战》决策树那一章画图源码。【机器学习】《机器学习实战》读书笔记及代码：第3章 - 决策树

代码在：https://github.com/han1057578619/MachineLearning_Zhouzhihua_ProblemSets/tree/master/ch4–%E5%86%B3%E7%AD%96%E6%A0%91/4.3-4.4

生成决策树如下：

总体来说后剪枝会相比于预剪枝保留更多的分支。有两个需要注意的地方。一个是在4.3中说过的，因为划分属性的信息增益或者基尼指数相同的原因，这个时候选择哪一个属性作为划分属性都是对的，生成决策树和书中不一致是正常的（书中第一个节点为“脐部”）。另外数据量这么小的情况下，常常会出现剪枝前后准确率不变的情况，原书中也提到这种情况通常要进行剪枝的，但是这道题中若进行剪枝，会出现只有一个叶节点的情况。为了画图好看点…所以无论在预剪枝还是后剪枝中，这种情况都会采取不剪枝策略。参考原书P82。

经过测试，在未剪枝的情况下，验证集上准确率为0.2857；后剪枝准确率为0.5714；预剪枝也为0.5714。

代码在：https://github.com/han1057578619/MachineLearning_Zhouzhihua_ProblemSets/tree/master/ch4–%E5%86%B3%E7%AD%96%E6%A0%91/4.3-4.4

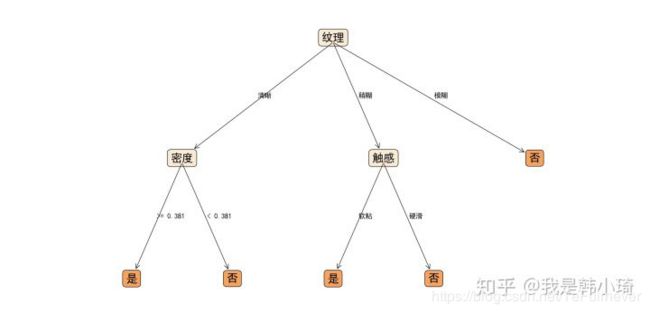
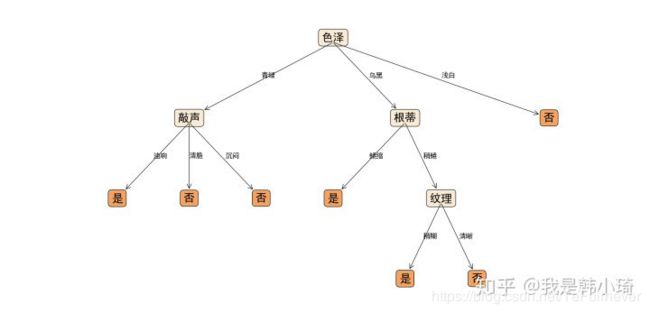
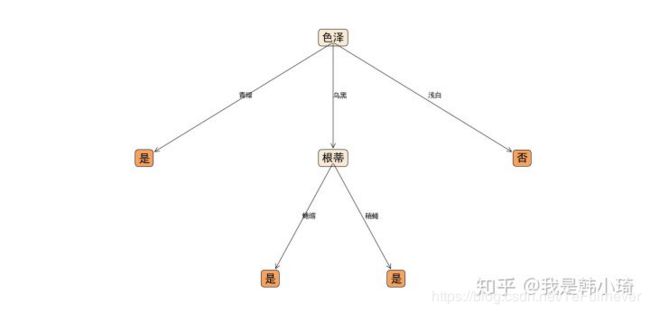
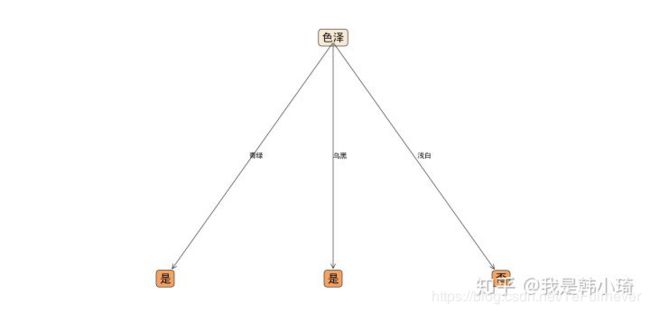
未剪枝、后剪枝、预剪枝生成决策树分别如下：

• 未剪枝
  
• 后剪枝
  
• 预剪枝
  

最近时间不多，暂且挖个坑。

简要的分析一下：

• ID3算法基于信息熵增益，CART算法则采用了基尼系数。两种划分属性选择均是基于数据纯度的角度，方法差距应该不大（CART可能要好一点）。而对率回归进行划分选择，以斜划分的方式，实现了多变量参与划分，其模型决策边界更光滑。
• 相比于决策树的生成算法，剪枝操作更影响模型性能。

主要思路每一次循环遍历一层下节点(除去叶节点)，为每一个节点生成子节点，将非叶节点入队；用参数L保存每一层有多少个节点。下一次循环执行同样的步骤。直至所有的节点都叶节点，此时队列为空。

具体如下：

输入：训练集D = {(x1, y1), (x2, y2)...(xm, ym)};
	  属性集A = {a1, a2... ad};
	  最大深度MaxDepth = maxDepth
	  
过程：函数TreeDenerate(D, A, maxDepth)

1:  生成三个队列，NodeQueue、DataQueue、AQueue分别保存节点、数据、和剩余属性集;
2:  生成节点Node_root;
3:  if A为空 OR D上样本都为同一类别:
4:		将Node_root标记为叶节点，其标记类别为D中样本最多的类;
5: 		return Node_root;
6:  end if 
7:  将Node入队NodeQueue; 将D入队 DataQueue; 将A入队AQueue;
8:  初始化深度depth=0;
9:  初始化L = 1;	# L用于记录每一层有多少非叶节点。
10: while NodeQueue 非空:
11:		L* = 0
12:		for _ in range(L):			# 遍历当前L个非叶节点
13:			NodeQueue 出队Node; DataQueue出队D; AQueue 出队A;
14:			从A中选择一个最优划分属性a*;
15:			for a* 的每一个值 a*v do:
16:				新建一个node*，并将node*连接为Node的一个分支;
17:				令 Dv表示为D中在a*上取值为a*v的样本子集;
18:				if Dv为空:
19:					将node*标记为叶节点，其标记类别为D中样本最多的类;
20:					continue;
21:				end if
22:				if A\{a*}为空 OR Dv上样本都为同一类别 OR depth == maxDepth:
23:					将node*标记为叶节点，其标记类别为Dv中样本最多的类;
24:					continue;
25:				end if 			
26:				将node*入队NodeQueue; 将Dv入队 DataQueue; 将A\{a*} 入队AQueue;
27:				L* += 1;		# 用于计算在第depth+1 层有多少个非叶节点
28:		L = L*;
29:		depth += 1;
30:	return Node_root;
输入以Node_root为根节点的一颗决策树

4.7写的算法就是广度优先搜索的。这道题将MaxDepth改为MaxNode，只需要改几个地方。有一点需要注意的地方，就是在给一个节点生成子节点时（19-32行），可能造成节点数大于最大值的情况，比如某属性下有3种取值，那么至少要生成3个叶节点，这个时候节点总数可能会超过最大值，这时最终节点数可能会是MaxNode+2。

至于两种算法对比。个人理解当数据特征值，各属性的取值较多时，形成的决策树会趋于较宽类型的树，这时使用广度优先搜索更容易控制内存。若属性取值较少时，深度优先搜索更容易控制内存。

对4.7中修改如下：

输入：训练集D = {(x1, y1), (x2, y2)...(xm, ym)};
	  属性集A = {a1, a2... ad};
	  最大深度MaxNode = maxNode
	  
过程：函数TreeDenerate(D, A, maxNode)

1:  生成三个队列，NodeQueue、DataQueue、AQueue分别保存节点、数据、和剩余属性集;
2:  生成节点Node_root;
3:  if A为空 OR D上样本都为同一类别:
4:		将Node_root标记为叶节点，其标记类别为D中样本最多的类;
5: 		return Node_root;
6:  end if 
7:  将Node入队NodeQueue; 将D入队 DataQueue; 将A入队AQueue;
8:  初始化深度numNode=1;
9:  初始化L = 1;	# L用于记录每一层有多少非叶节点。
10: while NodeQueue 非空:
11:		L* = 0
12:		for _ in range(L):			# 遍历当前L个非叶节点
13:			NodeQueue 出队Node; DataQueue出队D; AQueue 出队A;
14:			if numNode >= maxNode:
15:				将Node标记为叶节点，其标记类别为D中样本最多的类;
16:				continue;
17:			end if;
18:			从A中选择一个最优划分属性a*;
19:			for a* 的每一个值 a*v do:
20:				numNode+=1
21:				生成一个node*，并将node*连接为Node的一个分支;
22:				令 Dv表示为D中在a*上取值为a*v的样本子集;
23:				if Dv为空:
24:					将node*标记为叶节点，其标记类别为D中样本最多的类;
25:					continue;
26:				end if
27:				if A\{a*}为空 OR Dv上样本都为同一类别:
28:					将node*标记为叶节点，其标记类别为Dv中样本最多的类;
29:					continue;
30:				end if 			
31:				将node*入队NodeQueue; 将Dv入队 DataQueue; 将A\{a*} 入队AQueue;
32:				L* += 1;		# 用于计算在第depth+1 层有多少个非叶节点
33:			end if;
34:		L = L*;
35:	return Node_root;

讨论：4.7中与4.8中用队列的话均为广度优先搜索，我觉得是出题的时候的疏忽。。

应该是广度优先搜索（队列）+MaxNode控制 与 深度优先搜索（堆栈）+MaxDepth控制 两种方法之间的比较。

个人认为，广度优先搜索（队列）+MaxNode 的方法更容易控制决策树所需内存不溢出。因为最大节点数目是固定的。队列中储存的是当前深度未处理的节点以及当前深度以处理节点的下一级节点，其数目是可控的，总小于最大节点数。而深度优先搜索在堆栈中储存的是当前节点的兄弟节点、当前节点的父节点、当前节点的父节点的兄弟节点…若一些分支节点的分支数很多，那么堆栈的深度就会比较深，虽然有MaxDepth控制最大深度，但还是可能出现栈溢出的情况。

这道题相对简单。使用书中式4.9、4.10、4.11有，对于原书中4.5式可以推广为：

属性a的基尼指数可推广为：

机器学习(周志华) 参考答案 第四章 决策树 4.10

参考文章

• 机器学习（周志华）课后习题
• https://blog.csdn.net/snoopy_yuan/article/category/6788615